博客

1.题目描述

给定一个非空二叉树的根节点

root

, 以数组的形式返回每一层节点的平均值。与实际答案相差

10-5

以内的答案可以被接受。

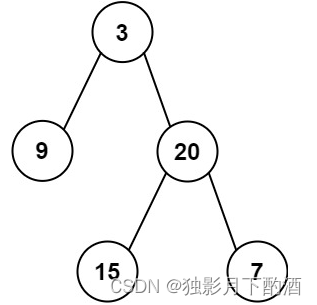
输入：root = [3,9,20,null,null,15,7]

输出：[3.00000,14.50000,11.00000]

解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。

因此返回 [3, 14.5, 11] 。

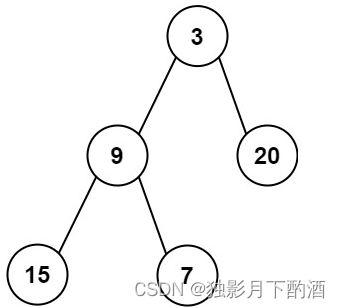
输入：root = [3,9,20,15,7]

输出：[3.00000,14.50000,11.000

提示：

• 树中节点数量在
  
[1, 104]

  范围内
• 
-2^31 <= Node.val <= 2^31 - 1


2.思路分析

2.1 深度优先搜索

1.确定递归函数要处理的参数以及返回值

定义全局变量:totals(存储二叉树每一层的节点值之和)、counts(存储二叉树每一层的节点数)

参数: root(节点)、depth(记录深度)

totals = []
counts = []
def level(root: Optional[TreeNode], depth: int, totals: List[int]) -> None:

2.确定终止条件

当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return

if not root:
    return

3.单层搜索逻辑

if depth < len(totals):
    totals[depth] += root.val
    counts[depth] += 1
else:
    totals.append(root.val) 中
    counts.append(1)

level(root.left, depth + 1) #左
level(root.right, depth + 1) #右

2.2 广度优先搜索

从根节点开始搜索，每一轮遍历同一层的全部节点，计算该层的节点数以及该层的节点值之和，然后计算该层的平均值。

具体做法:

• 初始时，将根节点加入队列；
• 每一轮遍历时，将队列中的节点全部取出，计算这些节点的数量以及它们的节点值之和，并计算这些节点的平均值，然后将这些节点的全部非空子节点加入队列，重复上述操作直到队列为空，遍历结束。

3.代码实现

3.1 深度优先搜索

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        totals = []
        counts = []

        def level(root: Optional[TreeNode], depth: int) -> None:
            if not root:
                return
            if depth < len(totals):
                totals[depth] += root.val
                counts[depth] += 1
            else:
                totals.append(root.val)
                counts.append(1)

            level(root.left, depth + 1)
            level(root.right, depth + 1)

        level(root, 0)
        result = [total / count for total, count in zip(totals, counts)]
        return result

复杂度分析

• 时间复杂度：O(n), 二叉树中节点的个数 。
  • 深度优先搜索需要对每个节点访问一次，对于每个节点，维护两个数组的时间复杂度都是O(1)，因此深度优先搜索的时间复杂度是 O(n)。
  • 遍历结束之后计算每层的平均值的时间复杂度是O(h)，其中 h 是二叉树的高度，任何情况下都满足 h≤n。
    
    因此总时间复杂度是O(n)。
• 空间复杂度：O(n), 其中 nn 是二叉树中的节点个数。空间复杂度取决于两个数组的大小和递归调用的层数，两个数组的大小都等于二叉树的高度，递归调用的层数不会超过二叉树的高度，最坏情况下，二叉树的高度等于节点个数。

3.2 广度优先搜索

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        result = []
        if not root:
            return result

        from collections import deque
        que = deque([root])

        while que:
            sum_ = 0
            size = len(que)
            for _ in range(size):
                cur = que.popleft()
                sum_ += cur.val

                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)

            result.append(float(sum_/size))
        return result

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。
  • 广度优先搜索需要对每个节点访问一次，时间复杂度是 O(n)。
  • 需要对二叉树的每一层计算平均值，时间复杂度是 O(h)，其中 hh 是二叉树的高度，任何情况下都满足h≤n。
    
    因此总时间复杂度是 O(n)。
• 空间复杂度：O(n)，其中 n是二叉树中的节点个数。空间复杂度取决于队列开销，队列中的节点个数不会超过 n。