概述
卡尔曼滤波通过“
预测
”—–“
修正
”的方法,估计过程中的状态值,滤波器估计过程中某一时刻的状态,然后用观测变量来修正预测值。因此可以分为时间更新方程(预测)和测量更新方程(修正)。预测的部分负责前向推算当前状态变量和预测误差协方差矩阵P,以便为下一时刻的值构造先验估计,修正的部分负责将先验估计和当前测量值结合,构造改进的后验估计。
卡尔曼滤波需要用系统模型和测量模型表示
假设有一辆小车,其在t-1时刻的位置为 Pt-1(假设一维,t-1为下标),速度为vt-1 ,控制量为ut(控制加速或减速的加速度值)。那么经过delta t时刻小车的位置P和速度v可由以下公式得出:
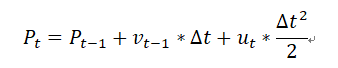
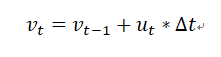
写成矩阵形式即为:
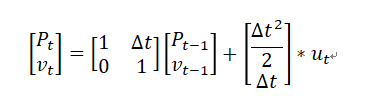
上式加上噪声即为系统模型
因此系统模型为:
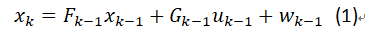
其中x表示状态(位置P和速度v),F称为状态转换矩阵,G称为控制矩阵,w为系统模型噪声分布
测量模型:
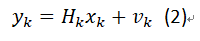
其中H称为观测矩阵,v为测量模型噪声分布
卡尔曼滤波在整体上也可以分成两个部分:预测和修正
预测部分
这部分计算预测值和预测误差协方差矩阵,其中预测值由系统模型得出
计算预测值
:
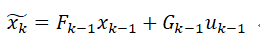
计算预测误差协方差
:
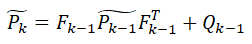
其中的Q为预测系统自带的噪声误差
修正部分
计算最优增益
(卡尔曼系数)
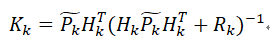
其中R是测量噪声协方差矩阵(由观测模型中的噪声误差v计算得到),可以看出,当测量噪声协方差矩阵趋于0时,卡尔曼系数趋于观测矩阵的逆,此时更偏向于看中观测值。当预测误差协方差趋于0时,卡尔曼系数也趋于0,此时更偏向于预测部分。
计算修正后的预测值
:
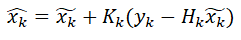
其中y是传感器得到的带有观测误差的观测值。
详细解释一下观测矩阵H的作用
在本例子中修正后的x会得到一个标量值,是因为例子想得到小汽车的位置所以H=[1,0],但如果在观测过程中获得多个传感器的多维度信息,x就会得到一个多维列向量,其中包含了不同传感器测量的测量值,可以从这些不同维度的测量值推断出状态值,这就是数据融合的功能在观测矩阵H上体现出来的。
修正时如何保证对状态中所有的值均进行了更新
前面在算卡尔曼系数时,公式中包含了预测误差协方差P,其实已经利用了位置和速度的在协方差上的相关性,因此只要计算协方差既可以保证对状态上所有维度进行更新。
计算修正后的预测协方差:
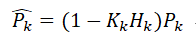
迭代计算以上五个公式,即可得到任意时刻t的状态预测。