决策树

可以看到,决策树的决策过程非常直观,容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支生物学以及商业等诸多领域。知道了决策树的定义以及其应用方法,下面介绍决策树的构造算法。
在决策树算法的学习过程中,
信息增益是特征选择的一个重要指标
,它定义为一个特征能够为分类系统带来多少信息,带来的信息越多,说明该特征越重要,
相应的信息增益也就越大。
概念
我们前面说了,信息熵是代表随机变量的复杂度(不确定度),条件熵代表在某一个条件下,随机变量的复杂度(不确定度)
而我们的
信息增益
恰好是:
信息熵-条件熵。
换句话说,信息增益代表了在一个条件下,信息复杂度(不确定性)减少的程度。
那么我们现在也很好理解了,在决策树算法中,我们的关键就是每次选择一个特征,特征有多个,那么到底按照什么标准来选择哪一个特征。
这个问题就可以用信息增益来度量。
如果选择一个特征后,信息增益最大(信息不确定性减少的程度最大)
,那么我们就
选取这个特征。
例子
我们有如下数据:
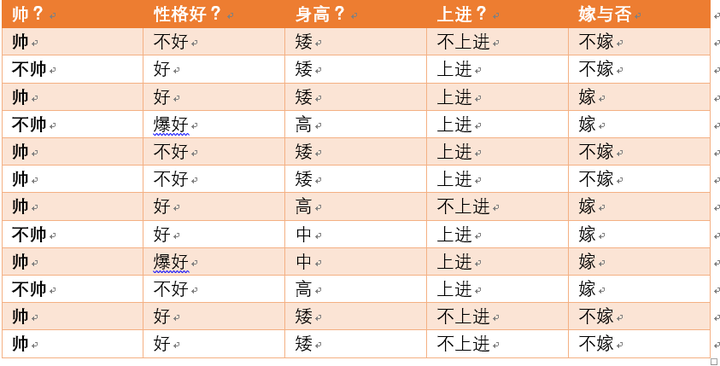
可以求得随机变量X(嫁与不嫁)的信息熵为:
嫁的个数为6个,占1/2,那么信息熵为-1/2log1/2-1/2log1/2 = -log1/2=0.301
现在假如我知道了一个男生的身高信息。
身高有三个可能的取值{矮,中,高}
矮包括{1,2,3,5,6,11,12},嫁的个数为1个,不嫁的个数为6个
中包括{8,9} ,嫁的个数为2个,不嫁的个数为0个
高包括{4,7,10},嫁的个数为3个,不嫁的个数为0个
先回忆一下条件熵的公式如下:
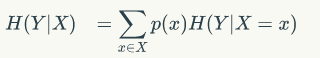
我们先求出公式对应的:
H(Y|X = 矮) = -1/7log1/7-6/7log6/7=0.178
H(Y|X=中) = -1log1-0 = 0
H(Y|X=高) = -1log1-0=0
p(X = 矮) = 7/12,p(X =中) = 2/12,p(X=高) = 3/12
则可以得出条件熵为:
7/12*0.178+2/12*0+3/12*0 = 0.103
那么我们知道信息熵与条件熵相减就是我们的信息增益,为
0.301-0.103=0.198
所以我们可以得出我们在知道了身高这个信息之后,信息增益是0.198
结论
我们可以知道,本来如果我对一个男生什么都不知道的话,
作为他的女朋友决定是否嫁给他的不确定性有0.301这么大。
当我们知道男朋友的身高信息后,不确定度减少了0.198.也就是说,
身高这个特征对于我们广大女生同学来说,决定嫁不嫁给自己的男朋友是很重要的。
至少我们知道了身高特征后,我们原来没有底的心里(0.301)已经明朗一半多了,减少0.198了(大于原来的一半了)。
那么这就类似于非诚勿扰节目里面的桥段了,请问女嘉宾,你只能知道男生的一个特征。请问你想知道哪个特征。
假如其它特征我也全算了,
信息增益是身高这个特征最大
。
那么我就可以说,孟非哥哥,我想知道男嘉宾的一个特征是身高特征。因为它在这些特征中,对于我挑夫君是最重要的,信息增益是最大的,知道了这个特征,嫁与不嫁的不确定度减少的是最多的。
建立决策树主要有三种算法
- ID3 :适应信息增益来进行特征选择的决策树学习过程
- C4.5:信息增益率
- CART:基尼指数
总结:一个属性的信息增益越大,表明属性对样本的熵减少的能力越强,这个属性使得数据由不确定性变成确定性的能力越强
投票机制
1. 一票否决
2. 少数服从多数
3. 贝叶斯投票机制:
基于每个基本分类器在过去的分类表现设定一个权值,然后按照这个权值进行投票