文章目录
前言
本篇为大创团队的第五篇集体作品,针对物理光学的基础实验–泊松亮斑做出了探索和尝试。
一、泊松亮斑实验原理简介
1、现象
当单色光照射在直径恰当的小圆板或圆珠时,会在之后的光屏上出现环状的互为同心圆的衍射条纹,并且在所有同心圆的圆心处会出现一个极小的亮斑,这个亮斑就被称为泊松亮斑。

2、半波带理论
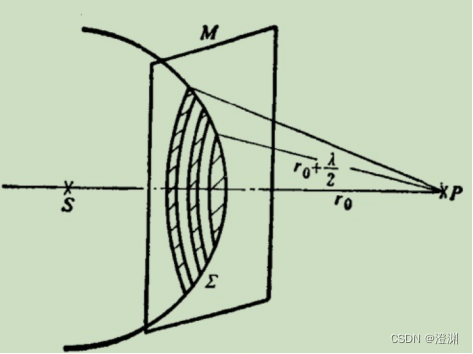
即观测点P为中心,作半径为
r
0
r_0
r
0
的一系列球面,这些球面与衍射屏的交汇便是如图所示一系列圆环。
当
r
0
≫
λ
r_0\gg\lambda
r
0
≫
λ
,这些圆环面积相等。P点的振幅就可以看作光透过多少个波带到达了P点,这些波带在P点产生振幅的叠加即是P点的振幅强度。由于每个波带的面积相等,那么每个波带最终到达P点的振幅大小就取决于它们之间的距离了。因为相邻波带到P点的距离皆相差
λ
2
\frac{\lambda}{2}
2
λ
,相邻波带到达P点的相位相差
π
\pi
π
,相邻波带到达P点的振幅的符号不同(一正一负)。
3、公式
E
=
{
∣
E
1
∣
2
+
∣
E
0
∣
2
(
n
为
奇
数
)
∣
E
1
∣
2
+
∣
E
n
−
1
∣
2
−
∣
E
n
∣
(
n
为
偶
数
)
E=\left\{ \begin{aligned} \frac{\vert E_1\vert }{2} +& \frac{\vert E_0\vert }{2} &(n为奇数)&\\ \frac{\vert E_1\vert }{2} + &\frac{\vert E_{n-1}\vert }{2}-\vert E_n\vert &(n为偶数)& \end{aligned} \right.
E
=
⎩
⎪
⎪
⎨
⎪
⎪
⎧
2
∣
E
1
∣
+
2
∣
E
1
∣
+
2
∣
E
0
∣
2
∣
E
n
−
1
∣
−
∣
E
n
∣
(
n
为
奇
数
)
(
n
为
偶
数
)
n
→
∞
,
∣
E
n
∣
=
0
,
∣
E
n
−
1
∣
=
0
n\rarr\infin,\vert E_n\vert=0,\vert E_{n-1}\vert=0
n
→
∞
,
∣
E
n
∣
=
0
,
∣
E
n
−
1
∣
=
0
因此可见圆屏衍射永远是一个亮斑,而且P点的总振幅为第一个波带在P点产生振幅的一半。
二、Virtualab仿真
1、搭建光路
首先在面板中拖入一个高斯波,双击设置其属性:
其中可以选择厄米高斯波或者拉盖尔高斯波,拉盖尔高斯光用柱坐标表示,具有方位角相位,有确定的轨道角动量,拉盖尔高斯光与介质相互作用时会将其轨道角动量传递给介质,而厄米高斯光用直角坐标表示(在实验中未设阶次order所以更换模式表现出来的结果差异不大,默认即可)
而本实验选择默认的厄米特高斯波,并且设置其束腰半径为100um×100um,束腰半径的设置可以同时改变半发散角和瑞利长度(这三个量互相关联变化)。
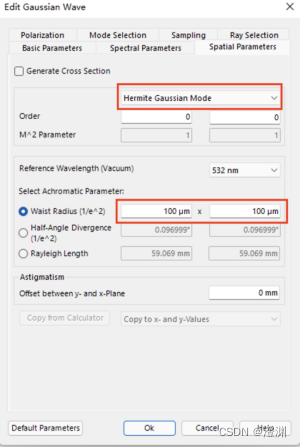
设置高斯波波长为532nm的绿光
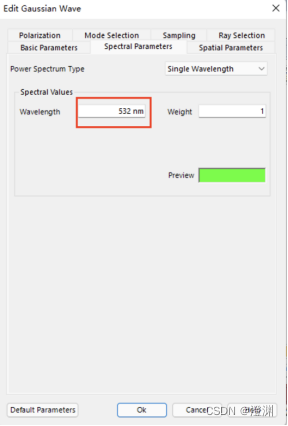
其后在面板中拖入圆屏:在库中找到stop拖入。
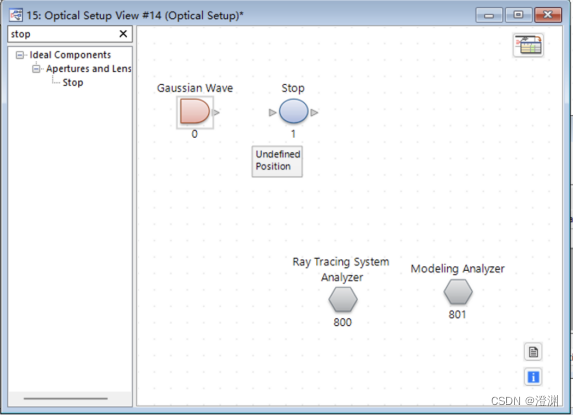
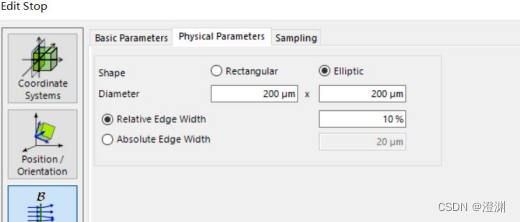
双击设置其属性形状为椭圆形,设置其大小为100um×100um的圆形。
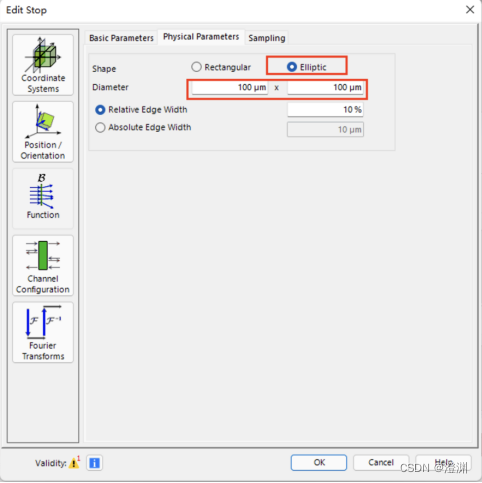
其后拖入两个探测器分别探测一维、二维图像,两探测器都位于圆板后2mm位置。
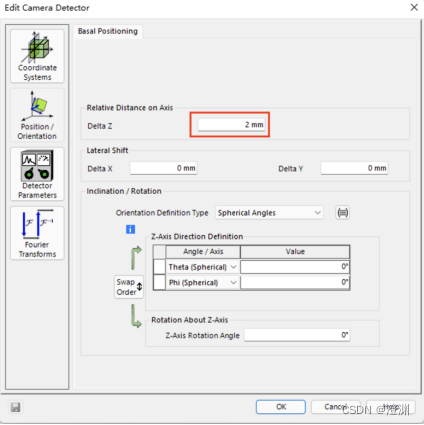
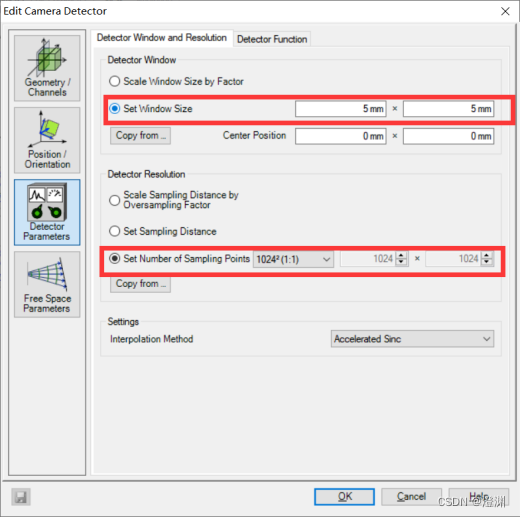
由于camera detector的像素需要尽可能符合现实情况中CCD或的探测器,因此我们将2D探测器的探测窗口大小设置为1.28×1.28mm,
采样点设为256×256
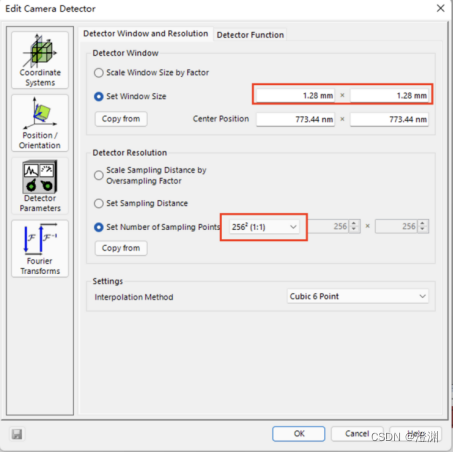
1D探测器的探测窗口大小设置为1.28mm×5um,采样点改为自定义设置为256×1
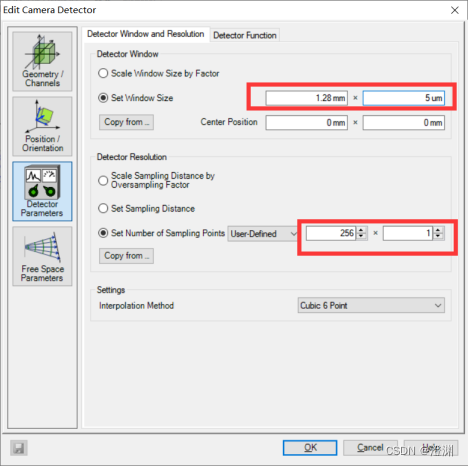
值得注意的是,2013版本中需要选择2代场追迹,试用版中经典场追迹即可。
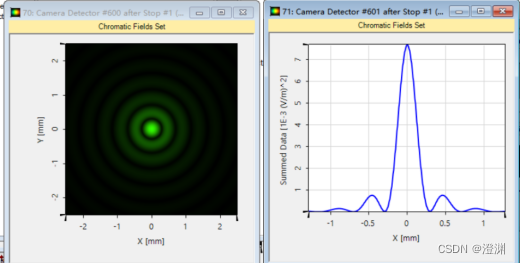
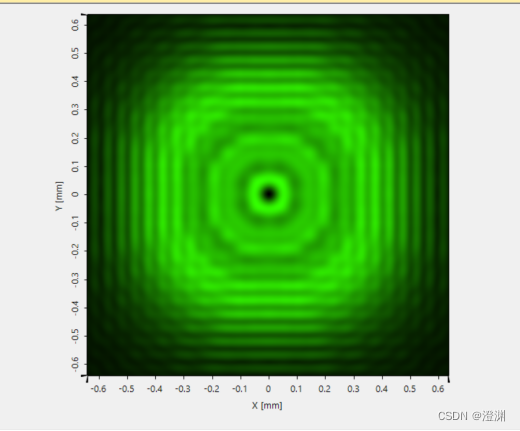
至此可得到泊松亮斑的图像和一维光强分布曲线:
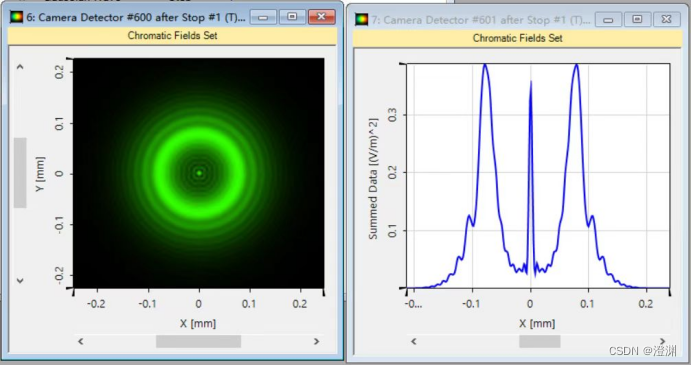
2、探测器窗口大小确定
对于探测器窗口大小的确定,可以使用光线追迹的功能得到点列图
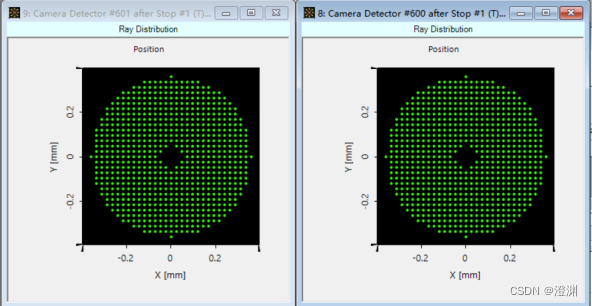
此后需要在上方选择Show Rectangle or Ellipse Marker来激活窗口。
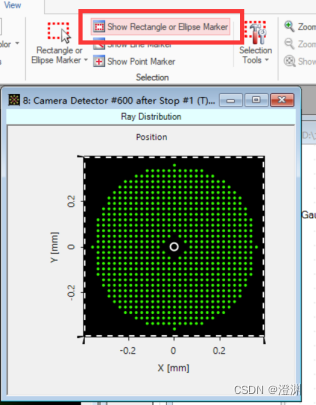
激活后可在探测器中导入,这时探测器中窗口大小会自动更改。
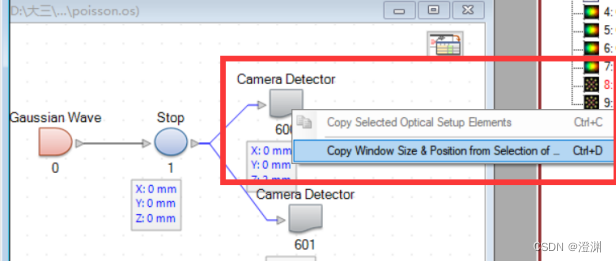
至此基本部分结束。
三、结果展示
1、改变圆屏半径
将圆屏半径分别设为50um,100um和200um。
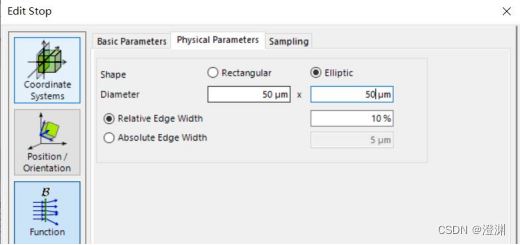
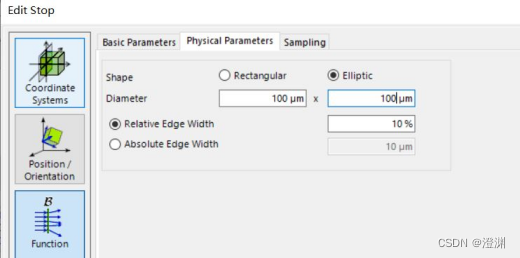
运行三个参数仿真后可以得到如下的仿真结果图像。
注意,这里试用版是可以观察到1D探测器的纵深场的。在这里设置。
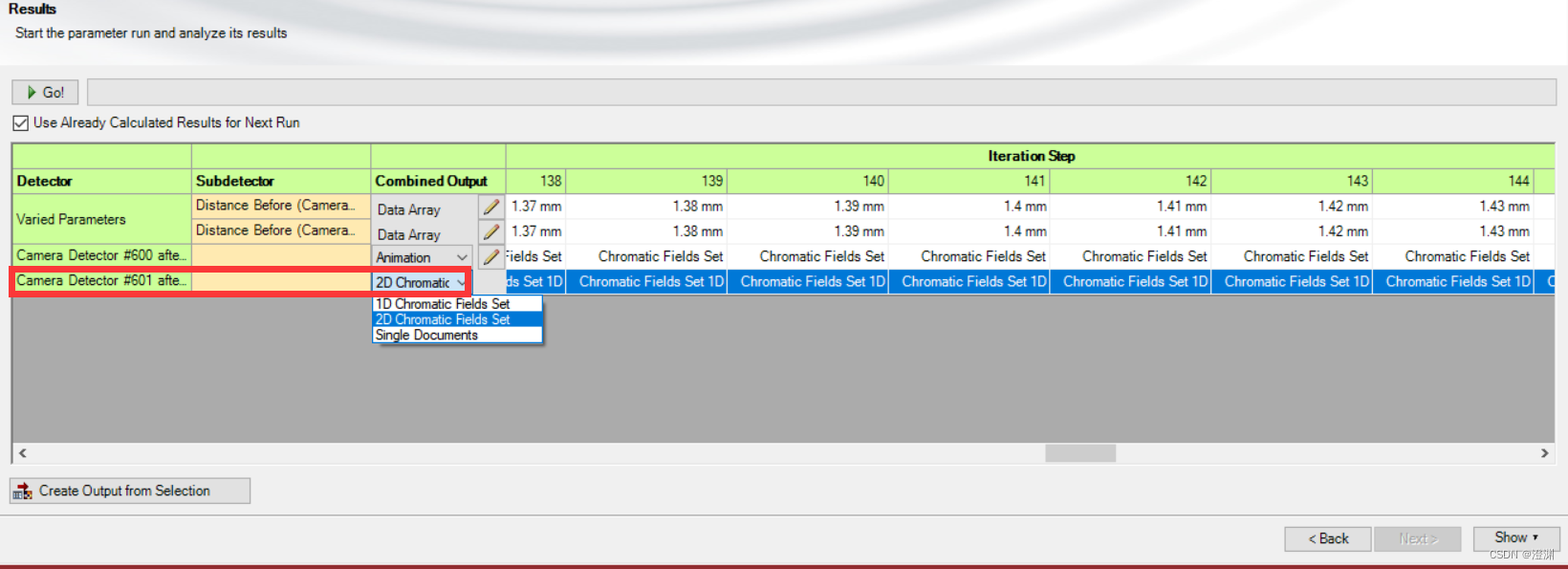
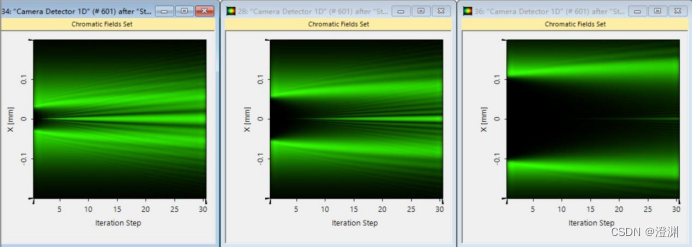
可以看到圆屏半径越大,深度也就越深。圆屏越大,半波带个数越少,对应的亮度也越暗,呈现在图像上即表现为暗部的深度越深。
具体用光强查看。
断开上一个探测器,直接接另一个探测器测量高斯光束中心的光强。
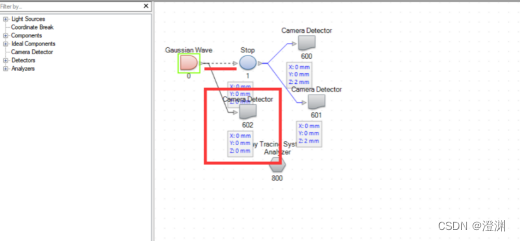
大致是1(V/m)^2。
恢复原光路。
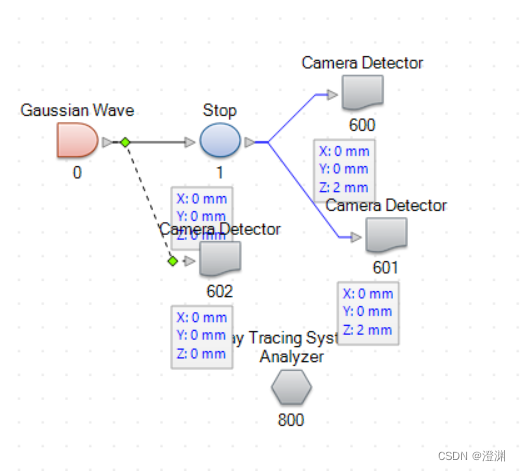
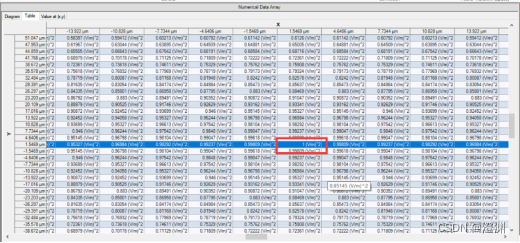
一维探测器的现实中,2mm处圆屏的光强为0.35(V/m)^2,此时圆屏大小为100um。
若采用200um直径大小的圆屏,在2mm处观察圆屏的光强非常弱,需要进一步转化以相对准确地读数
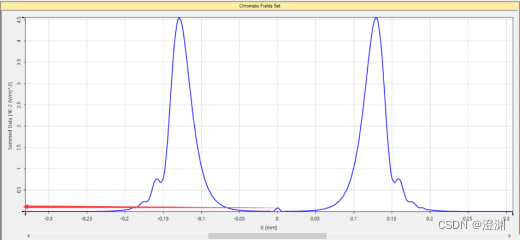
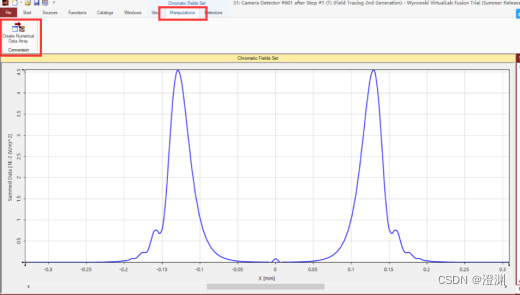
为0.00081638(v/m)^2。
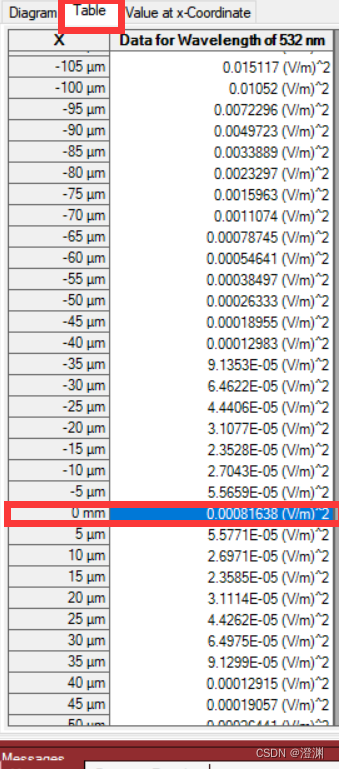
若采用50um直径大小的圆屏,在2mm处观察圆屏的光强很强,也需要进一步转化以相对准确地读数,为0.83257(v/m)^2
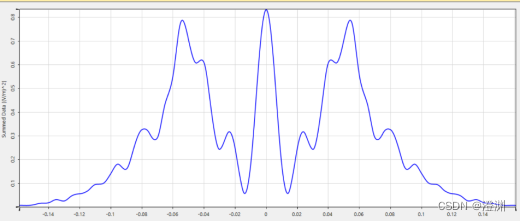
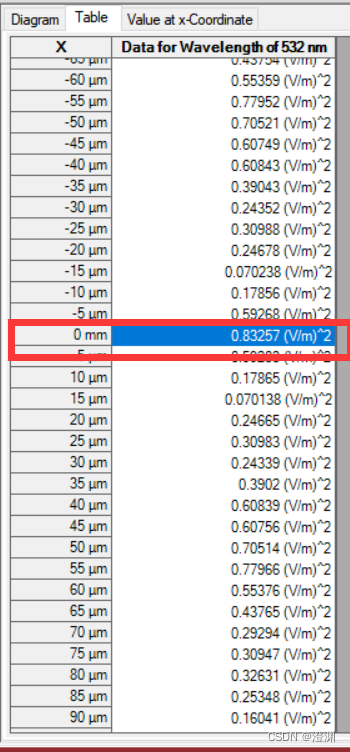
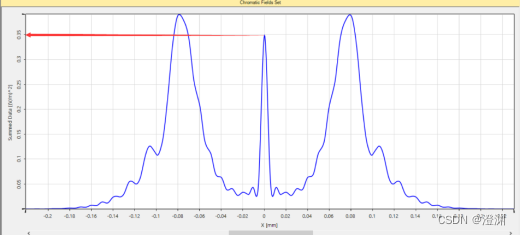
对于2mm处的圆屏虽然没有很明显的亮斑,但随着距离的增加,亮斑的强度也会逐渐增加,如图蓝线代表探测器在2mm处,红线代表在10mm,绿线代表在20mm。
2、改变探测器位置
使用parameter run功能,同时改变两个探测器的位置,从1um到2mm变化。
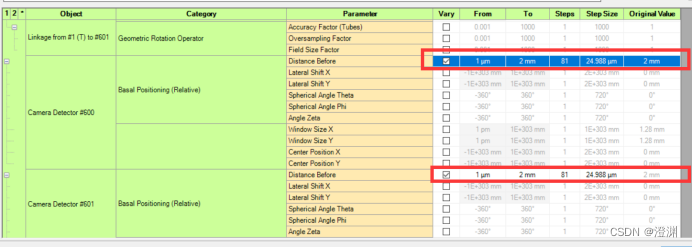
可以得到如下的动态效果图。

衍射结果为一套亮暗相间的同心圆环,当探测器沿轴向移动时,从没有亮斑到有亮斑。
以200mm圆屏为例对于2mm处的圆屏虽然没有很明显的亮斑,但随着距离的增加,亮斑的强度也会逐渐增加,如图蓝线代表探测器在2mm处,红线代表在10mm,绿线代表在20mm。
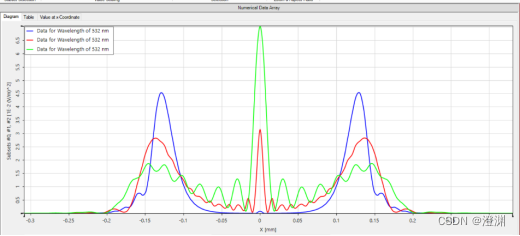
而当200mm的圆屏拉远到50mm处、100mm处、200mm处,中心的光强又开始下降,到红线的时候,曲线非常近似为圆孔的夫琅和费衍射曲线。
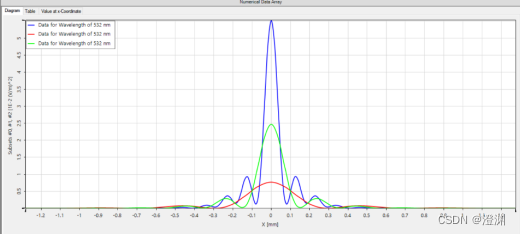
主要改大探测器窗口的大小,此时不只研究中央亮斑,旁边的衍射级次也成为了研究对象
可以看到200mm时曲线和条纹纹样都非常像圆孔夫琅和费衍射时的场景。
3、改变波长
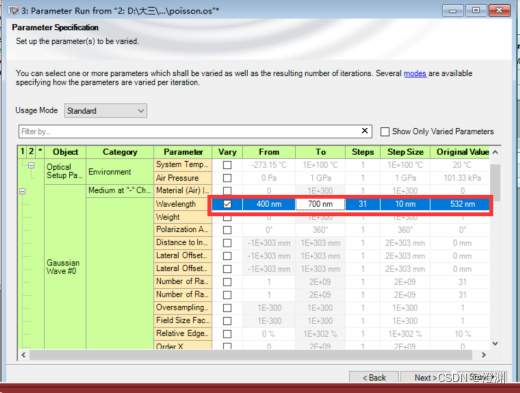

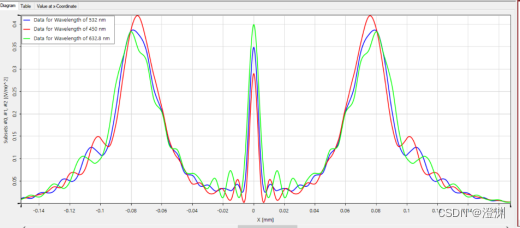
(这张图的配色没有选好,以图例为准,外围衍射条纹遵循了夫琅和费衍射的规律,波长大的中央稍宽,但不明显)
4、圆孔衍射
如果我们考察圆孔衍射,相应的整个光路搭建如下。
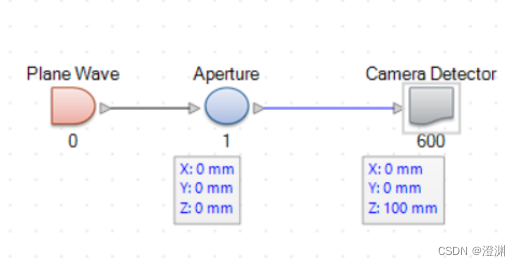
相应的设置如下。
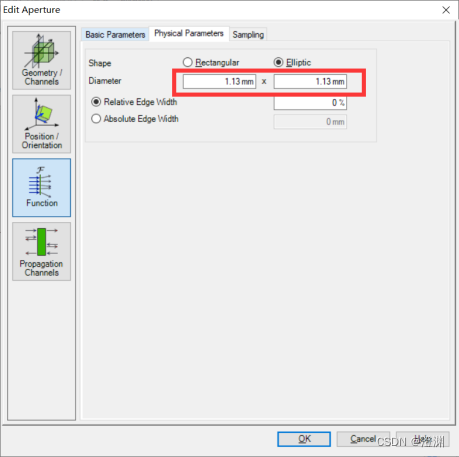
波长为532nm。圆孔直径为1.13mm,根据菲涅尔半波带的计算公式
10
0
2
+
(
1.13
/
2
)
2
−
100
=
n
∗
532
∗
1
0
−
6
2
\sqrt{100^2+(1.13/2)^2}-100=n*\frac{532*10^{-6}}{2}
1
0
0
2
+
(
1
.
1
3
/
2
)
2
−
1
0
0
=
n
∗
2
5
3
2
∗
1
0
−
6
,计算可得,n=6,即有6个半波带(偶数),因此,图像中心为暗点。
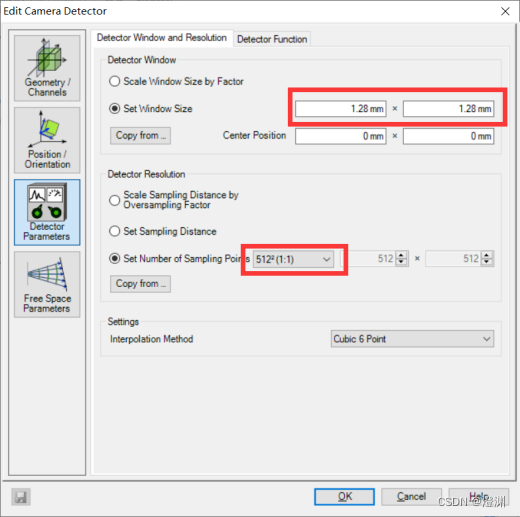
探测器也可以发挥仿真软件的优势设置的更细致些。
用classic field tracing仿真。(类比单缝夫琅和费衍射)
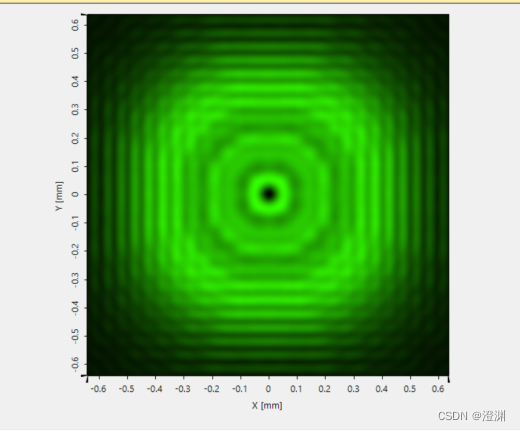
转换成数值模式。
查看曲线。
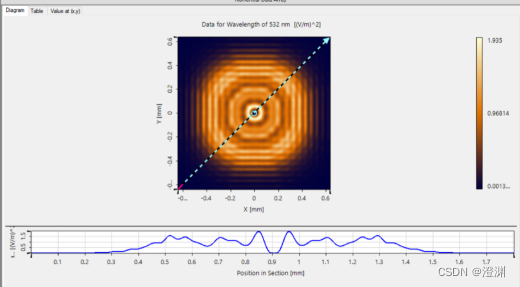
这时因为光阑允许6个半波带透过,衍射场中心为暗点。
改变光阑的直径。
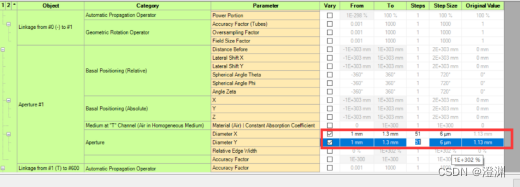
得到亮暗交替的变化。

改变探测器的距离。
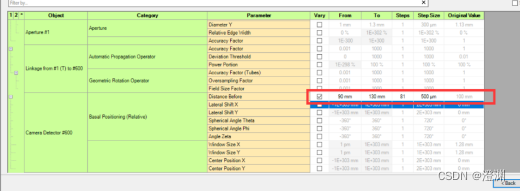
有一样的效果。

5、巴比涅原理的一点说明
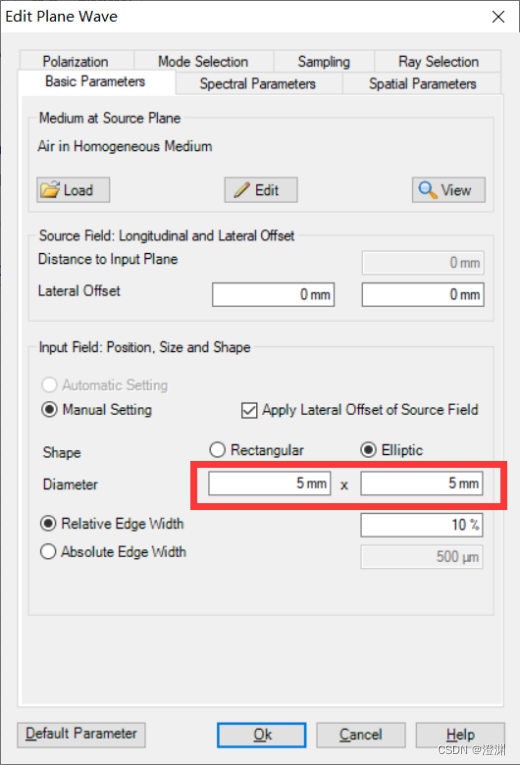
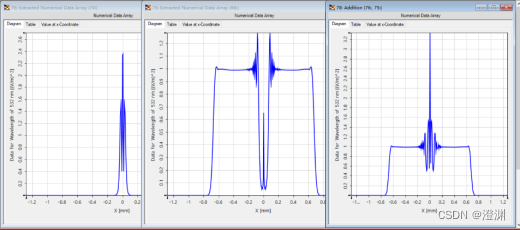
把stop换成与它同样大小的圆孔(用平面波做光源照射统一变量)。叠加圆屏衍射与圆孔衍射的图可以看到最后的差异基本在近轴区域或者说是轴上点,其余位置有一样的光强。
四、关于高斯光束里的模式

在这里设置。(平常是00的话就只有基模)
厄密高斯光束出来结果是方的。

拉盖尔高斯光束出来结果是圆的。

总结
本篇由大创团队成员:唐艺恒、扶杨玉、黄一诺、李思潼、明玥共同完成。
本篇采用市面上流通比较广的试用版和7.6.1.18版本进行实验和演示,增强了适用性。
泊松亮斑以及近场圆孔衍射是衍射理论中的另外重要一part,菲涅尔衍射,也非常有意义。