-
1.算法描述
批量梯度下降
的主要问题是它
要用整个训练集来计算每一步的梯度
,训练集大时算法特别慢。相反,
随机梯度下降
,
每一步在训练集中随机选择一个实例,并且仅基于该单个实例来计算梯度
。

与使用批量梯度下降相比,随机梯度下降时,每个训练步骤要快得多,但也更加随机
当成本函数非常不规则时,随机梯度下降可以帮助算法跳出局部最小值,所以相比批量梯度下降,它对于
找全局最小值更有优势
因此随机性的好处是可以
逃离局部最优
,但是缺点是
永远定位不出最小值
-
2. 实验模拟
开始的时候步长较大,这有助于快速进展和逃离局部最小值,然后越来越小,让算法尽可能靠近全局最小值—
模拟退火
每个迭代学习率的函数的叫学习调度。如果学习率下降得太快,可能会陷入局部最小值,甚至是停留在走向最小值的半途中。如果学习率降得太慢,需要太长时间才能跳到差不多最小值附近,如果提早结束训练,可能只得到一个次优解的方案
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
X=2*np.random.rand(100,1)
X=np.matrix(X)
y=4 + 3*X + np.random.rand(100,1)
y=np.matrix(y)
n_epochs=50
t0,t1=5,50
def learning_schedule(t):
return t0/(t+t1)
def picture(X_new,y_predict):
plt.plot(X_new,y_predict,"r-")
plt.plot(X,y,"b.")
X_b=np.c_[np.ones((100, 1)), X]
theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
X_new=np.array([[0],[2]])
X_new_b=np.c_[np.ones((2,1)),X_new]
n_iterations=1000#迭代次数
m=100
theta=np.random.randn(2,1)
for epoch in range(n_epochs):
for i in range(m):
random_index=np.random.randint(m)
xi=X_b[random_index:random_index+1]
yi=y[random_index:random_index+1]
gradients=2*xi.T.dot(xi.dot(theta)-yi)
eta=learning_schedule(epoch*m+i)#learning rate
theta=theta-eta*gradients
y_predict = X_new_b.dot(theta)
picture(X_new, y_predict)
print(theta)
plt.axis([0,2,0,15])
plt.xlabel('X1')
plt.ylabel('y')
plt.show()虽然批量梯度下降代码在整个训练集中进行了1000次迭代,但此代码仅在训练集中遍历了50次,并达到了一个很好的解决方案
[[4.46409376]
[3.03674864]]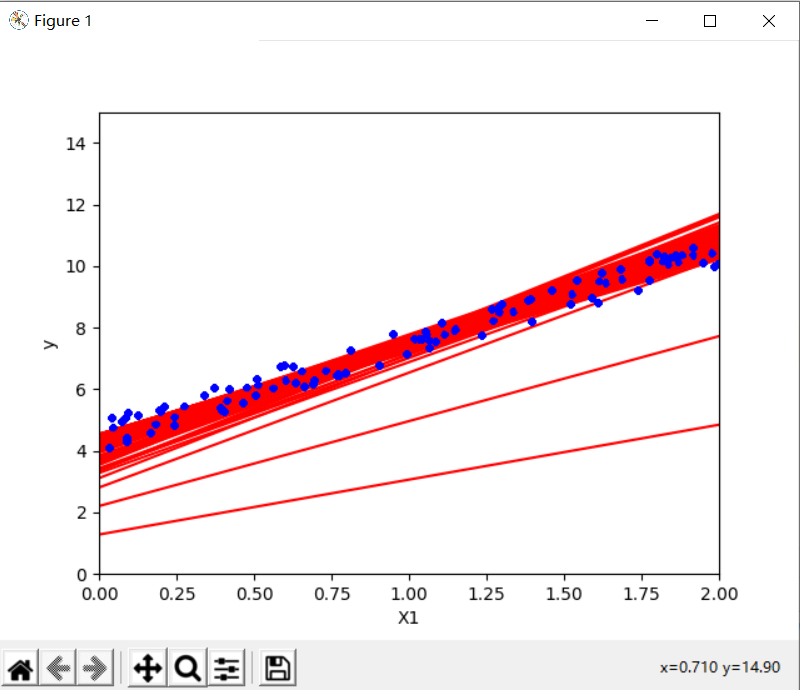
-
3. 注意事项
使用随机梯度下降时,训练实例必须独立同分布,以确保平均而言将参数拉向全局最优值
,其中的实例是随机选取的,因此某些实例可能每个轮次中被选取几次,而其他实例则可能根本不被选取,解决方法为
混洗—遍历—混洗
,但是,这种方法通常收敛较慢
-
4. 使用Scikit—Learn的随机梯度下降执行线性回归
使用SGDRegressor类,该类默认优化平方误差成本函数
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
X=2*np.random.rand(100,1)
X=np.matrix(X)
y=4 + 3*X + np.random.rand(100,1)
y=np.matrix(y)
#这是由于在新版的sklearn中,所有的数据都应该是二维矩阵,哪怕它只是单独一行或一列
#(比如前面做预测时,仅仅只用了一个样本数据),所以需要使用.reshape(1,-1)进行转换
y = np.array(y).reshape(1, -1)
from sklearn.linear_model import SGDRegressor
#1.代码最多可以执行1000次
#2.或者直到一个轮次期间损失下降小于0.001为止
#4.默认学习调度以0.1的学习率开始
sgd_reg=SGDRegressor(max_iter=1000,tol=1e-3,penalty=None,eta0=0.1)
sgd_reg.fit(X,y.ravel())
print(sgd_reg.intercept_,sgd_reg.coef_)再次找到了一种非常接近于由标准方程返回的解
[4.46581072] [3.00165571]