概述
有了平衡二叉树为什么要红黑树
虽然平衡树解决了二叉查找树退化为近似链表的缺点,能够把查找时间控制在O(logn),不过却不是最佳的,因为平衡树要求每个节点的左子树和右子树的高度差至多等于1,这个要求实在是太严了,导致每次进行插入/删除节点的时候,几乎都会破坏平衡树的第二个规则,进而我们都需要通过左旋和右旋来进行调整,使之再次成为一颗符合要求的平衡树。
红黑树
一棵红黑树是满足下面
红黑性质
的二叉搜索树:
-
每个结点或是红色的,或是黑色的。
-
根结点是黑色的。
-
每个叶结点(NIL)是黑色的。
(叶子结点实际上是空结点) -
如果一个结点是红色的,则它的两个子结点都是黑色的。
(所以不可能两个红结点相连) -
对每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
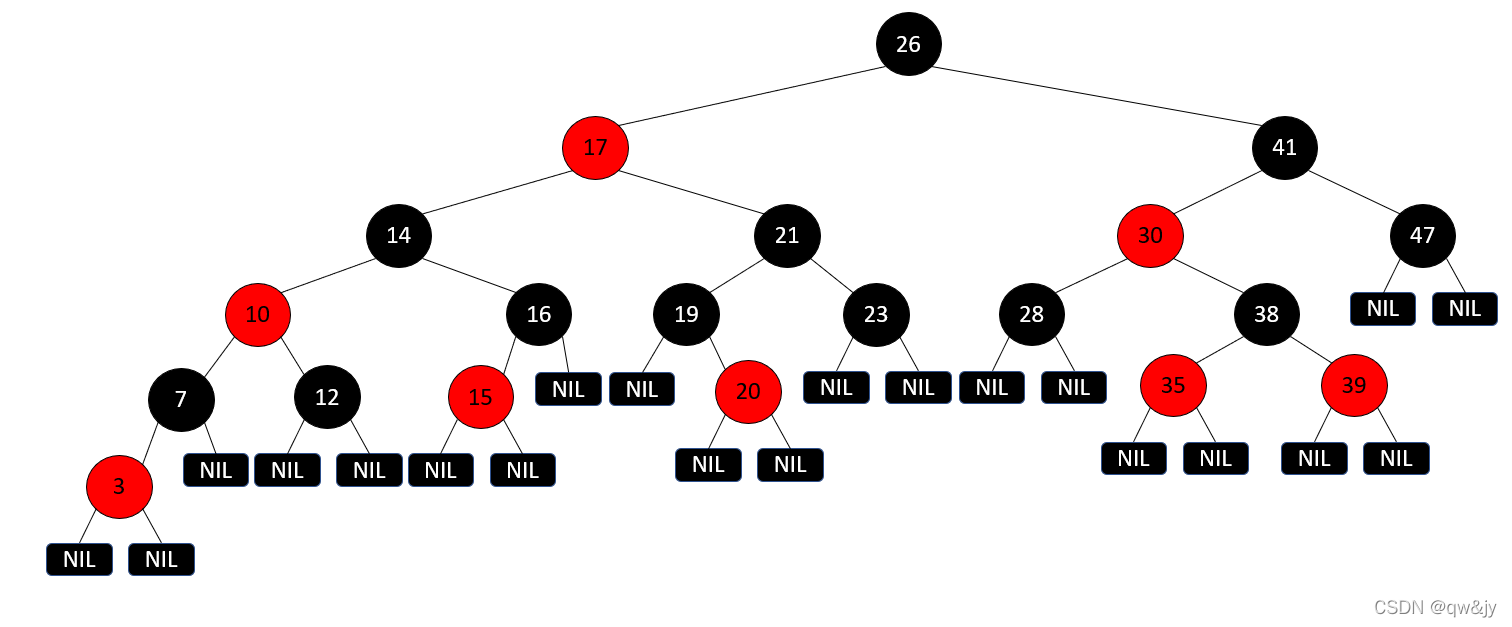
红黑树性质
一棵有 n 个内部结点的红黑树的高度至多为 2lg(n+1)。
从某个结点 x 出发(不含该结点)到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的
黑高
,记为 bh(x)。
证明
:先证以任一结点 x 为根的子树中至少包含 2
bh(x)
-1 个内部结点。如果 x 的高度为 0,则 x 必为叶结点,且以 x 为根结点的子树至少包含 2
bh(x)
-1 = 2
0
-1 = 0 个内部结点。考虑一个高度为正值且有两个子结点的内部结点 x。每个子结点有黑高 bh(x) 或 bh(x)-1,其分别取决于自身的颜色是红还是黑。由于 x 子结点的高度比 x 本身的高度要低,可以利用归纳假设得出每个子结点至少有 2
bh(x)
-1 个内部结点的结论。于是,以 x 为根的子树至少包含(2
bh(x)-1
-1) + (2
bh(x)-1
-1) + 1 = 2
bh(x)
-1 个内部结点,因此得证。
设 h 为树得高度。根据性质 4,从根到叶结点(不包括根结点)的任何一条简单路径上都至少有一半的结点为黑色。因此,根的黑高至少为 h/2;于是有 n≥2
h/2
-1,变换得到 lg(n+1)≥h/2,即 h≤2lg(n+1)。
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
应用
-
Linux非实时任务调度中的应用
Linux 的稳定内核版本在 2. 6. 24 之后,使用了新的调度程序 CFS,所有非实时可运行进程都以虚拟运行时间为 key 值挂在一棵红黑树上,以完成更公平高效地调度所有任务。CFS 弃用 active /expired 数组和动态计算优先级,不再跟踪任务的睡眠时间和区别是否交互任务,并且在调度中采用基于时间计算键值的红黑树来选取下一个任务,根据所有任务占用 CPU 时间的状态来确定调度任务优先级。 -
Linux虚拟内存中的应用
32 位 Linux 内核虚拟地址空间划分 0 - 3G 为用户空间,3 - 4G 为内核空间,因此每个进程可以使用 4GB的虚拟空间。同时,Linux 定义了虚拟存储区域( VMA) 以便于更好表示进程所使用的虚拟空间,每个 VMA是某个进程的一段连续虚拟空间,其中的单元具有相同的特征,所有的虚拟区域按照地址排序由指针链接为一个链表。当发生缺页中断时搜索 VMA 到指定区域时,则需要频繁操作,因此选用了红黑树以减少查找时间。 -
检测树的平衡性上的应用
红黑树是一种自平衡二叉搜索树,它的每个结点都被“着色”为红色或者黑色,这些结点的颜色被用来检测树的平衡性。红黑树作为嵌入式数据库中的索引机制,可以获得更好的性能,对于SQLite数据库,可以采用红黑树实现索引机制的优化。
旋转
左旋和右旋
。当在某个结点 x 上做左旋时,假设它的右孩子为 y 而不是叶结点;x 可以为其右孩子不是叶结点的树内任意结点。左旋以 x 到 y 的链为“支轴”进行。它使 y 成为该子树新的根结点,x 成为 y 的左孩子,y 的左孩子成为 x 的右孩子。
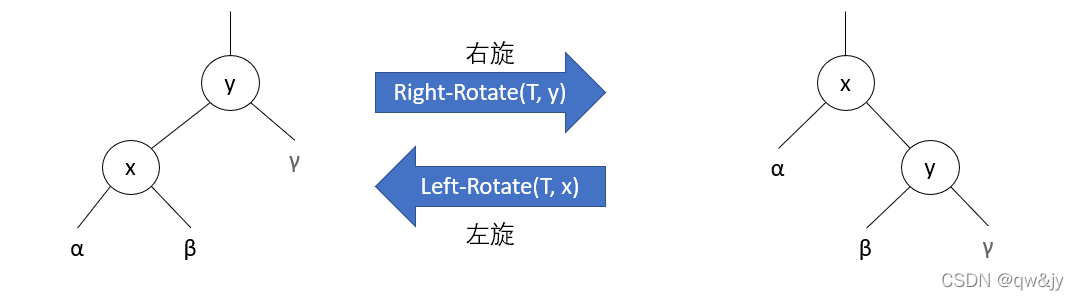
二叉搜索树上的旋转操作。操作 Left-Rotate(T, x) 通过改变常数数目的指针,可以将右边两个结点的结构转变成左边的结构。左边的结构可以使用相反的操作 Right-Rotate(T, y) 来转变成右边的结构。字母 α、β 和 γ 代表任意的子树。旋转操作保持了二叉搜索树的性质:α 的关键字在 x.key 之前,x.key 在 β 的关键字之前,β 的关键字在 y.key 之前,y.key 在 γ 的关键字之前。
左旋
void Left_Rotate(BiTree x){//左旋
if(x != NULL){
BiTree y = x->right;
x->right = y->left;//左旋后,x的右子树变成y的左孩子
if(y->left != NULL)
y->left->parent = x;//β确认父亲为x
y->parent = x->parent;//认x的父亲为爹
if(x->parent == NULL)//若x无父亲,那y就是树的根结点
root = y;
else if(x->parent->left == x)//若x有父亲并且是它父亲的左孩子,x的父亲认y为左孩子,x丢弃
x->parent->left = y;
else//若x有父亲并且是它父亲的右孩子,x父亲认y为右孩子,丢弃x
x->parent->right = y;
y->left = x;//x成为y的左孩子
x->parent = y;
}
}
右旋
void Right_Rotate(BiTree y){//右旋
if(y != NULL){
BiTree x = y->left;
y->left = x->right;//右旋后,y的左子树变成x的右孩子
if(x->right != NULL)
x->right->parent = y;//x的右孩子确认y为父亲
x->parent = y->parent;//认y的父亲为爹
if(y->parent == NULL)//若y无父亲,那x就是树的根结点
root = x;
else if(y->parent->right == y)//若y有父亲并且是它父亲的右孩子,y的父亲认x为右孩子,丢弃y
y->parent->right = x;
else//若y有父亲并且是它父亲的左孩子,y的父亲认x为左孩子,丢弃y
y->parent->left = x;
x->right = y;//y变成x的右孩子
y->parent = x;
}
}
插入
插入分为两步:
-
首先和
二叉排序树
的插入—样,查找、插入 - 调整结构,以保证满足红黑树性质:①对结点重新着色;②对树进行旋转
插入情况:(插入结点都是红色的)
-
被插入的结点是根结点
直接把此结点涂为黑色。(即树原本是空树,插入一个) -
被插入的结点的父结点是黑色
不需要操作。 -
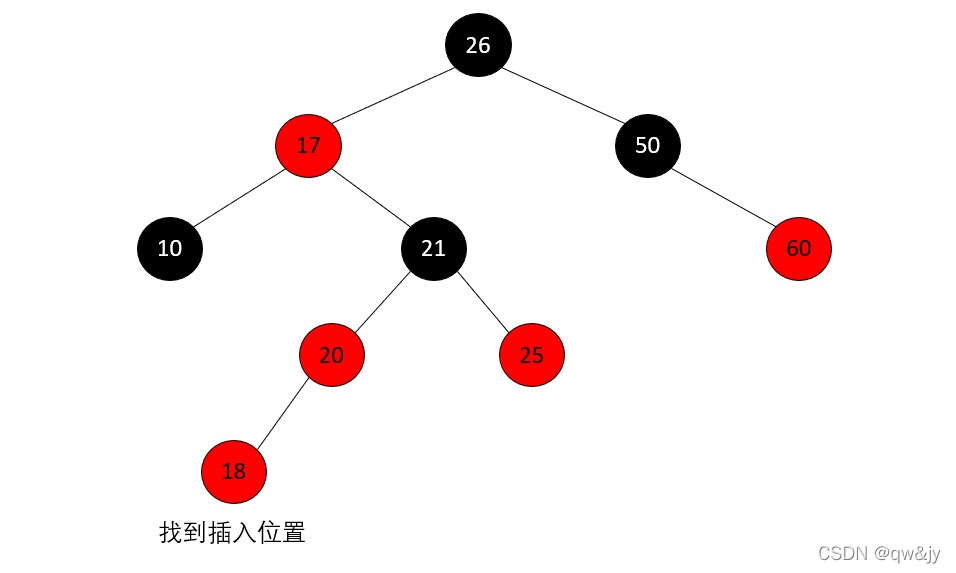
被插入的结点的父结点是红色
[1] 当前结点是祖父结点的另一个子结点(叔叔结点)也是红色。
① 将“父结点”设为黑色。
② 将“叔叔结点”设为黑色。
③ 将“祖父结点”设为红色。
④ 将“祖父结点”设为“当前结点”(红色结点);即,之后继续对“当前结点”进行操作。
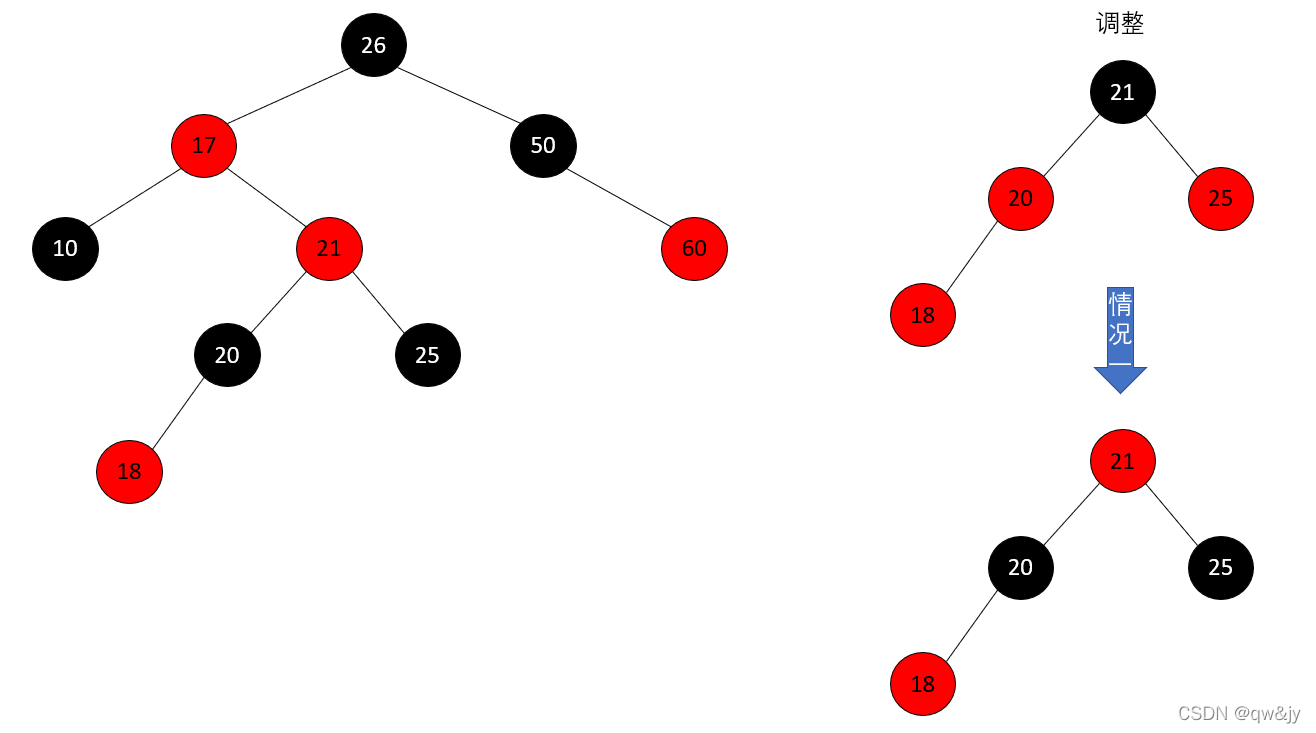
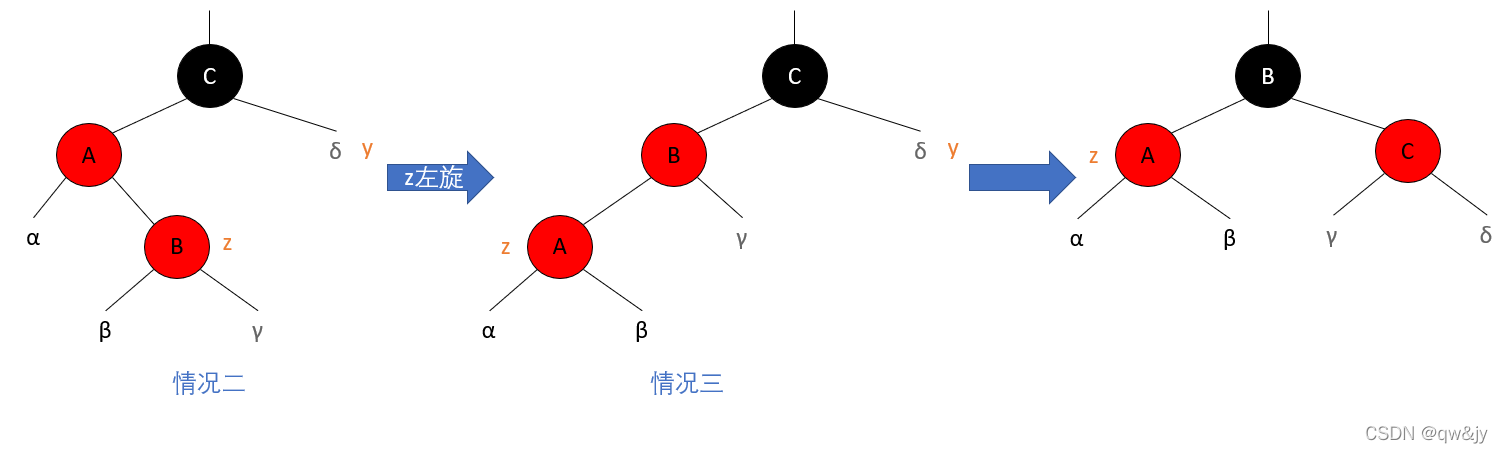
[2] 叔叔结点是黑色,且当前结点是其父结点的右孩子。
① 将“父结点”作为“新的当前结点”。
② 以“新的当前结点”为支点进行左旋。
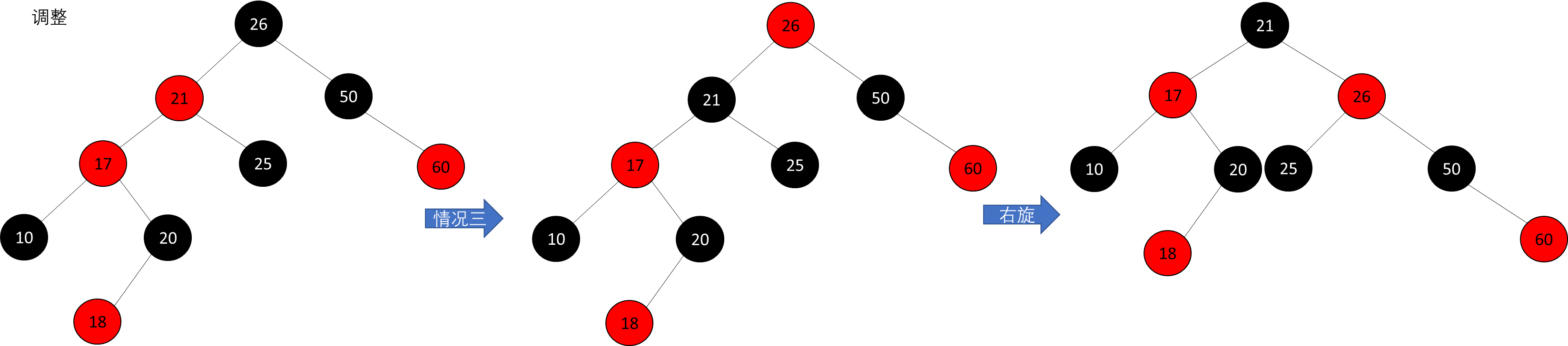
[3] 叔叔结点是黑色,且当前结点是其父结点的左孩子。
① 将“父结点”设为黑色。
② 将“祖父结点”设为红色。
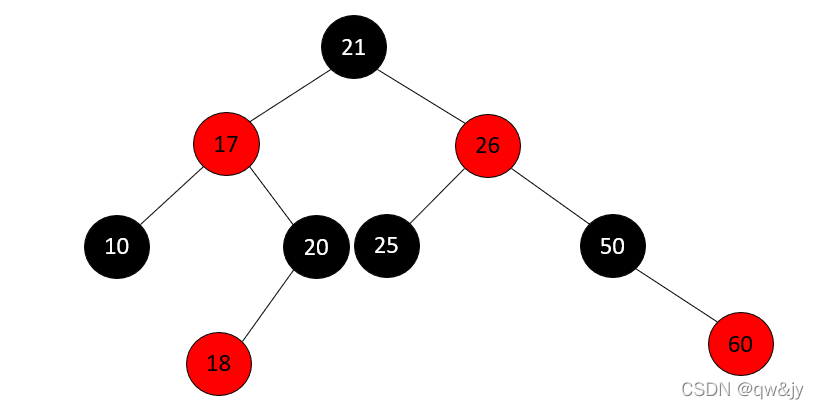
③ 以“祖父结点”为支点进行右旋。
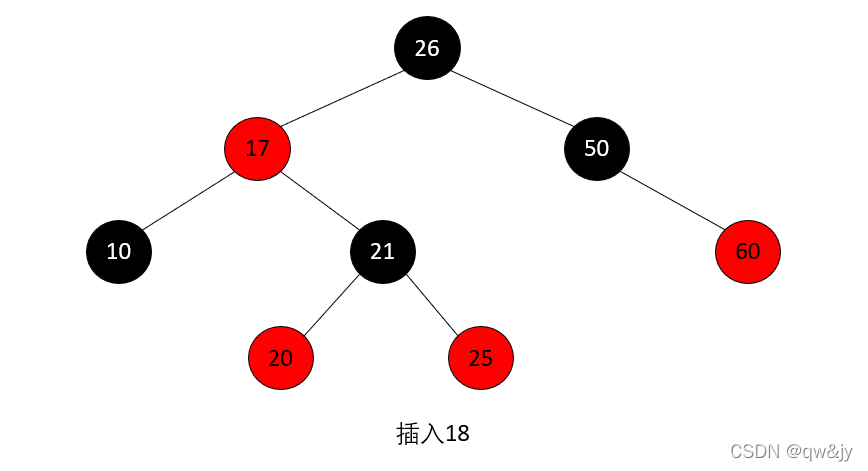

代码实现
插入代码:
void insert(BiTree z){//插入结点z,z的key属性已被事先赋值
BiTree y = NULL;
BiTree x = root;//root树根结点
while(x != NULL){//查找到z的插入位置
y = x;//y记录的是x的父结点
if(z->key < x->key)
x = x->left;
else
x = x->right;
}
z->parent = y;//z认y为父
if(y == NULL)//若y为NULL,则原树为空树
root = z;
else if(z->key < y->key)//z为y左孩子
y->left = z;
else//z为y右孩子
y->right = z;
z->left = NULL;//设置插入结点z的属性
z->right = NULL;
z->color = RED;//设置插入结点z为红色
insert_adjust(z);//调整红黑树
}
调整代码:
void insert_adjust(BiTree z){//调整红黑树的结构
while(z->parent->color == RED){//插入结点的父结点为红色
if(z->parent == z->parent->parent->left){//父亲是祖父的左孩子
BiTree y = z->parent->parent->right;//叔叔结点
if(y->color == RED){//叔叔为红结点:情况一
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else{
if(z == z->parent->right){//z结点为右孩子:情况二
z = z->parent;
Left_Rotate(z);
}
//z结点为左孩子:情况三
z->parent->color = BLACK;
z->parent->parent->color = RED;
Right_Rotate(z->parent->parent);
}
}
else{//父亲是祖父的右孩子
BiTree y = z->parent->parent->left;//叔叔结点
if(y->color == RED){//叔叔为红结点:情况一
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else{
if(z == z->parent->left){//z结点为右孩子:情况二
z = z->parent;
Right_Rotate(z);
}
//z结点为左孩子:情况三
z->parent->color = BLACK;
z->parent->parent->color = RED;
Left_Rotate(z->parent->parent);
}
}
}
root->color = BLACK;//最后将根节点置为黑色,以满足红黑规则,又不会破坏规则5
}
情况一:
z 的叔叔结点 y 是红色的(违反了性质四)
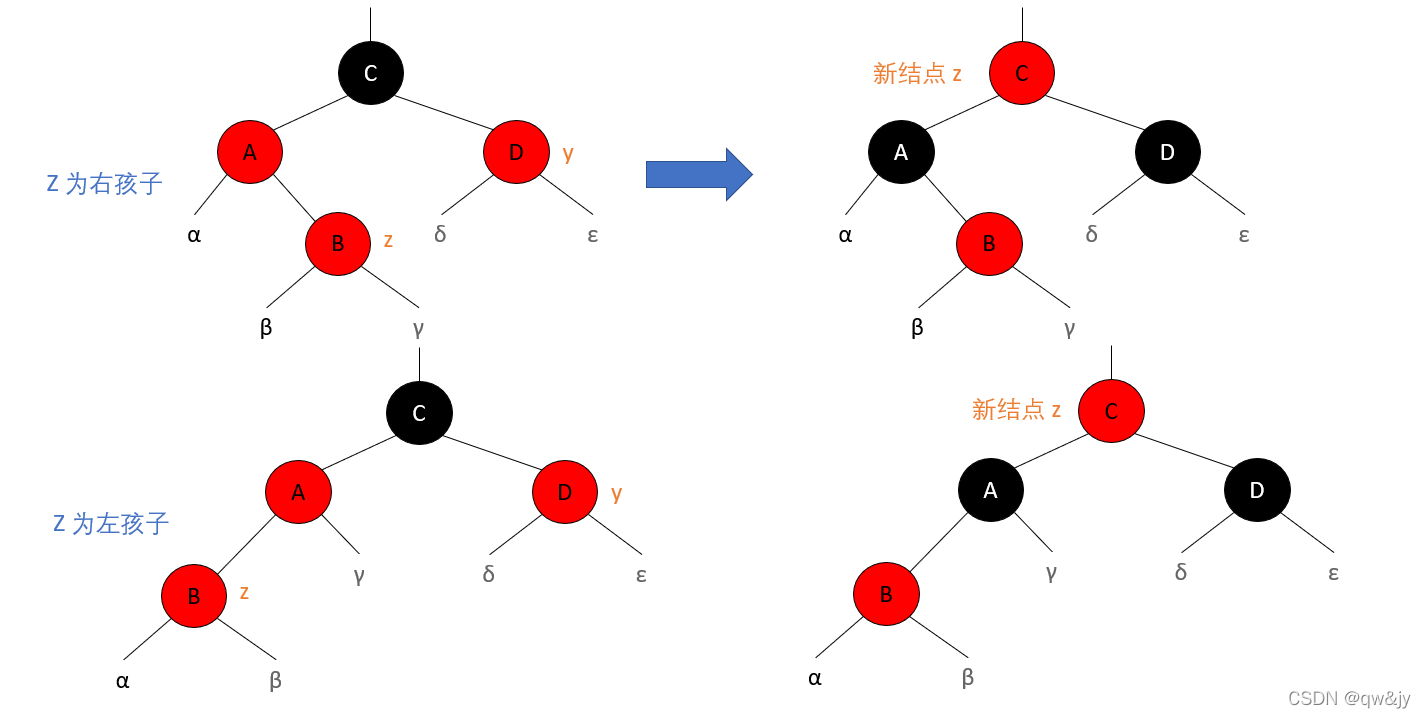
情况二:
z 的叔叔结点 y 是黑色的且 z 是一个右孩子
情况三:
z 的叔叔结点 y 是黑色的且 z 是一个左孩子
时间复杂度:O(lg n)
删除
红黑的删除分两步:① 二叉排序树的删除;② 结构调整。
删除情况(删除一个结点的颜色为它自身的颜色和替换它的结点颜色):
-
x 指向一个“红+黑”结点
将 x 设为一个“黑”结点。 -
x 指向根结点
将 x 设为一个“黑”结点。 -
x 指向一个“黑+黑”结点
[1] x 的兄弟结点是红的。
① 将 x 的兄弟结点设为“黑色”。
② 将 x 的父结点设为“红色”。
③ 对 x 的父结点进行左旋。
④ 左旋后,重新设置 x 的兄弟结点。
[2] x 的兄弟结点是黑色,x 的兄弟结点的两个孩子都是黑色。
① 将 x 的兄弟结点设为“红色”。
② 设置“x 的父结点”为“新的 x 结点”。
[3] x 的兄弟结点是黑色,x 的兄弟结点的左孩子是红色,右孩子是黑色的。
① 将 x 兄弟结点的左孩子设为“黑色”。
② 将 x 兄弟结点设为“红色”。
③ 对 x 的兄弟结点进行右旋。
④ 右旋后,重新设置 x 的兄弟结点。
[4] x 的兄弟结点是黑色,x 的兄弟结点的右孩子是红色,x 的兄弟结点的左孩子任意颜色。
① 将 x 父结点颜色,赋值给 x 的兄弟结点。
② 将 x 父结点设为“黑色”。
③ 将 x 兄弟结点的右子结点设为“黑色”。
④ 将 x 的父结点进行左旋。
代码
删除代码:
void transplant_RB(BiTree u,BiTree v){//v结点替换u结点
if(u->parent == NULL)//u是根结点
root = v;
else if(u == u->parent->left)//u是左孩子
u->parent->left = v;
else//u是右孩子
u->parent->right = v;
v->parent = u->parent;
}
void delete_RB(BiTree z){//删除结点z
y = z;
y_original_color = y->color;//记录y的颜色
if(z->left == NULL){//无左孩子
x = z->right;
transplant_RB(z, z->right);//用右子树顶替
}
else if(z->right == NULL){//无右孩子
x = z->left;
transplant_RB(z, z->left);//用左子树顶替
}
else{//左右孩子都有
y = TERR_MINISPLANT(z->right);//寻找z的中序后继结点
y_original_color = y->color;//记录y的颜色
x = y->right;//y的右孩子
if(y->parent == z)//y结点的父亲是z
x->parent = y;//
else{//y结点的父亲不是z
transplant_RB(y, y->right);//y的右孩子顶替y
y->right = z->right;//z的右孩子成为y的右孩子
y->right->parent = y;//z的右孩子让y为父亲
}
transplant_RB(z, y);//y顶替z
y->left = z->left;//y接手z的左孩子
y->left->parent = y;//z的左孩子认y为父
y->color = z->color;//y继承z的颜色
}
if(y_original_color == BLACK)//黑色需要调整
delete_adjust(x);//删除的调整,下面有详细代码
}
删除结点 z;若 z 的子结点少于 2 个时,z 从树中删除,并让 y 成为 z;若 z 有两个子结点时,y 应该是 z 的后继,并且 y 将移至树中的 z 位置。
在结点被移除或者在树中移动之前,必须记住 y 的颜色,并且记录结点 x 的踪迹,将 x 移至树中 y 的原来位置,因为结点 x 也可能引起红黑性质的破坏。
若结点 y 是黑色,则会产生三个问题,需要调整:
- 如果 y 是原来根结点,而 y 的一个红孩子成为新的根结点。(违反了性质 2)
- 如果 x 和 x 的父亲是红色的。(违反规则 4)
- 在树中移动 y 将导致先前包含 y 的任何简单路径上黑结点个数少 1。(y 的祖先违反性质 5)
删除调整:
void delete_adjust(BiTree x){//删除,调整红黑树
while(x != root && x->color == BLACK){//x不是根结点,且颜色为黑色
if(x == x->parent->left){//x是左孩子
BiTree w = x->parent->right;//兄弟结点
if(w->color == RED){//情况一:兄弟为红色
w->color = BLACK;//兄弟变为黑色
x->parent->color = RED;//父亲变为红色
Left_Rotate(x->parent);//父结点左旋
w = x->parent->right;//更新兄弟
}
if(w->left->color == BLACK && w->right->color == BLACK){//情况二:兄弟为黑色,左右侄子为黑色
w->color = RED;//兄弟变为红色
x = x->parent;//从父结点调整
}
else{
if(w->right->color == BLACK){//情况三:右侄子为黑色,左侄子为红色
w->left->color = BLACK;//左侄子变为黑色
w->color = RED;//兄弟变为红色
Right_Rotate(w);//兄弟右旋
w = x->parent->right;//更新兄弟
}
//情况四:左右侄子为红色
w->color = x->parent->color;//兄弟结点变为父结点的颜色
x->parent->color = BLACK;//父结点变为黑色
w->right->color = BLACK;//右侄子变为黑色
Left_Rotate(x->parent);//父结点左旋
x = root;//x指向根结点
}
}
else{
BiTree w = x->parent->left;//兄弟结点
if(w->color == RED){//情况一:兄弟为红色
w->color = BLACK;//兄弟变为黑色
x->parent->color = RED;//父结点变为红色
Right_Rotate(x->parent);//父结点右旋
w = x->parent->left;//更新兄弟,更新为右侄子
}
if(w->left->color == BLACK && w->right->color = BLACK){//情况二:兄弟为黑色,左右侄子为黑色
w->color = RED;//兄弟变为红色
x = x->parent;//从父结点调整
}
else{
if(w->left->color == BLACK){//情况三:左侄子为黑色,右侄子为红色
w->right->color = BLACK;//右侄子变为黑色
w->color = RED;//兄弟变为红色
Left_Rotate(w);//兄弟进行左旋
w = w->parent->left;//更新兄弟,更新为右侄子
}
//情况四:左右侄子为红色
w->color = x->parent->color;//兄弟变为父结点的颜色
w->left->color = BLACK;//父结点变为黑色
x->parent->color = BLACK;//父节点啊变为黑色
Right_Rotate(x->parent);//父结点右旋
x = root;//x指向根结点
}
}
}
x->color = BLACK;//x更新为黑色
}
情况一:
x 的兄弟结点 w 是红色的
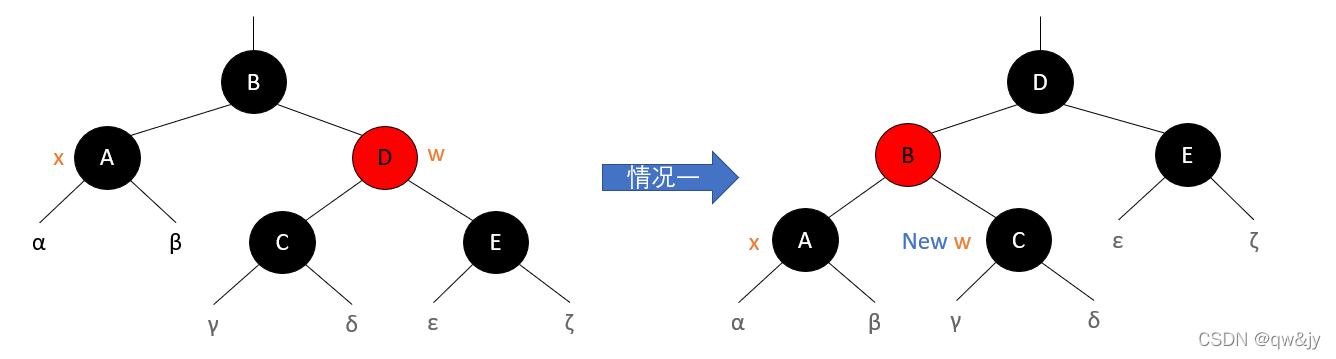
情况二:
x 的兄弟结点 w 是黑色的,而且 w 的两个子结点都是黑色的
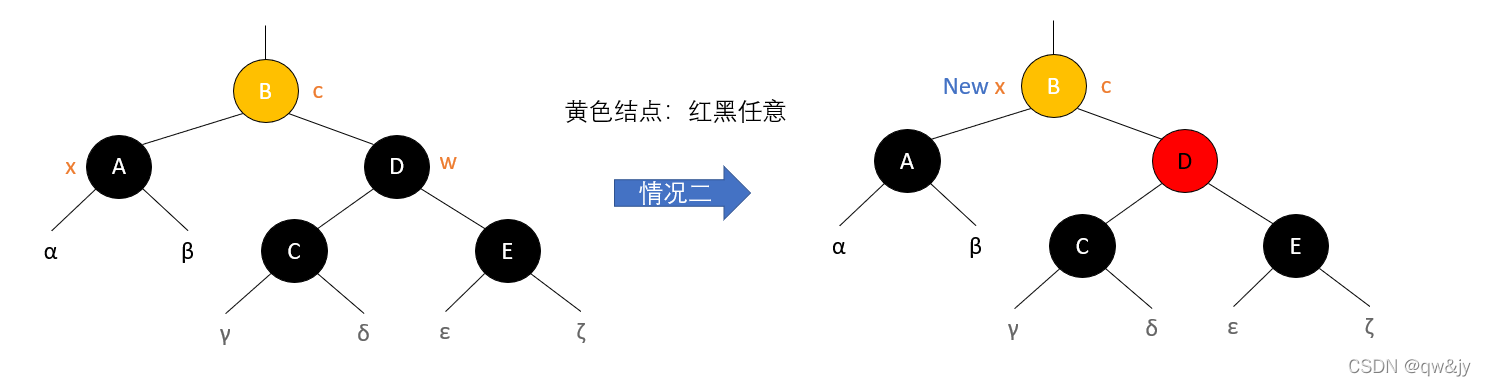
情况三:
x 的兄弟结点 w 是黑色的,而且 w 的右孩子是红色的,w 的右孩子是黑色的
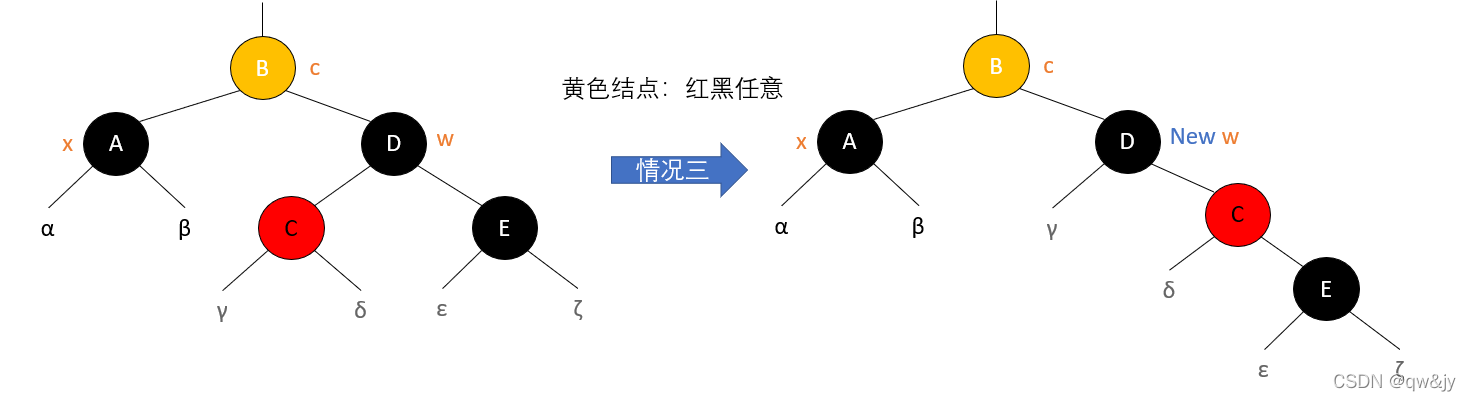
情况四:
x 的兄弟结点 w 是黑色的,且 w 的右孩子是红色的
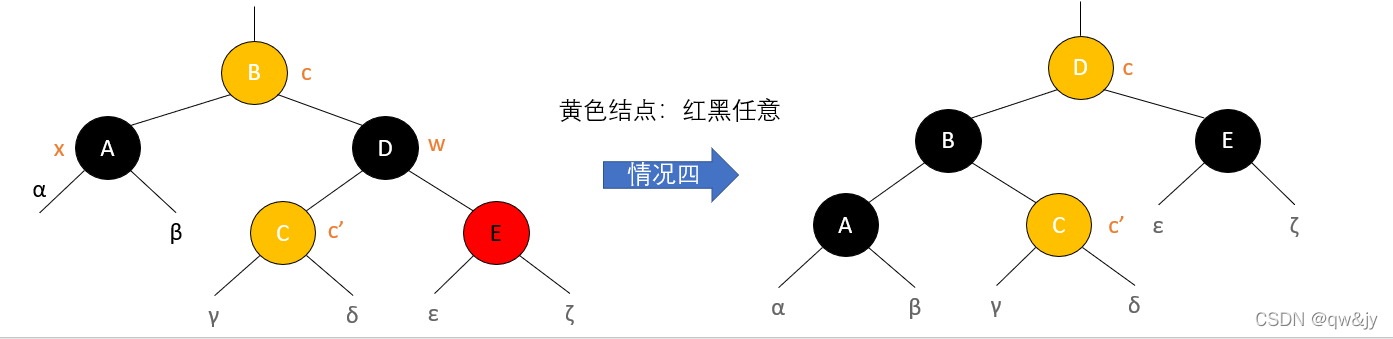
时间复杂度:
O(lg n)
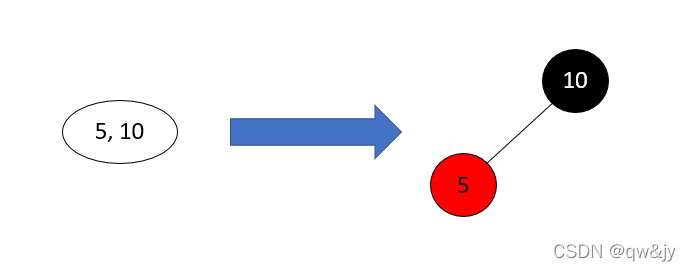
2-3树转红黑树
2-结点

3-结点
2-3-4树转红黑树
2-结点

3-结点
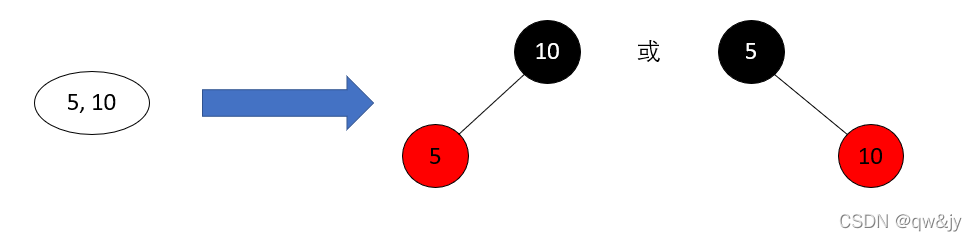
4-结点