目录

435. 无重叠区间移除元素的最小个数

无重叠区间 区间组合结果

合并区间_牛客题霸_牛客网

435. 无重叠区间

移除元素的最小个数

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

来源：力扣（LeetCode）

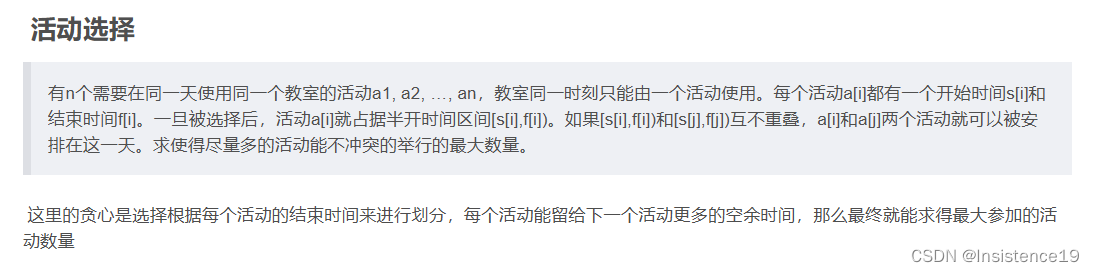
与上一博文活动安排那个题比较类似，那个是求活动的最大数量，那么就可以求出一个时间不冲突的区间的最大数量，用数组长度减去这个最大数量不就是我需要移除的元素最小数量嘛，就在返回结果上和之前不一样即可。

【解法一】将结束时间进行排序

class Com
{
    public:
        bool operator()(const vector<int>& left, const vector<int>& right)
        {
            return left[1]<right[1];
        }
};

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), Com());
        int pos = 0;
        int num = 1;
        for(int i = 1; i < intervals.size(); i++)
        {
            if(intervals[i][0] >= intervals[pos][1])
            {
                pos = i;
                num++;
            }
        }
        return intervals.size()-num;
    }
};

【解法二】将开始时间进行排序

如果是上述情况，不发生重叠，那么只需要更新pos位置即可，不需要移除元素

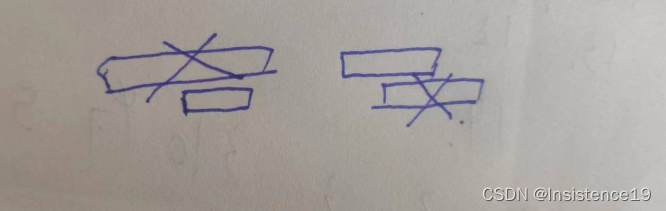
如果发生重叠，根据贪心思想，我需要给后面区间尽可能多的留出空间

所以遇到下一区间是前一个区间的子区间情况，移除前一个，保留下一个，更新pos位置

如果后一个区间end大于前一个区间的end那么移除后一个区间，不进行更新pos

class Com
{
    public:
        bool operator()(const vector<int>& left, const vector<int>& right)
        {
            return left[0]<right[0];
        }
};

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), Com());
        int pos = 0;
        int num = 0;
        for(int i = 1; i < intervals.size(); i++)
        {
            // 俩个活动不影响
            if(intervals[pos][1] <= intervals[i][0])
            {
                pos = i;
            }
            else
            {
                // 如果发生重叠，根据贪心思想，我需要给后面区间尽可能多的留出空间
                // 所以遇到下一区间是前一个区间的子区间情况，移除前一个，保留下一个更新pos位置
                // 如果后一个区间end大于前一个区间的end那么移除后一个区间，不进行更新pos
                if(intervals[pos][1] > intervals[i][1])
                    pos = i; 
                num++;
            }
        }
        return num;
    }
};

无重叠区间 区间组合结果

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠

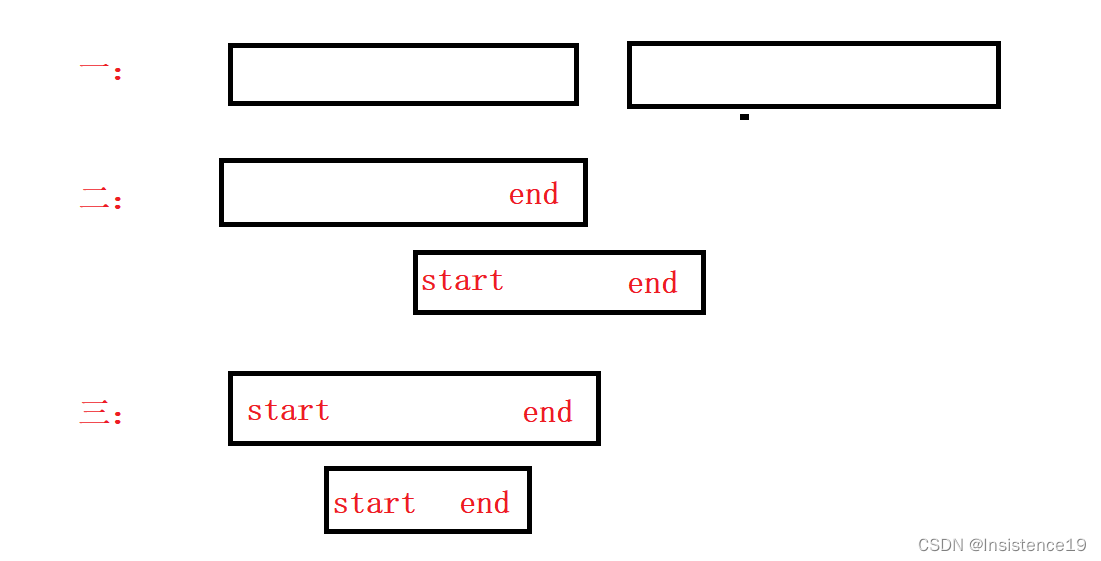
分成这三种情况哈，直接对应其各种类型进行处理即可（注意：划分不重复区间）

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Com
{
public:
    // 按start先后进行排序
    bool operator()(const Interval& left, const Interval& right)
    {
        return left.start < right.start;
    }
};

class Solution {
public:
    vector<Interval> merge(vector<Interval> &intervals) 
    {
        sort(intervals.begin(), intervals.end(), Com());
        for(int i = 0; i < intervals.size()-1;)
        {
            if(intervals[i].end <= intervals[i+1].start)
                i++;
            else if(intervals[i].end > intervals[i+1].start && intervals[i].end < intervals[i+1].end)
                intervals.erase(intervals.begin()+i+1);
            else if(intervals[i].end >= intervals[i+1].end)
                intervals.erase(intervals.begin()+i);
        }
        return intervals;
    }
};

合并区间_牛客题霸_牛客网

给出一组区间，请合并所有重叠的区间。

请保证合并后的区间按区间起点升序排列。

数据范围：区间组数 0≤n≤2×1050≤n≤2×105，区间内 的值都满足 0≤val≤2×1050≤val≤2×105

要求：空间复杂度 O(n)O(n)，时间复杂度 O(nlogn)O(nlogn)

进阶：空间复杂度 O(val)O(val)，时间复杂度O(val)O(val)

【解法一】重复的就进行合并，不重复的保留

空间复杂度O(1) 就是超时了。

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Com
{
public:
    bool operator()(const Interval& left, const Interval& right)
    {
        return left.start < right.start;
    }
};

class Solution {
public:
    vector<Interval> merge(vector<Interval> &intervals) 
    {
        if(intervals.size()==0)return intervals;
        sort(intervals.begin(), intervals.end(), Com());
        for(int i = 0; i < intervals.size()-1;)
        {
            if(intervals[i].end < intervals[i+1].start)
                i++;
            else if(intervals[i].end >= intervals[i+1].start && intervals[i].end < intervals[i+1].end)
            {
                intervals[i].end = intervals[i+1].end;    // 进行更新第一个区间的end
                intervals.erase(intervals.begin()+i+1); // 删除第二个子区间
            }  
            else if(intervals[i].end >= intervals[i+1].end)
                intervals.erase(intervals.begin()+i+1); // 删除这个子区间
        }
        return intervals;
    }
};

【解法二】空间换时间  用一个res容器来进行接受结果

对几种情况分好类就行

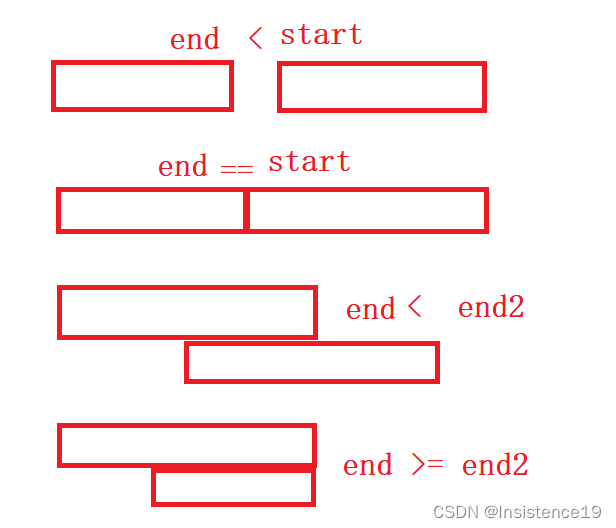
if(res.back().end < intervals[i].start)

res.push_back(intervals[i]);

else if(res.back().end == intervals[i].start)

res.back().end = intervals[i].end;

else if(res.back().end < intervals[i].end)

res.back().end = intervals[i].end;

else if(res.back().end >= intervals[i].end)

continue;

算法时间进行改进

上方代码加粗部分可以进行同样的操作，可以看出下面三种情况都满足end1 >= start2，前俩种选择end2进行更新back()、而最后一种选择end1进行更新，都选择的是最大的end所以使用

end = max(end1, end2)；

只有在俩个区间完全没有重叠的情况下，才会执行push_back操作

if(intervals[i].start <= res.back().end)


res.back().end = max(res.back().end, intervals[i].end);


else

res.push_back(intervals[i]);

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 *     Interval() : start(0), end(0) {}
 *     Interval(int s, int e) : start(s), end(e) {}
 * };
 */
class Com
{
public:
    bool operator()(const Interval& left, const Interval& right)
    {
        return left.start < right.start;
    }
};

class Solution {
public:
    vector<Interval> merge(vector<Interval> &intervals) {
        vector<Interval> res;
        if(intervals.size()==0)return res;
        sort(intervals.begin(), intervals.end(), Com());
        res.push_back(intervals[0]);
        for(int i = 1; i < intervals.size(); i++)
        {
            if(intervals[i].start <= res.back().end)
                res.back().end = max(res.back().end, intervals[i].end);
            else                 
                res.push_back(intervals[i]);
        }
        return res;
    }
};