博客

在以往的动态平衡数据结构中，我们学习过AVL tree, RB tree等等。二者的对元素的插入，删除，访问的时间复杂度都为对数时间。但是二者相对比较复杂，构建也比较麻烦（尤其是RB树，太难了~~）。有没有也存在一种动态平衡的数据结构，对元素的插入，删除和访问操作为对数时间尼？当然有！ 那就是跳跃表。

我们都知道链表的插入或者删除操作的时间复杂度为常数时间，但是其索引元素的时间复杂度便为线性时间。有什么什么办法可以提高其搜索的时间效率尼？

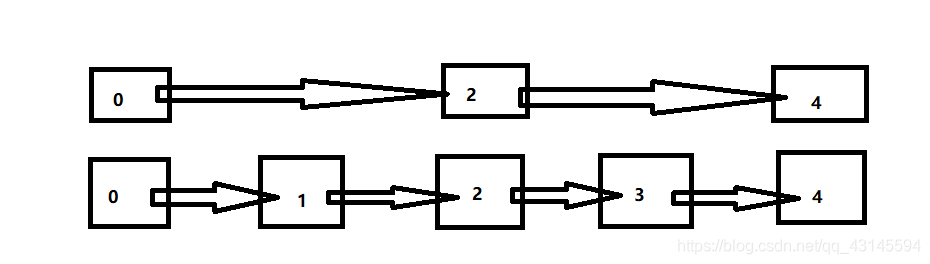
我们可以通过增加层数，提高搜索元素的效率。比如下图：当只存在单层链表时，如果我们要搜索元素4，我们必须对链表进行一层遍历至链表末尾才可以找到元素。当我们增加层数时（我们假设第一层与第二层的节点个数比值为1：2），我们只需要遍历一半的链表节点数，便可以找到该元素，如果继续增加层数时，我们遍历的链表节点数会更少。此时，通过对链表进行加层而构成的的数据结构，我们称为跳跃表。

链表中会有元素的插入操作，跳跃表也不例外。那该怎么插入尼？难道要一直把元素插入到第一层吗？ 这样随着插入数据的增多，跳跃表会逐渐演化成单链表。那该怎么办尼？ 我们可以随机的觉得其插入的层数，通过抛硬币来解决，如果正面朝上，增加层数（每次加一），直到出现反面为止。这样既可以保证不会出现形成单链表的情况，而且还满足其插入操作的时间复杂度为对数时间。

跳跃表的节点：

struct Node {
	int   value = -1;  //默认节点的value为1
	int   level;      // 节点的层数
	Node** next;     // 存放指向下一节点的指针
public:
	Node(int _value, int _level) :value(_value), level(_level), next(new Node*[_level]()) {};
	~Node() { if (next != nullptr) { delete[] next; } };
};

插入操作：

void SkipList::Insert(const int value) {
	auto level = getlevel();
	Node* newnode = new Node(value, level);
	Node** update = new Node*[level](); //存放要插入的位置的前驱的节点的地址

	Node* temp = head;
	for (int i = level - 1; i >= 0; --i) {  //一般从上向下进行搜索
		while (temp->next[i] != nullptr && temp->next[i]->value < value) {
			temp = temp->next[i];        //满足条件向下移动
		}
		update[i] = temp;
	}

	for (int i = 0; i < level; ++i) {     //先将newnode与前驱节点的下一节点进行连接，然后将前驱节点与newnode进行相连，其实与链表的插入是一样的
		newnode->next[i] = update[i]->next[i];
		update[i]->next[i] = newnode;
	}

	if (level > levelcount) {  //对层数进行更新
		levelcount = level;
	}
	++size;
	std::cout << value << "success" << std::endl;
}

随机的构造层数：

int SkipList::getlevel()const {
	int level = 1;
	std::random_device rd;
	std::mt19937 gen(rd());
	std::uniform_int_distribution<>dis(1, 1000);
	while (true) {
		auto nums = dis(gen);
		if (nums % 2 == 0) {
			++level;
		}
		else {
			break;
		}
	}
	std::cout << "level: " << level << std::endl;
	return level;
}

跳跃表的删除：

void SkipList::Delete(const int value) {
	Node** update = new Node * [levelcount];
	Node* temp = head;

	for (int i = levelcount - 1; i >= 0; --i) {
		while (temp->next[i] != nullptr && temp->next[i]->value < value) {
			temp = temp->next[i];
		}
		update[i] = temp;
	}

	if (temp->next[0] != nullptr && temp->next[0]->value == value) {
		--size;
		std::cout << value << "delete" << std::endl;
		for (int i = levelcount - 1; i >= 0; --i) {
			if (update[i]->next[i] != nullptr && update[i]->next[i]->value == value) {
				update[i]->next[i] = update[i]->next[i]->next[i];  //与链表的删除操作一样
			}
		}
	}
}

跳跃表的访问元素的操作（

跳跃表的索引操作可以抽象成一颗树，然后进行二分搜索

）：

Node* SkipList::Find(const int value)const {
	Node* temp = head;
	for (int i = levelcount - 1; i >= 0; --i) {
		while (temp->next[i] != nullptr && temp->next[i]->value < value) {
			temp = temp->next[i];
		}
	}

	if (temp->next[0] != nullptr && temp->next[0]->value == value) {
		std::cout << value << " success" << std::endl;
		return temp->next[0];
	}
	else {
		return nullptr;
	}
}

完整代码如下：

#include<iostream>
#include<random>
struct Node {
	int   value = -1;
	int   level;
	Node** next;
public:
	Node(int _value, int _level) :value(_value), level(_level), next(new Node*[_level]()) {};
	~Node() { if (next != nullptr) { delete[] next; } };
};

class SkipList {
public:
	SkipList(const int _maxlevel) :maxlevel(_maxlevel), head(new Node(-1, _maxlevel)), size(0), levelcount(1) {};
	~SkipList() {
		if (head != nullptr) {
			delete head;
		}
	}
public:
	Node* Find(const int value)const;
	void  Insert(const int value);
	void  Delete(const int value);
	void  Display()const;
private:
	int    maxlevel; //最大层数
	Node*  head;     
	int    size;  //跳跃表中节点个数
	int    levelcount;  //跳跃表中当前的层数
private:
	int   getlevel()const;
};

Node* SkipList::Find(const int value)const {
	Node* temp = head;
	for (int i = levelcount - 1; i >= 0; --i) {
		while (temp->next[i] != nullptr && temp->next[i]->value < value) {
			temp = temp->next[i];
		}
	}

	if (temp->next[0] != nullptr && temp->next[0]->value == value) {
		std::cout << value << " success" << std::endl;
		return temp->next[0];
	}
	else {
		return nullptr;
	}
}

void SkipList::Insert(const int value) {
	auto level = getlevel();
	Node* newnode = new Node(value, level);
	Node** update = new Node*[level]();

	Node* temp = head;
	for (int i = level - 1; i >= 0; --i) {
		while (temp->next[i] != nullptr && temp->next[i]->value < value) {
			temp = temp->next[i];
		}
		update[i] = temp;
	}

	for (int i = 0; i < level; ++i) {
		newnode->next[i] = update[i]->next[i];
		update[i]->next[i] = newnode;
	}

	if (level > levelcount) {
		levelcount = level;
	}
	++size;
	std::cout << value << "success" << std::endl;
}

void SkipList::Delete(const int value) {
	Node** update = new Node * [levelcount];
	Node* temp = head;

	for (int i = levelcount - 1; i >= 0; --i) {
		while (temp->next[i] != nullptr && temp->next[i]->value < value) {
			temp = temp->next[i];
		}
		update[i] = temp;
	}

	if (temp->next[0] != nullptr && temp->next[0]->value == value) {
		--size;
		std::cout << value << "delete" << std::endl;
		for (int i = levelcount - 1; i >= 0; --i) {
			if (update[i]->next[i] != nullptr && update[i]->next[i]->value == value) {
				update[i]->next[i] = update[i]->next[i]->next[i];
			}
		}
	}
}

void SkipList::Display()const {

	Node* temp = head;
	while (temp->next[0] != nullptr) {
		std::cout << temp->next[0]->value << "  " << std::endl;
		temp = temp->next[0];
	}
}


int SkipList::getlevel()const {
	int level = 1;
	std::random_device rd;
	std::mt19937 gen(rd());
	std::uniform_int_distribution<>dis(1, 1000);
	while (true) {
		auto nums = dis(gen);
		if (nums % 2 == 0) {
			++level;
		}
		else {
			break;
		}
	}
	std::cout << "level: " << level << std::endl;
	return level;
}

int main(void) {

	SkipList list(12);
	for (int i = 1; i < 20; ++i) {
		list.Insert(i);
	}
	list.Display();
	list.Delete(4);
	std::cout << std::endl;
	
	list.Display();

	std::cout << list.Find(2)->value << std::endl;


	return 0;
}

参考：

https://blog.csdn.net/m0_37907797/article/details/102661778