博客

目录

跳表的数据结构和复杂度

跳表的索引

ConcurrentSkipListMap数据结构

前面分析过二分查找的时间复杂度是O(logN)，但是只能作用于数组的数据结构之上，并且有序。那么基于链表是否可以实现添加、删除、查询的时间复杂度都是O(logN)呢？跳表。跳表的思想就是链表每【几个】数据节点就往上抽取一层索引，如果索引链表本身比较长那么可以在一级索引的基础上隔几个索引节点就往上抽取一层索引。

跳表的数据结构和复杂度

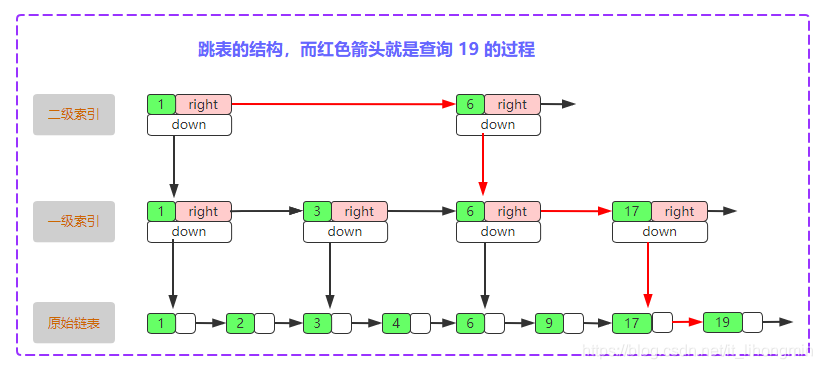
跳表的数据结构如上图，索引中有两个指针，向右指针指向本级索引的下一个节点，向下指针指向【上】一级索引的节点，跳表中索引层级从小到大依次是向上。如果在原始链表中查询一个值的话时间复杂度是O(N)，途中红色箭头是跳表的查询路径，整个查询的路径与索引总层数和每多少个元素往上抽取一层有关。就拿每两个节点往上抽取一层看，如果想查询节点为4的元素，一级索引层只需要查询3个节点，因为节点查询到3时，一定满足 3 > 1 && 3 < 6 的（3和6是上一层索引的节点），即非顶级索引层查询的节点数是固定的常数（那么就与时间复杂度无关）。

每两个节点往上抽取一个索引,那么一级二级一直到


k


级所有的节点数就是： n/2，n/4，n/8，*** n/2^k ，由于每层需要遍历的节点数是固定的3，那么


跳表查询的时间复杂度为 O(logN)


。从链表可知新增删除的本身复杂度是O(1)，新增或者按照值删除的时间复杂度依赖查询的时间复杂度，


跳表


依赖索引查询所以


删除和新增的时间复杂度也是O(logN)


。

由上面可知索引节点的个数为 n/2 + n/4 + n/8 + *** + 4 + 2 + 1 = n – 2；每三个节点抽一个索引时，索引节点数量为 n/3 + n/9 + n/27 + *** + 9 + 3 + 1 = n/2；所以空间复杂度与平均每多少个节点抽取一个有关，用大O时间复杂度表示跳表的


空间复杂度都是O(n)


，但是其实真正使用时远小于N。 再加上，其实我们使用跳表时，存储数据的对象本身可能远大于索引的两个指针，比如我们存储一个链表的对象使用了 1K，但是索引的指针本身单位为字节，完全可以忽略不计。

跳表的索引

跳表的索引真正创建是在添加元素的时候，一般根据随机函数生产。即如果是三个节点抽取一个索引，那么我们就让随机函数返回创建一级所以的概率为 1/3,二级索引概率为 1/9 … 即可。比如：

public class SkipList {
    // 往上抽取的概率，0.5就是两个值抽取一个
    private static final float SKIPLIST_P = 0.5f;
    // 最大的索引层级
    private static final int MAX_LEVEL = 16;

    /**
     * 理论来讲，一级索引中元素个数应该占原始数据的 50%，二级索引中元素个数占 25%，三级索引12.5% 
     * ，一直到最顶层。因为这里每一层的晋升概率是 50%。对于每一个新插入的节点，都需要调用
     *  randomLevel 生成一个合理的层数。该randomLevel方法会随机生成 1~MAX_LEVEL 之间的数，且 ：
     *   50%的概率返回 1
     *   25%的概率返回 2
     *   12.5%的概率返回 3 ...
     * @return
     */
    private int randomLevel() {
        int level = 1;
        while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {
            level += 1;
        }
        return level;
    }
}
    

Java中只有ConcurrentSkipListMap使用了跳表的数据结构，看看其随机函数的实现相对复杂，但是思路也是基于随机概率进行处理，也是发生在put(key, value)操作时：

private V doPut(K key, V value, boolean onlyIfAbsent) {
    // 先省略一万行。。。
    // 由于ConcurrentSkiplistMap本身需要支持并发，所以基于线程安全实现的随机数
    int rnd = ThreadLocalRandom.nextSecondarySeed();
    // 再执行位运算，总之就是随机数的思想
    if ((rnd & 0x80000001) == 0)  // test highest and lowest bits

    // 再省略一万行
    return null;
}

ConcurrentSkipListMap数据结构

这里只站在数据结构的角度分析ConcurrentSkipListMap，并发等不考虑。

Java的集合中有基于散列表实现的非线程安全的HashMap，也有基于AQA实现的线程安全的ConcurrentHashMap；有基于红黑树实现的 TreeMap主要用于按照key排序，可以自然排序也可以基于我们实现的Comparator接口规则进行排序，只是TreeMap本身是非线程安全的。我们可以使用Collections.synchronizedMap(new HashMap()) 实现一个线程安全的散列表容器，也可以基于Collections.synchronizedSortedMap(new TreeMap<>())实现一个线程安全的TreeMap，当然本质比较简单就是所有方法都添加synchronized关键字。按道理，散列表的数据结构有 非线程安全的HashMap对应线程安全的ConcurrentHashMap，那么应该有一个基于红黑树实现的 非线程安全的TreeMap对应线程安全的ConcurrentTreeMap，结果没有，但是有一个基于跳表实现的 ConcurrentSkipListMap。

个人猜想，Doug Lea此处使用了跳表数据结构去实现了“本应该”使用红黑树的实现的 可以根据Key排序的K-V集合。其实像跳表一样可以支持快速的查询、新增、删除的数据结构还有红黑树、B+树等。只是红黑树诞生是在1972年，而跳表的出现是1989年，但是跳表确实是一个比红黑树容易实现，并且性能比较优秀的数据结构。个人总结了一下三种数据结构的对比（所以基于跳表替换红黑树完全可行，其实只要对跳表再稍加改造也可以替代B+树，只是出现的历史早晚原因等，，，个人猜想而已）：

ConcurrentSkipListMap的结构包括数据结构和索引结构，而索引结构本身包含了单链表的数据结构如下：

static final class Node<K,V> {
    // key，value比较好理解
    final K key;
    volatile Object value;
    // Node类型的单链表指针 
    volatile Node<K,V> next;
}

static class Index<K,V> {
    // 数据节点的信息
    final Node<K,V> node;
    // Index类型的指针，指向同级索引的下一个节点
    final Index<K,V> down;
    // Index类型的指针，指向上一级（跳表索引第一层在最下面）索引的节点
    volatile Index<K,V> right;
}

而ConcurrentSkipList中只存储了顶级索引的第一个节点，该节点数据结构如下（增加了level属性，用于说明当前的索引层级高度），即ConcurrentSkipListMap只有一个HeadIndex head属性，就可以查询到整个跳表：

/**
 * The topmost head index of the skiplist.
 */
private transient volatile HeadIndex<K,V> head;

static final class HeadIndex<K,V> extends Index<K,V> {
    final int level;

    HeadIndex(Node<K,V> node, Index<K,V> down, Index<K,V> right, int level) {
        super(node, down, right);
        this.level = level;
    }
}

Doug Lea的 Index类注释说明了，虽然索引中包含了节点的引用（指针）那么就可以拿到节点的信息，但是他们使用的指针方式完全不同，索引使用的指针是Index类型的down和right，而数据节点的单链表使用的是Node类型的next指针。如下图：