摘要
在本文中,我们提出了一种基于残差的双域优化网络(DRONE)。 DRONE 由三个模块组成,分别用于嵌入、细化和感知。在嵌入模块中,首先扩展了一个稀疏的正弦图。然后,图像域网络有效地抑制了稀疏视图伪影。之后,细化模块侧重于协同恢复残差数据和图像域中的图像细节。最后,对数据和图像域中嵌入和细化组件的结果进行正则化,以优化感知模块中的图像质量,从而通过压缩感知的内核感知确保测量值(应该是指得到的投影数据)和图像之间的一致性。
介绍
目前的研究进展:常用的稀疏视图CT图像质量与100多个视图相关联,本文提出的方法将100压缩到60,且图像质量无显著退化。作者表示,受迭代思想的启发,有许多基于深度模型的迭代算法被提出,但是由于其巨大的计算开销,很难在实践中实现。此外,学习到的网络通常在图像上工作,性能可能会像传统的迭代算法一样受到迭代的影响。因此,这些现有的网络架构在超稀疏视图(<100 个视图,例如 60 个视图)的情况下无法提供良好的重建质量。
为了重建稀疏视图 CT 的准确图像,作者提出了一种基于残差的双域优化网络 (DRONE)。它由三个关键模块组成,分别是
嵌入、细化和感知
,以系统地减少测量误差并在分析和数据驱动的先验辅助下基于稀疏视图测量提高重建质量。
在嵌入模块中,首先使用数据扩展子网络来修复稀疏的测量数据并形成高维数据集。
扩展数据可能会引入错误
。然后,图像域处理子网络对使用分析方法(例如,滤波反投影(FBP)或反投影滤波(BPF))重建的初始图像进行后处理,以消除子采样伪影。
在细化模块中,结合了两个残差网络(一个用于数据残差,另一个用于图像残差)以细化结构细节。细化模块不仅减少了子采样伪影,而且提高了图像精度。需要强调的是,虽然基于深度学习的重建方法往往具有出色的重建性能,但由于缺乏所谓的“内核意识”,其鲁棒性、稳定性和泛化性问题仍然是实际应用的障碍。
另一方面,压缩感知(CS)方法具有这种意识,在图像重建中表现出良好的稳定性和泛化性。因此,我们最终在感知模块中引入了一种感知机制,以使用 CS 模型规范数据和图像域中嵌入和细化模块的深度先验。这种感知功能克服了实际测量和学习估计之间的差异,以在准确性和鲁棒性方面优化重建性能。
主要创新点: 在嵌入模块中使用编码解码网络来提取数据和图像域中的深层特征。此外,还集成了具有 Wasserstein 距离 (WGAN) 的生成对抗网络,以保留图像域中的细节和特征。其次,将数据残差和图像残差网络结合在细化模块中,以从嵌入模块的输出中恢复细微的结构特征。第三,根据 CS 迭代重建模型对数据和图像域中的深度先验进行正则化,以确保DRONE 网络的鲁棒性。
方法
1. CT Imaging Model
这部分为CT重建领域常谈之题:重建过程建模,有所了解者3可以跳过前两个公式。
(公式1)
上式
,其中J1表示投影视图数量,J2表示接收器数量,A是CT系统矩阵。
是投影噪声。由于稀疏视图重建问题的不适定性,很难直接使用矩阵求逆技术求解公式(1)。因此通过最小化优化函数来迭代求解,例如:
(公式2)
例如,公式(2) 可以使用 ART 或 SART 方法最小化。为了获得更好的解决方案,可以加入一个表示先验知识的正则化项,我们有 :
(公式3)
上面这个式子有两个术语:数据保真项
和正则化项
。在这种情况下,正则化先验的各种选择对应于不同的重建方法;例如,稀疏性、低秩、字典学习等。
2. DRONE Architecture
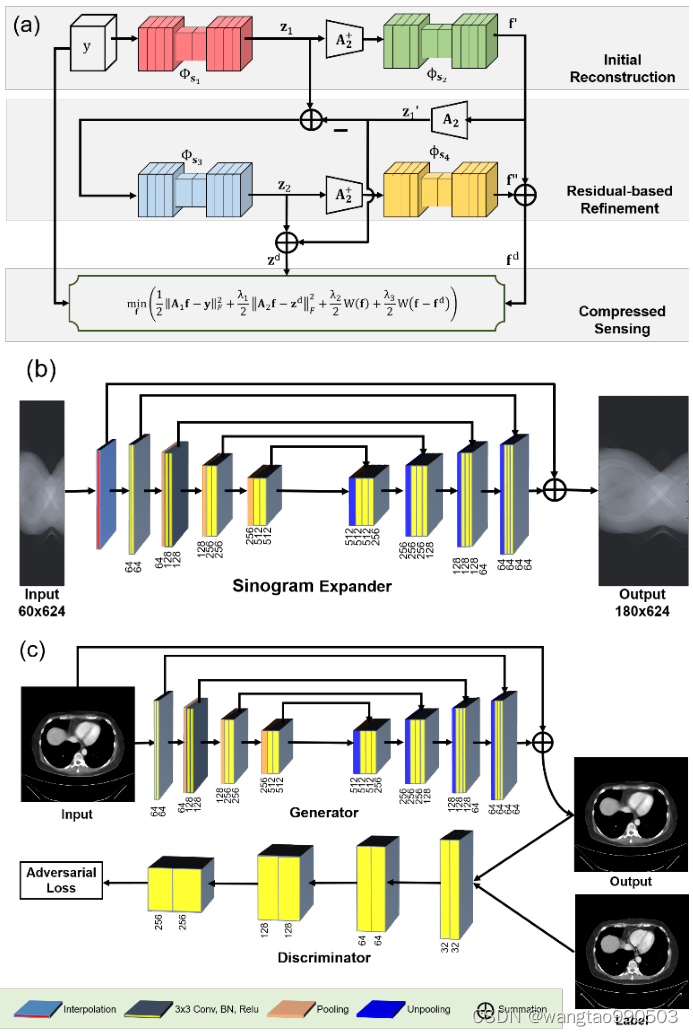
图 1 展示了 DRONE 的流程图。嵌入、细化和感知分别包含三个关键组件(图 1(a))。嵌入和细化模块都包含两个子网络,其中一个用于投影估计,另一个用于图像重建。
(1) Embedding Module
该模块有俩功能,第一个是将稀疏视图数据扩展到更高维,实际上就是把只有60个视图的数据扩展到180视图(为什么不扩展到360?因为180已经足够生成完整的图像,且扩展的视图距离原始数据太远的话失真严重)。这一过程通过投影网络
实现,S1表示网络参数。
第二个是图像域后处理,将上述扩展后的数据经过FBP后得到的图像进行处理,得到改进图像
,由图像域网络
实现,最终公式如下:
(公式4)
其中 A 表示 FBP 重建采用 180 个视图。
第一个网络是标准的UNet型的编码解码网络(图1(b)),网络使用MSE损失,在训练过程中,先通过最近邻插值对原始数据进行扩展,然后通过网络对简单插值后的数据进行细化,但受限于在原始数据的位置将原始输入保留为输出(意思就是细化后再把原始数据对应的视图数据覆盖回去),以确保一致性。
而第二个网络是从图像到图像的优化,不能使用MSE损失,因为它会导致边缘过度平滑和细节方面的丢失,作者选择的WGAN网络的Wasserstein 距离作为损失来训练网络。在 WGAN 训练中,通过最小化以下目标函数来优化 D 和 G:
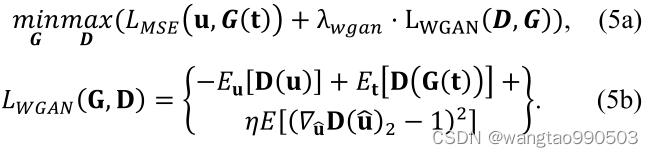
(2) Refinement Module
细化模块也由两部分组成:数据残差网络和图像残差网络。嵌入模块的输出
和对应的真实标签
是有差距的。来自
的重采样残差数据可以表示为
。作者训练了第三个网络
来处理残差数据,使用MSE损失。因此,细化模块的估计数据残差
表示为:
(公式6)
正弦数据有差异,图像数据也有差异,于是作者给出了第四个网络
图像残差网络,损失函数为MSE。于是有公式:
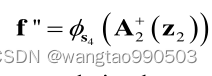
值得一提的是,数据残差网络比图像残差网络更容易训练,所以只需要少量的数据。由以上网络结果,我们可以同时改进高维数据和对应的图像。
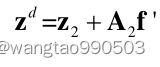
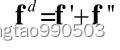
上式为:嵌入模块生成图像
经过投影变换后加上数据残差得到输出正弦数据;生成图像
加上图像残差得到输出图像。
(3) Awareness Module
对于稀疏视图CT,CS(压缩感知)展现了很有前景的实用性,例如,总变化最小化(TV)方法有利于边缘保留的图像恢复。在这里,我们使用一个名为总差(total difference)的变体,f 的总差可以定义为:

其中沿图像边界的梯度幅度设置为零。
初始化和约束对于从二次采样测量重建图像起着重要作用,因为它们可以缩小解空间中的可行区域。这个想法导致我们将支持深度学习的数据图像先验
与 CS 框架结合为:

其中
用来平衡两个数据保真项
和
,
表示投影到低维数据域的系统矩阵。如果 dz 的误差很小,我们应该为
选择一个较大的值。
和
是正则化的超参数,用于平衡数据保真度项和正则化先验。
上式考虑来自神经网络的数据图像先验,因为需要 L1 范数优化。由于很难直接获得解,我们引入两个向量 v1 和 v2 分别替换 W f 和 W
。此时上式变形为以下有约束优化问题:
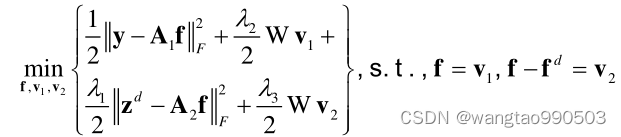
在适当条件下可以转化为如下无约束优化问题:
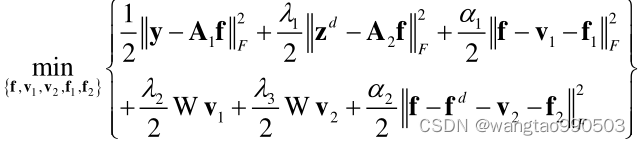
其中
和
是误差向量,
和
是耦合系数。注意到上式中有五个变量,可分为以下五个子问题:
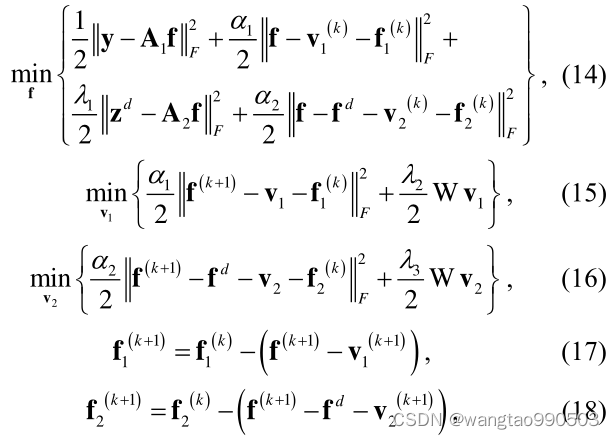
其中 k 表示当前迭代的索引。关于子问题14,最小化器满足导数等于零的条件,即:
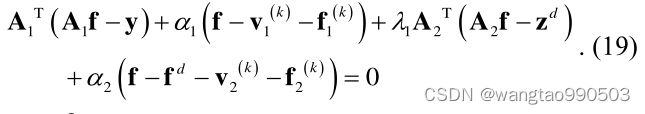
最后,
可以被更新为:
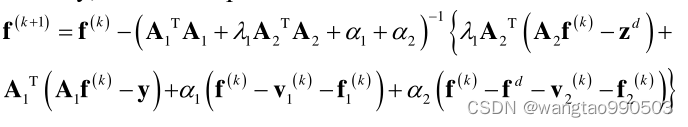
其中
和
可以使用 ART、SART 或其他经典算法计算。如前所述,解析重构方法,即
和
可以替换为
和
,并且
和
可以被视为相同变换。这里 FBP 用于快速初始图像重建。方程(15)的优化是总变异(TV)最小化问题。
我们首先将
和
替换为
和
,然后将方程10带入方程15得到:
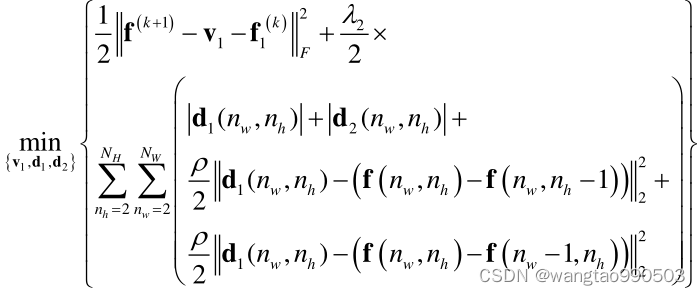
其中 v1 使用 Chambolle Antonin 方法更新。方程 (21) 是使用 TV 最小化的典型图像恢复任务,使用交替最小化策略更新三个变量(即
、
和 v1)。
实验与结果
老规矩,在这里就不写了,感兴趣的读者可以下载原文。