脉冲压缩(匹配滤波)
原因:
又要能量大(脉冲宽),又要分辨率高(脉冲窄),所以发宽脉冲,再把宽的回波脉冲压缩一下(在时域)。
在探测过程中,接收信号必须具有足够强的能量和足够好的分辨率。如果发射脉冲的持续时间(脉冲宽度)为T,则每一目标在回波数据中占据相同的时间间隔T,故压缩前的可分辨能力为
ρ
=
T
\rho =T
ρ=T。在回波中,间隔大于这一时间的两个目标都不会被同一脉冲同时照射到。因此,好分辨率=短脉冲。
但为了得到精确的目标参数,SNR要高,即平均发射功率要大。增大平均发射功率可以通过增大峰值功率或发射信号长度(持续时间)实现,加峰值很难,所以一般加长度。经延伸后的信号长度一般远高于分辨率所需的脉冲长度。
所以,发送一个展宽脉冲后,对其回波进行脉冲压缩,以得到所需分辨率。
原理:
把宽的rect变窄的sinc
为了取得好的脉冲压缩,需要使接收信号的频谱幅度非常平坦,且相位仅包含常量和线性分量。
-
平坦:使线性调频信号均匀扫频,即通过时域相位的二次分量实现。如果发射线性调频信号,则其回波也为线性调频信号,符合平坦的条件:
线性调频信号:
s
(
t
)
=
rect
(
t
T
)
exp
{
j
π
K
t
2
}
s(t)=\operatorname{rect}\left(\frac{t}{T}\right) \exp \left\{j \pi Kt^{2}\right\}
s(t)=rect(Tt)exp{jπKt2};
线性调频信号频谱:
S
(
f
)
=
rect
(
f
K
T
)
exp
{
−
j
π
f
2
K
}
S(f)=\operatorname{rect}\left(\frac{f}{K T}\right) \exp \left\{-j \pi \frac{f^{2}}{K}\right\}
S(f)=rect(KTf)exp{−jπKf2}
-
线性相位:去掉线性调频信号频域相位的二次分量,即去掉
ϕ
(
f
)
=
−
π
f
2
K
\phi(f)=-\pi \frac{f^{2}}{K}
ϕ(f)=−πKf2。
线性调频信号回波符合平坦的条件,因此只需考虑去掉频域相位的二次分量。因此,为了得到线性相位的平坦频谱,可以设匹配滤波器为
H
(
f
)
=
rect
{
f
∣
K
∣
T
}
exp
{
+
j
π
f
2
K
}
H(f)=\operatorname{rect}\left\{\frac{f}{|K| T}\right\} \exp \left\{+j \pi \frac{f^{2}}{K}\right\}
H(f)=rect{∣K∣Tf}exp{+jπKf2}
再经过傅里叶逆变换就可以得到所需的sinc函数。
实现:
设调频信号回波为
s
r
(
t
)
=
rect
(
t
−
t
0
T
)
exp
{
j
π
K
(
t
−
t
0
)
2
}
s_{r}(t)=\operatorname{rect}\left(\frac{t-t_{0}}{T}\right) \exp \left\{j \pi K\left(t-t_{0}\right)^{2}\right\}
sr(t)=rect(Tt−t0)exp{jπK(t−t0)2}
分辨力为
ρ
=
T
\rho =T
ρ=T,信号频谱近似为
S
r
(
f
)
=
rect
{
f
∣
K
∣
T
}
exp
{
−
j
π
f
2
K
}
exp
{
−
j
2
π
f
t
0
}
S_{r}(f)=\operatorname{rect}\left\{\frac{f}{|K| T}\right\} \exp \left\{-j \pi \frac{f^{2}}{K}\right\} \exp \left\{-j 2 \pi f t_{0}\right\}
Sr(f)=rect{∣K∣Tf}exp{−jπKf2}exp{−j2πft0}
匹配滤波(即
S
r
(
f
)
乘
H
(
f
)
S_{r}(f)乘H(f)
Sr(f)乘H(f))后,频谱为
S
out
(
f
)
=
S
r
(
f
)
H
(
f
)
=
rect
{
f
∣
K
∣
T
}
exp
{
−
j
2
π
f
t
0
}
S_{\text {out }}(f)=S_{r}(f) H(f)=\operatorname{rect}\left\{\frac{f}{|K| T}\right\} \exp \left\{-j 2 \pi f t_{0}\right\}
Sout (f)=Sr(f)H(f)=rect{∣K∣Tf}exp{−j2πft0}
对
S
out
(
f
)
S_{\text {out }}(f)
Sout (f)进行傅里叶逆变换得到
s
out
(
t
)
=
∣
K
∣
T
sinc
{
K
T
(
t
−
t
0
)
}
s_{\text {out }}(t)=|K| T \operatorname{sinc}\left\{K T\left(t-t_{0}\right)\right\}
sout (t)=∣K∣Tsinc{KT(t−t0)}
通过下图频谱可以直观看到,间隔脉冲压缩的调频信号频域相位为线性相位。
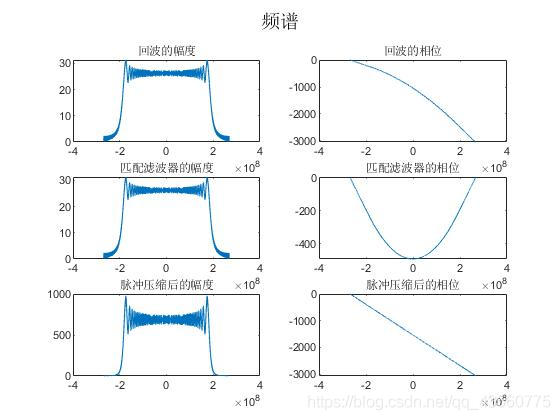
也可以在时域将回波直接与匹配滤波器卷积。匹配滤波器可以设为
s
(
t
)
s(t)
s(t)的复共轭
h
(
t
)
=
rect
(
t
T
)
exp
{
−
j
π
K
(
−
t
)
2
}
=
rect
(
t
T
)
exp
{
−
j
π
K
t
2
}
\begin{aligned} h(t) &=\operatorname{rect}\left(\frac{t}{T}\right) \exp \left\{-j \pi K(-t)^{2}\right\} \\ &=\operatorname{rect}\left(\frac{t}{T}\right) \exp \left\{-j \pi K t^{2}\right\} \end{aligned}
h(t)=rect(Tt)exp{−jπK(−t)2}=rect(Tt)exp{−jπKt2}
卷积得到脉冲压缩后的回波
s
out
(
t
)
=
s
r
(
t
)
⊗
h
(
t
)
=
∫
−
∞
+
∞
s
r
(
u
)
h
(
t
−
u
)
d
u
≈
T
sinc
(
K
T
(
t
−
t
0
)
)
\begin{aligned} s_{\text {out }}(t) &=s_{r}(t) \otimes h(t) \\ &=\int_{-\infty}^{+\infty} s_{r}(u) h(t-u) d u\\ &\approx T \operatorname{sinc}\left(K T\left(t-t_{0}\right)\right) \end{aligned}
sout (t)=sr(t)⊗h(t)=∫−∞+∞sr(u)h(t−u)du≈Tsinc(KT(t−t0))
得到匹配滤波后的脉冲
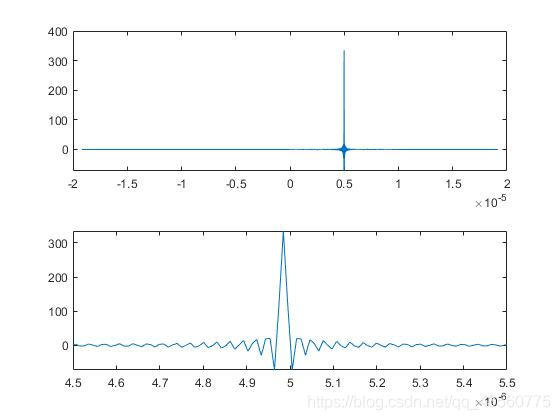
此时分辨率指脉冲信号中两个-3dB点之间的间隔,幅度峰值0.707倍处。压缩后信号频谱带宽为
∣
K
∣
T
|K| T
∣K∣T,则时间量纲下sinc函数第一个过零点为
1
∣
K
∣
T
\frac{1}{|K| T}
∣K∣T1,分辨率为
ρ
=
0.886
∣
K
∣
T
≈
1
∣
K
∣
T
\rho=\frac{0.886}{|K| T} \approx \frac{1}{|K| T}
ρ=∣K∣T0.886≈∣K∣T1
magic~
参考文献:《合成孔径雷达成像 算法与实现》