基础篇(二)
向量
点,向量和标量的区别
:
点是一个没有大小之分的空间中的位置
向量是一个有模有方向但是没有位置的量
标量是一个只有模没有方向的量
向量和向量的加法:
A+B = (Ax+bx,Ay+By)
向量和向量的减法:
A-B = (Ax-bx,Ay-By)
注意:向量不能和标量相加减,不能和维度不一样的向量相加减
向量和标量的除法:
A/a = (Ax/a,Ay/a)
向量和标量的乘法:
A
a = (Ax
a,Ay*a)
对于加减法:我们有三角形法则求距离
对于乘除法:我们可以求缩放
向量的模:
|A| = 每个分量的平方和然后开平方
向量的点积:
A.B = Ax.Bx+Ay.By+Az.Bz
意义:A点乘B向量代表B在A上面的投影,当结果大于0,方向为正,反之,方向为反
A.B=|A|.|B|.Cos@
我们可以通过角度的余弦值,来知道两个向量之间的方向关系
向量的叉积:
AxB = (AyBz-AzBy,AzBx-AxBz,AxBy-AyBx)
叉乘用来求垂直于AB平面的向量,求副切线
矩阵
矩阵在shader中的应用
:
float2 centerUV = float2(0.5,0.5);//中心点
float rotaNormalAngle =(_BumpAngle * PI)/180;//旋转角度
float CosNormalAngle = cos(rotaNormalAngle);//余弦值
float SinNormalAngle = sin(rotaNormalAngle);//正弦值
float2 uvnormal = (mul(float3(i.uvnormal-centerUV,1),float3x3(1,0,0,0,1,0,_BumpShiftX,_BumpShiftY,1))).xy;//这是处理uv坐标,所以使用的是3维的平移矩阵
uvnormal = mul(uvnormal,float2x2(_BumpRepeat,0,0,_BumpRepeat));//2维缩放矩阵
uvnormal = mul(uvnormal,float2x2(CosNormalAngle,-SinNormalAngle,SinNormalAngle,CosNormalAngle)) + centerUV;//2维旋转矩阵
矩阵是3D数学的重要基础,它主要用来描述两个坐标系统之间的关系,通过定义一种运算而将一个坐标系中的向量转换到另一个坐标系。
向量是标量的数组,矩阵是向量的数组
。
矩阵的维度
:
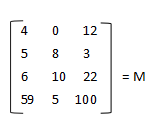
矩阵的维度被定义为它包含了多少行和多少列,上面这个矩阵为
4×3
的矩阵,我们表示矩阵当中的某个元素,一般用Mij来表示,i表示行,j表示列。
方阵
行数和列数相同的矩阵被称为是方阵
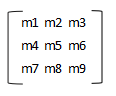
方阵行数和列数一样的元素被称为对角线元素,其他元素均为
非对角线元素
对角矩阵
:如果所有非对角线元素都为0
单位矩阵
:一种特殊的对角矩阵,n维单位矩阵记作In,是nxn的矩阵,对角线的元素为1,其他元素为0.单位矩阵非常特殊,他是矩阵的乘法单位元,基本性质是用任意一个矩阵乘以单位矩阵,都将得到原来的矩阵。
注意:
对角线的元素只有一条,并不包括另外一条
.
转置
:
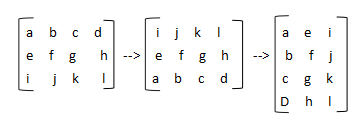
矩阵的转置就是把矩阵沿x轴旋转180度,然后沿z轴顺时针旋转90度
(书上写的沿着矩阵的对角线翻折)
定理
:
1.对于任意矩阵,将一个矩阵转置一次,再转置一次便会得到原来的矩阵,这条法则也适用于向量
2.对于任意对角矩阵,都有这个矩阵的转置矩阵等于它自己
矩阵的运算
:
矩阵和标量的乘法
:
矩阵M和标量k相乘
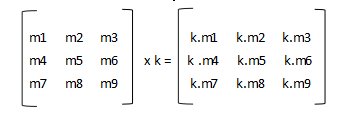
简而言之,就是用k去乘以矩阵中的每个元素,矩阵样式不变
矩阵与矩阵的乘法:
条件:
矩阵M和矩阵N相乘,M的行数必须和N的列数一样,否则,乘法无意义
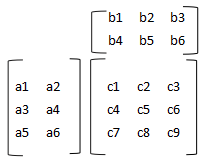
c1 = a1
b1 + a2
b4
行和列相乘
注意事项
:
矩阵乘法不满足交换律
矩阵乘法满足结合律
矩阵积的转置等于先转置矩阵然后以相反的方向乘
向量和矩阵的乘法
1.行向量左乘矩阵,结果是行向量
2.列向量右乘矩阵,结果是列向量
反之,则无定义
DirectX使用的是行向量
等式中使用列向量更好
OpenGL使用列向量
矩阵的几何解释
矩阵是如何变换向量的?
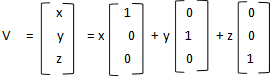
如果把矩阵的行解释为坐标系的基向量,那么乘以该矩阵就相当于执行了一次坐标变换,如果有aM =b,那么我们就说M将a转换到b.
矩阵的形式:
矩阵的每一行都能理解为转换之后的基向量
矩阵和线性变换:
变换物体和变换坐标系
变换物体:将一个物体顺时针旋转90度,意味着旋转物体上的点,坐标移动到了一个新的位置
变换坐标系:当我们旋转坐标系的时候,物体本身并没有移动,只是我们在另外一个坐标系中描述它
两种变换实际上是等价的,将物体变换一个量,等价于将坐标系变换一个相反的量
旋转矩阵的推导
:
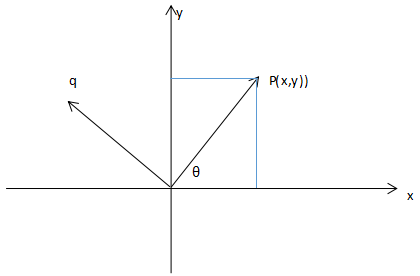
我们可以根据三角函数cosθ = x/斜边,而且我们知道斜边的长度为1,所以x = cosθ
同理y = sinθ,因此p点的坐标可以表示为p(cosθ,sinθ).
同理,我们也可以用三角函数求得q的坐标q(-sinθ,cosθ).
然后我们可以组合一个2D的旋转矩阵

这里只是列举了2d旋转矩阵的推导,3d的旋转矩阵也差不多,只不过绕某个轴旋转的时候,保持这个轴不动就行。
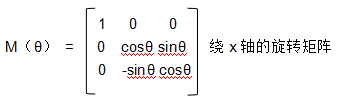
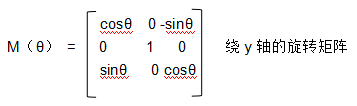
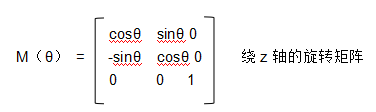

绕任意轴n,角度θ的旋转矩阵
缩放矩阵的推导:
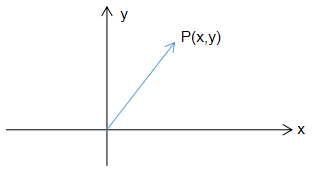
如果要对p点进行缩放,那么我们直接改变的就是在p的基础坐标上进行缩放,只需要在p的坐标乘或者除以某个系数既可
由此我们可以推导二维缩放矩阵:
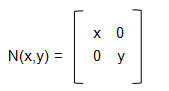
矩阵N对二维向量进行缩放,缩放系数为x,y
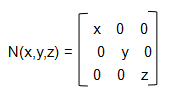
扩充的三维缩放矩阵
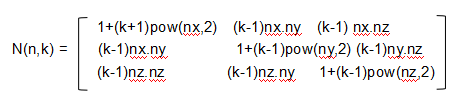
沿着3d任意轴的缩放矩阵,n为方向,k为缩放因子
平移矩阵
平移不属于线性变换
因为平移不会改变方向,所以我们需要增加一个维度,对当前的向量进行平移操作