西瓜书第七章习题及答案

学习笔记：

给定某系统的若干样本x，计算该系统的参数即，

条件概率公式：P(c |x) =

(

∣

)

∗

(

)

(

)

\frac{P(x|c)*P(c)} {P(x)}

$\frac{P ( x ∣ c ) * P ( c )}{P ( x )}$

p（c）：没有数据支持下，θ发生的概率———–

先验概率

。

类先验概率P(c）表达了样本主问中各类样本所占的比例?根据大数定律，当训练集包含充足的独立同分布样本时P(c）可通过各类样本出现的频率来进行估计。

p(c|x)：在数据x的支持下，θ发生的概率———–

-后验概率

。

p(x|c)：给定某个参数θ的概率分布——————–

类条件概率或者似然函数

。

对类条件概率 P(x I c) 来说，由于它涉及关于所有属性的联合概率，直接根据样本出现的频率来估计将会遇到严重的困难。

7.1

在这里插入图片描述
数据集：

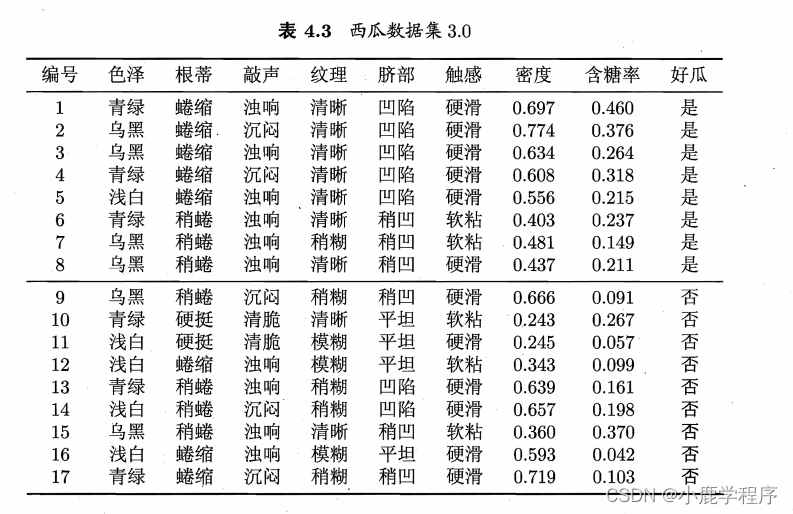
关于类别c的类条件概率（就是把类别当条件）为P(x | c)，设P(x | θ)具有确定形式并且被参数

θ_c

$θ_{c}$

唯一确定，为了方便我们将P(x | θ)记作P(x |

θ_c

$θ_{c}$

)。

解答，对于表4.3有：：

好瓜=是共有八条数据，（对于色泽）包括：青绿-3个、乌黑-4个、浅白-1个。

好瓜=否共有九条数据，（对于色泽）包括：青绿-3个、乌黑-2个、浅白-4个。

根据类条件概率P(x | c)有（根据表格直接得出-对应P151公式(7.17)）：

P(色泽=青绿 | 好瓜=是) =

\frac{3}{8}

$\frac{3}{8}$

P(色泽=乌黑 | 好瓜=是) =

\frac{4}{8}

$\frac{4}{8}$

P(色泽=浅白 | 好瓜=是) =

\frac{1}{8}

$\frac{1}{8}$

对于每一行数据（向量）记:

P(色泽=青绿 | 好瓜=是) =

λ_1

$λ_{1}$

P(色泽=乌黑 | 好瓜=是) =

λ_2

$λ_{2}$

P(色泽=浅白 | 好瓜=是) = 1-

λ_1

$λ_{1}$

–

λ_2

$λ_{2}$

，

根据P149公式(7.9)有:

P(

好瓜

是

D_{好瓜=是}

$D_{好瓜 = 是}$

|

好瓜

是

θ_{好瓜=是}

$θ_{好瓜 = 是}$

) =

∈

(

∣

好瓜

是

)

\displaystyle\prod_{\boldsymbol{x}∈D_c} P(x|θ_{好瓜=是})

$x \in D_{c} \prod P (x ∣ θ_{好瓜 = 是})$

=

λ_1^3

$λ_{1}^{3}$

λ_2^4

$λ_{2}^{4}$

(1-

λ_1

$λ_{1}$

–

λ_2

$λ_{2}$

)

)

(1)

$(1)$

再根据公式（7.10）LL(

θ_c

$θ_{c}$

) = log P(

∣

D_c | θ_c

$D_{c} ∣ θ_{c}$

) =

∈

(

∣

)

\displaystyle\sum_{x∈D_c} logP(x|θ_c)

$x \in D_{c} \sum l o g P (x ∣ θ_{c})$

)

(2)

$(2)$

将(1)带入(2)中得到：

LL(

θ_c

$θ_{c}$

) = 3log

λ_1

$λ_{1}$

+ 4log

λ_2

$λ_{2}$

+ log(1-

λ_1

$λ_{1}$

–

λ_2

$λ_{2}$

),

根据这个式子分别对

λ_1

$λ_{1}$

、

λ_2

$λ_{2}$

求偏导数为0时的值，有

λ_1

$λ_{1}$

=

\frac{3}{8}

$\frac{3}{8}$

，

λ_2

$λ_{2}$

=

\frac{4}{8}

$\frac{4}{8}$

， 1-

λ_1

$λ_{1}$

–

λ_2

$λ_{2}$

=

\frac{1}{8}

$\frac{1}{8}$

。

同理

好瓜=否共有九条数据，（对于色泽）包括：青绿-3个、乌黑-2个、浅白-4个：

P(色泽=青绿 | 好瓜=否) =

μ_1

$μ_{1}$

P(色泽=乌黑 | 好瓜=否) =

μ_2

$μ_{2}$

P(色泽=浅白 | 好瓜=否) = 1-

μ_1

$μ_{1}$

–

μ_2

$μ_{2}$

，

根据P149公式(7.9)有:

P(

好瓜

否

D_{好瓜=否}

$D_{好瓜 = 否}$

|

好瓜

否

θ_{好瓜=否}

$θ_{好瓜 = 否}$

) =

∈

(

∣

好瓜

否

)

\displaystyle\prod_{\boldsymbol{x}∈D_c} P(x|θ_{好瓜=否})

$x \in D_{c} \prod P (x ∣ θ_{好瓜 = 否})$

=

μ_1^3

$μ_{1}^{3}$

μ_2^2

$μ_{2}^{2}$

−

)

(1- μ_1-μ_2)^4

$(1 - μ_{1} - μ_{2})^{4}$

,

LL(

θ_c

$θ_{c}$

) = 3log

μ_1

$μ_{1}$

+ 2log

μ_2

$μ_{2}$

+ 4log(1-

μ_1

$μ_{1}$

–

μ_2

$μ_{2}$

),

根据这个式子分别对

μ_1

$μ_{1}$

、

μ_2

$μ_{2}$

求偏导数为0时的值，有

μ_1

$μ_{1}$

=

\frac{3}{9}

$\frac{3}{9}$

，

μ_2

$μ_{2}$

=

\frac{2}{9}

$\frac{2}{9}$

， 1-

μ_1

$μ_{1}$

–

μ_2

$μ_{2}$

=

\frac{4}{9}

$\frac{4}{9}$

。

解答只写了色泽属性，其余属性求解方法一样。

7.3

在这里插入图片描述

拉普拉斯修正中的公式就是在公式（7.17）上做了一些改变，，拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题。

import numpy as np
import pandas as pd
import math

#准备数据阶段
def readData():         
    dataset = pd.read_excel('F:\\python\\dataset\\chapter5\\watermaton3a.xlsx')  # 读取数据
    Attributes = dataset.columns[1:]    # 属性名称列表
    dataset = np.array(dataset)
    dataset = dataset[:,1:]
    m,n = np.shape(dataset)
    dataList = []
    for i in range(m):      # 生成数据列表，列表元素是集合类型
        curset = {}
        for j in range(n):
            curset[Attributes[j]] = dataset[i,j]
        dataList.append(curset)
 
    attrNum = {}            # 统计每个属性的可取值个数
    for i in range(n):
        curSet = set()      # 使用集合是利用了集合里面元素不可重复的特性，从而提取出了每个属性的取值
        for j in range(m):
            curSet.add(dataset[j,i])
        attrNum[Attributes[i]] = len(curSet)
    return dataList,attrNum

#拉普拉斯修正的类先验概率
def getClassPrior(classname,classvalue,dataset,attrNum):     
    count = 0
    for i in range(len(dataset)):
        if dataset[i][classname] == classvalue : count += 1
    return (count+1)/(len(dataset) + attrNum[classname])

## 得到类条件概率
def getClassCondition(classname,classvalue,classCondname,classCondvalue,dataset,attrNum):   
    if classname=='密度'or classname=='含糖率':      # 若是连续属性，则用概率密度进行计算
        value = []
        for i in range(len(dataset)):
            if dataset[i][classCondname]==classCondvalue:
                value.append(dataset[i][classname])
        mean = np.mean(value)
        delt = np.std(value)
        return (1/(math.sqrt(2*math.pi)*delt))*math.exp(-(classvalue-mean)**2/(2*delt**2))
    else:                                             # 离散属性用频率代替概率，并进行拉普拉斯平滑
        count = 0
        count_ = 0
        for i in range(len(dataset)):
            if dataset[i][classname]==classvalue and dataset[i][classCondname]==classCondvalue:
                count += 1
            if dataset[i][classCondname]==classCondvalue : count_ += 1
        return (count+1)/(count_+attrNum[classname])

if __name__ == '__main__':
    test1 = {'色泽':'青绿','根蒂':'蜷缩','敲声':'浊响','纹理':'清晰','脐部':'凹陷','触感':'硬滑',\
         '密度':0.697,'含糖率':0.460}
    dataset,attrNum = readData()
    Pgood = getClassPrior('好瓜','是',dataset,attrNum)
    Pbad = getClassPrior('好瓜','否',dataset,attrNum)
    for i in test1:
        Pgood *= getClassCondition(i,test1[i],'好瓜','是',dataset,attrNum)
        Pbad *= getClassCondition(i,test1[i],'好瓜','否',dataset,attrNum)
    print(Pgood,Pbad)
    print('该西瓜是%s'%('好瓜' if Pgood>Pbad else '坏瓜'))

实验结果：

在这里插入图片描述

7.3代码参考链接


参考链接

原文链接：https://blog.csdn.net/qq_43761012/article/details/126051479

学习笔记：

7.1

7.3

你可能也喜欢