目录
(注:借鉴蓝桥杯国赛特训营)
一、字典树算法的概念介绍
首先我们看下字典的组织方式
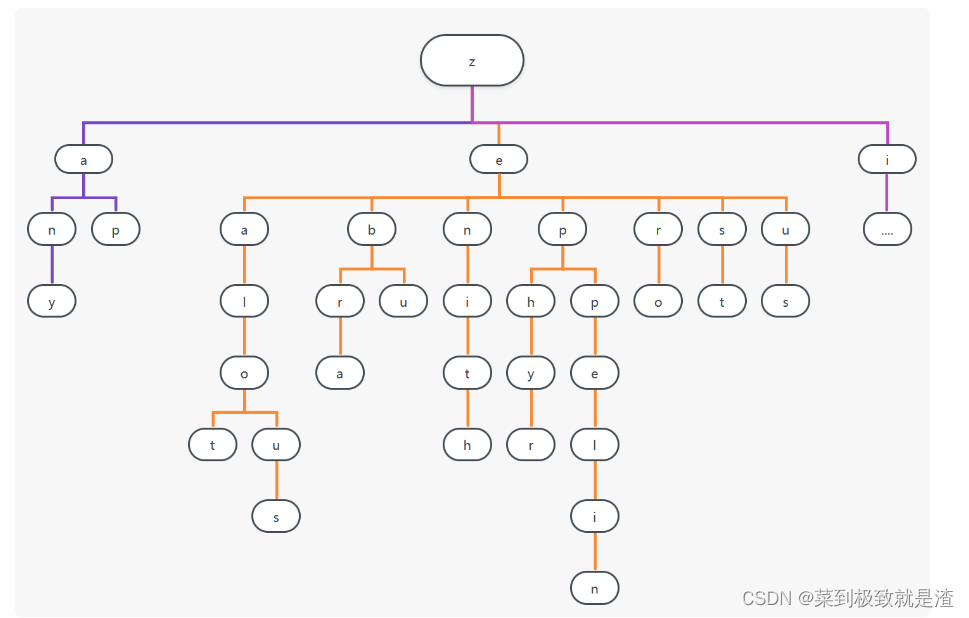
Trie 的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
我们的字典树也是这样的结构,我们如何组织呢?
字典树的组织方式有哪些?
插入
查询
删除
修改
1. 插入:
字典树的插入,就是将一个单词,插入到现有的字典中,每一个单词的关键字就是他的字符。
每次插入都要从根节点开始进行。
根据自身关键字继续向下进行,如果匹配到就沿着匹配到的曾经创建过的分支往下继续匹配关键字。
根据自身关键字向下进行,如果匹配失败就按照自己的关键字创建分支。
重复 2,3 直至自身遍历结束。
2. 查询:
字典树的查询就是判断,该单词是否被字典树包含。
与插入一样,从根节点开始,按照自身关键字,选择路径。
不同的是,遇到匹配失败时,返回没有找到,并不创建新的节点。
并且,当关键字用完后,返回查找成功。
3. 删除和修改:
然而删除和修改是不存在的,因为你不知道这个节点是不是自己创建的,是不是还有其他单词在使用,所以我们不能贸然的删除这一个节点。
对于需要删除和修改的,我给出一个方向,对于某个节点我们可以记录访问次数,来代表多少个单词使用过该节点,就能进行删除和修改操作。
当然不在我们本节课的知识范畴内,这种桶排计数加字典树的方式还是比较简单的。
根据我们所构思的字典树,我们可以自己写出代码。
我们依旧使用数组模拟不使用链表的方式。
二、字典树算法的实现
#include <bits/stdc++.h> using namespace std; //字典树算法 int trie[10000][30];// bool end[10000];//判断该层数是否结尾 int tot=1; //插入 void insert(string str) { int len=str.size(); int p=1; for(int k=0;k<len;k++){ int ch=str[k]-'a'; if(trie[p][ch]==0){ trie[p][ch]=++tot; } p=trie[p][ch]; } end[p]=true; } //检索 bool search(string str) { int len=str.size(); int p=1; for(int k=0;k<len;k++){ p=trie[p][str[k]-'a']; if(p==0){ return false; } } return end[p]; }
三、例题
(爱找事的小Z)题目描述:
小 Z 同学非常喜欢找事,现在有很多名为“事”的字符串,现在小 Z 想要找“事”,请你帮助他判断,他今天是否找了两件相同的事。
数据范围:
事的输入量不超过10^4,每个"事"字符串的长度不超过1000,且所有字母均为小写。
他看到了两个字符串 s1 s2 ,他想知道 S1 在 S2 中出现了多少次。
输入描述:
第一行输入 n ,为小 z 今天找了多少事
然后,共输入n行
第一行为 事1
第二行为 事2
....
输出描述:
是否找到了两件相同的事,相同输出 1,没有相同的就输出 0
输入输出样例:
- 样例 1:
Input:
12
acd
acd
asdfsdf
asd
f
saf
asdf
sfasdfs
f
asdf
asf
asdfs
output:
1
- 样例 2:
Input:
21
adfasdfaasdf
asdfsfas
fa
sdfasd
fsd
fs
a
sda
fsd
afasd
f
sda
f
asdf
as
df
sda
gggggas
dfdsfe
def
a
output:
1#include<bits/stdc++.h> using namespace std; int trie[1000010][30]; int tot=1; bool endstr[1000010]; int n; //插入 void insert(string str) { int len=str.size(),p=1; for(int k=0;k<len;k++){ int ch=str[k]-'a'; if(trie[p][ch]==0){ trie[p][ch]=++tot; } p=trie[p][ch]; } endstr[p]=true; } //检索 bool search(string str) { int len=str.size(),p=1; for(int k=0;k<len;k++){ p=trie[p][str[k]-'a']; if(p==0){ return false; } } return endstr[p]; } int main() { cin>>n; string s; int ans=0; for(int i=0;i<n;i++){ cin>>s; if(search(s)){ ans++; } else{ insert(s); } } if(ans){ cout<<"1"; } else{ cout<<"0"; } return 0; }