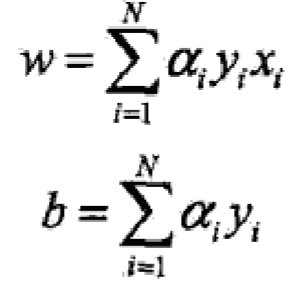感知机是二分类的线性分类模型,其输入为实例的特征向量,输出为类别。
2.1 感知机模型
对应与输入空间的点,感知机输出的是这正负两类分离超平面,由输入空间到输出空间的如下函数:
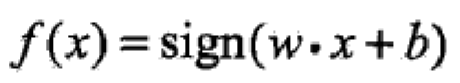
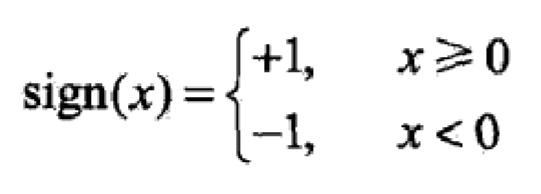
感知机的几何解释:
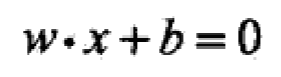
这是特征空间中的一个超平面(或者叫决策边界),它把特征空间分割成两部分,一部分中全是正例,另一部分中全是反例。

如图为两个特征的感知机模型,直线wx+b=0是分离超平面,
因为当x等于任意值时,把w带入(wx+b)中都是等于0的,所以向量w垂直与分离超平面(wx+b = 0)。
2.2 感知机学习策略
如果存在某个超平米能够将数据集的正实例点和负实例点完全正确的划分到超平米的两侧则将该数据集T称为线性可分数据集
损失函数可以表示为误分类点到平米的距离:
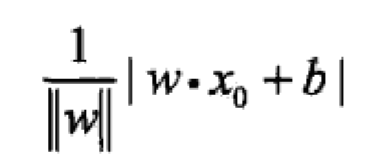
上式去掉绝对值变成:
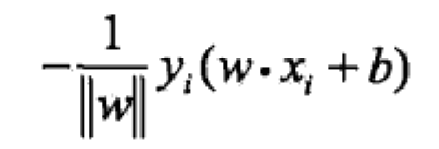
(这个式子在只考虑误分类点的情况下是 >= 0的)
那么,假设超平面S的
误分类
点集合为M,那么所有误分类点到超平面S的总距离为:
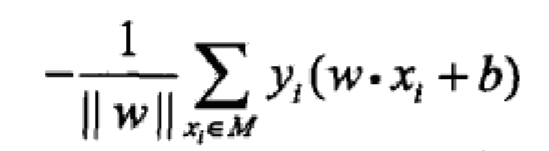
再忽略掉w的二范数,感知机的损失变为:
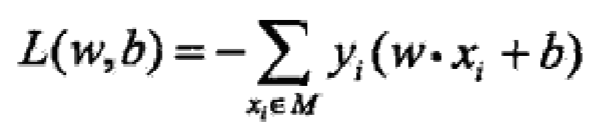
2.3 感知机的学习算法
感知机的学习算法(降低损失函数,找到最优模型的过程)包括原始形式和对偶形式。
2.3.1 感知机学习算法的原始形式
问题:
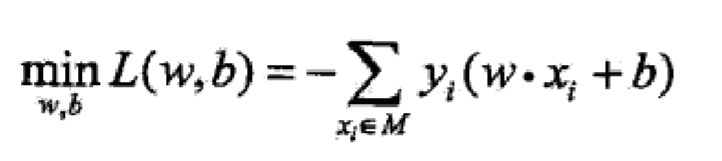
感知机学习算法是误分类点(
上式中的M
)驱动的,具体采用随机提督下降法(stochastic gradient descent)。首先选取任意超平米w0 , b0 。然后用梯度下降法不断极小化损失函数。极小化过程中不是使所有误分类点到梯度下降,而是一次随机选取一个点使其梯度下降。
损失函数对w和b求偏导可得到:

随机选取一个误分类点(xi , yi),对w,b进行更新:

(n为学习率)
学习步骤:

""""
作业二:
1:思考感知机模型的假设空间是什么?模型复杂度提现在哪里?
答:
(1)感知机模型的假设空间是由不同的w ,b取值所形成的不同的 wx+b=0 的超平面组成的。
(2)模型复杂度在于高维向量内积的计算量巨大
2:已知训练数据集D,其正实例点是x1=(3,3)T,x2=(4,3)T,负实例点是x3=(1,1)T:
(1) 用python 自编程实现感知机模型,对训练数据集进行分类,并对比误分类点选择次序不同对最终结果的影响。可采用函数式编程或 面向对象的编程。
(2)试调用sklearn.linear_model 的Perceptron模块,对训练数据集进行分类,并对比不同学习率h对模型学习速度及结果的影响。
(3)附加题:对比传统感知机算法及其对偶形式的运行速度。
"""
#传统感知机算法实现
import numpy as np
train = np.array([[3,3,1],[4,3,1],[1,1,-1]])
w = [0,0]
b = 0
print(train)
def loss(point,w,b):
return -(point[2] * (point[0]*w[0] + point[1]*w[1] + b))
#学习率
a = 0.5
count = 0
while True:
if count == 3:
break
else:
count = 0
for i in range(train.shape[0]):
point = train[i]
l = loss(point,w,b)
print(point,l)
if l >= 0:
w[0] = w[0] + a*point[0]*point[2]
w[1] = w[1] + a*point[1]*point[2]
b = b + a*point[2]
print("w = ",w," b = ",b)
else:
count += 1
print("w = ",w," b = ",b)
输出:
[[ 3 3 1]
[ 4 3 1]
[ 1 1 -1]]
[3 3 1] 0
w = [1.5, 1.5] b = 0.5
[4 3 1] -11.0
[ 1 1 -1] 3.5
w = [1.0, 1.0] b = 0.0
[3 3 1] -6.0
[4 3 1] -7.0
[ 1 1 -1] 2.0
w = [0.5, 0.5] b = -0.5
[3 3 1] -2.5
[4 3 1] -3.0
[ 1 1 -1] 0.5
w = [0.0, 0.0] b = -1.0
[3 3 1] 1.0
w = [1.5, 1.5] b = -0.5
[4 3 1] -10.0
[ 1 1 -1] 2.5
w = [1.0, 1.0] b = -1.0
[3 3 1] -5.0
[4 3 1] -6.0
[ 1 1 -1] 1.0
w = [0.5, 0.5] b = -1.5
[3 3 1] -1.5
[4 3 1] -2.0
[ 1 1 -1] -0.5
w = [0.5, 0.5] b = -1.5
2.3.2 感知机学习算法的对偶形式
感知机学习算法的原始形式和对偶形式与支持向量机学习算法的原始形式和对偶形式相对应。
对偶形式的基本想法是,将w和b标记为实例xi和标记yi的线性组合形式,用过求解其系数得到w和b 。可假设初始值w0 和 b0 均为0 。对误分类点(xi,yi)通过
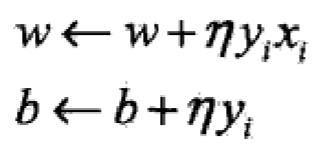
逐步修改w 和b,假设修改n次,则w ,b 的增量分别为 a·y·x 和 a·y,a = n * learning rate
这样,最后的w 和 b就可以表示为: