什么是图
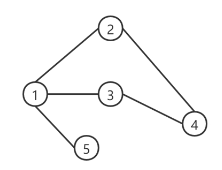
图的基本示意图
图是描述复杂事务的数据表示形式,由节点和边组成,数学上一般表述为
图G-(V,E)。其中的V(vertical)代表节点,可被理解为事物。
而E(edge)代表边,描述的是两个事物之间的关系。例如一个图的社交网络图,每个人都可视为节点,而人与人之间的关系可被视为边。
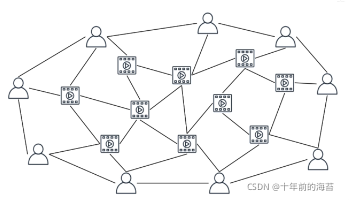
而在我们的推荐系统中,用户与物品之间的交互关系,用户与用户自身的关系,物品与物品之间的关系,完全可由一张图完整的进行描述。如下图所示:
用户与物品之间的关系图
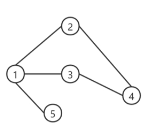
无向图与有向图
无向图
有向图
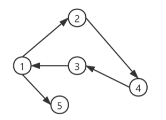
双向图
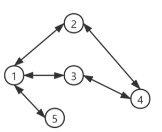
无向图是由没有方向的无向边组成的图,而有向图是由具有方向的有向边组成的图,有向边的出发节点称为
头节点
,结束节点则称为
尾节点
,无向图与双向图等价
有向有环图和无向无环图
有向有环图
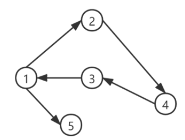
有向无环图
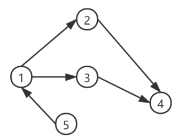
上图展示了有向有环图与有向无环图的区别,环是一种特殊的有向图,例如上方图中的1,2,3,4节点,1->2->4->3->1即形成一个环。在环中的任意节点经过边游走都能回到自身.
如果在一个有向图中没有任何一个节点经过边游走能回到自身,则便是有向无环图。即下面的图
无权图与有权图
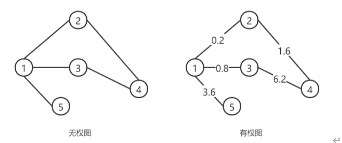
无权图指边没有权重,有权图只边带有权重
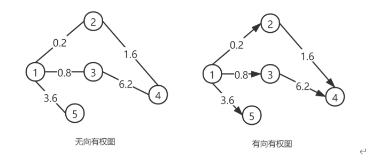
同构图和异构图
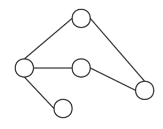
同构图

异构图
图的表示
1.邻接矩阵
虽然图在人类眼中可以很自观的展示出信息,但是对于计算机来讲,就不是那么容易理解了。所以我们需要研究图如何在计算机中表示。
邻接矩阵(Adjacency Matrix)是一种最基础的图表示方式。假设一个图的节点数量为N,则生成一个N*N的矩阵。矩阵中的值为对应位置节点与节点之间的关系,一般用A表示。
场景1:无向图
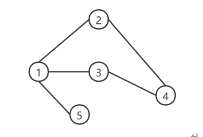

在一个基础的无向图中,若节点i与节点j有边连接,则在邻接矩阵的对应位置赋值1即可,记作A
ij
=A
ji
=1,否则为0。如上图所示,比如节点1与节点2右边相连,所以A
12
和A
21
的位置为1。无向图的邻接矩降是一个以对角矩阵镜像对称的矩阵。
场景2: 有向图
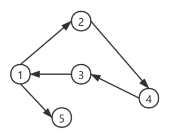

对于一个有向图,邻接矩阵不是对称矩阵,我们将邻接矩阵的行索引代表有向图中有向边的头节点,列索引代表尽节点。那么如果有边i->j,则A
ij
=1,A
ji
不再为1,除非连接i和j是一条双向边
场景3:有权图
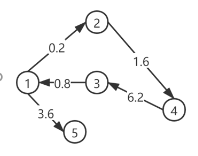

有权图的邻接表与无权图的唯一区别就是将边的权重代替了原来1的位置。
值得提的是,所有邻接矩阵的对角线均为0,因为对角线其实代表了节点与自身的关系,而节点与自身并无边相连,所以为0。
另外异构图的图表示方法略微复杂一点,我们具体放在后面讲。
2.邻接列表
场景1:无权图
将一张图以矩阵的形式表示固然非常使于计算,但是对于稀疏的人图非常不友好。而邻按列表的表示方式对于稀疏人图则非常友好。
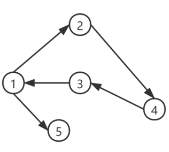
1:2,5
2:4
3:1
4:3
场景2:有权图
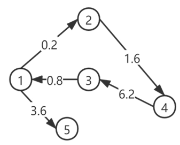
key: value
1: [(2,0.2), (5,3.6)]
2: [(4, 1.6)]
3: [(1,0.8 )]
4:[(3,6.2)]
3.边集
边集就更的简单,通常用两个头尾节点的索引元组表示一条边。例如头节点是h,尾节点是t:那么这一条有向边就是(b, t),如果是一条无向边则就用一对对称元组表示,即(h, t), (t, h)
场景1:有向无权图
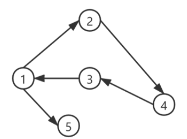
(1, 2),
(1,5),
(2.4),
(4.3),
(3,1)
场景2:无向无权图
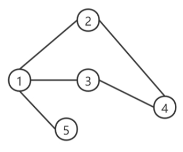
(1,2),
(2,1),
(1,5),
(5.1),
(2.4),
(4,2),
(4.3),
(3, 4),
(3,1),
(1.3)
场景3:有权图
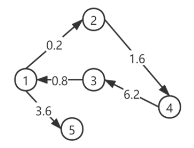
(1.0.2.2),
(1,3.6.5),
(2, 1.6.4),
(4,6.2,3),
(3,0.8,1)
邻居与度
节点的邻居(neighbor)指的是与该节点在同一边另一端的节点。
节点的度(degree)指的是该节点邻居的数量.
场景1:无向图
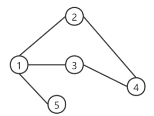
节点1:
邻居(neighbor)= 2,3,5
度(degree)- 3
节点2:邻居(neighbor)-1,4
度(degree)=2
场景2:有向图
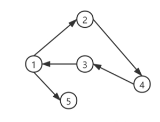
节点1:
前继邻居(predecessor)-3
后继邻居(successor)= 2,5
入度(indegree)= 1
出度(outdegree)= 2
结构特征、节点特征、边特征
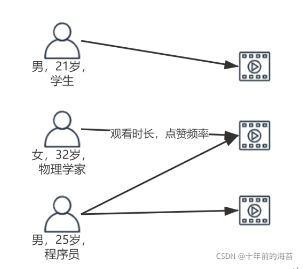
用户物品特征图
如上图所示,该图表示的是推荐场景中常有的用户与物品交互关系图。整个图即代表结构特征,本章目前讨论到现在也仅是在讨论图的结构特征
图由节点与边组成,对于节点来说,本身也可以带有一些特征或属性,例如上图中的用户画像特征。当然对于边同理,如上图的观看时长或点赞频率,边特征有时也叫关系特征:边的权重也可视为特征。
在机器学习与深度学习时,经常会对内容进行嵌入(embedding)操作,由嵌入操作得到的节点向量与边向量也可视为它们的特征.
处理图的库
1. NetworkX
Networks是最老牌的图处理库,早在2002年就发布了第一版,对于专门学习图算法的同学一定不陌生。简单易用,实现了一些基础的图算法。例如最小路径算法,最小权重生成树算法等。
https://www.osgeo.cn/networkx/tutorial.html
2.DGL(Deep Graph Library)
2.DGi(第一版发布于2018年,亚马逊继MxNet后又一力作,基于深度学习框架的图神经网络库,实现了主流的图神经网络算法。兼容MxNet,PyTorch,Tensorlow, 有中文的官方教程。是目前最主流的处理图的python APl
https://docs.dgl.ai/en/latest/guide_cn/index.html
PGL(Paddle Graph Learning)
3.PGL(Paddle Graph Learning),第一版发布于2020年,百度发布的国人之光框架,号称速度是DGL的13倍,使用与上手更容易。并且集成了百度自研的高效算法。但有一个致命的缺点,就是只兼容百度自家的飞浆(PaddlePaddle)深度学习框架。不知未来是否公与MxNet,PyTorch等兼容。