#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
int st[10000];
int vis[10];
typedef pair<int, int> PII;
PII way[10];
int path[10][10];
int c[10][10];
void dfs(int x){
if(x>n){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(c[i][j])cout<<"Q";
else cout<<".";
}
cout<<endl;
}
cout<<endl;
return;
}
for(int i=1;i<=n;i++){
if(!vis[i]){
c[x][i]=1;
vis[i]=1;
if(!st[x+i]&&!st[100+i-x]){
st[x+i]=st[100+i-x]=1;
dfs(x+1);
st[x+i]=st[100+i-x]=0;
}
vis[i]=0;
c[x][i]=0;
}
}
}
int main(){
cin>>n;
dfs(1);
}
#include <iostream>
#include <cstring>
#include <algorithm>
#include<queue>
using namespace std;
int n,m;
int a[101][101];
int vis[101][101];
int dp[101][101];
int xx[]={1,0,-1,0};
int yy[]={0,1,0,-1};
struct p{
int x;
int y;
int s;
};
queue<p>q;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)cin>>a[i][j];
}
q.push({1,1,0});
memset(dp,-1,sizeof dp);
dp[1][1]=0;
int ans=100000;
while(!q.empty()){
auto t=q.front();
q.pop();
int x=t.x;
int y=t.y;
int s=t.s;
if(x==n&&y==m)ans=min(ans,s);
for(int i=0;i<4;i++){
int dx=x+xx[i];
int dy=y+yy[i];
if(dx<1||dx>n||dy<1||dy>m)continue;
if(dp[dx][dy]==-1&&a[dx][dy]==0)
q.push({dx,dy,s+1}),
dp[dx][dy]=dp[x][y]+1;
}
}
cout<<dp[n][m]<<endl;
//cout<<ans;
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++)cout<<dp[i][j]<<" ";
// cout<<endl;
// }
}
八数码这道题很难想
就是把状态定义好区分好
然后用unordered_map
它的底层是用hash实现的查询复杂度是1
map的底层是红黑树实现的查询复杂度是logn
这道题目相当于//有很多状态,给定起点和终点求最短路;
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;
int xx[]={1,0,-1,0};
int yy[]={0,1,0,-1};
int bfs(string start){
unordered_map<string,int>d;
d[start]=0;
queue<string>q;
q.push(start);
string end="12345678x";
while(q.size()){
auto t=q.front();
q.pop();
if(t==end)return d[t];
int k=t.find('x');
int x=k/3;
int y=k%3;
int now=d[t];
for(int i=0;i<4;i++){
int dx=x+xx[i];
int dy=y+yy[i];
if(dx<0||dx>=3||dy<0||dy>=3)continue;
swap(t[k],t[3*dx+dy]);
if(!d.count(t))q.push(t),d[t]=now+1;
swap(t[k],t[3*dx+dy]);
}
}
return -1;
}
int main(){
string s;
for(int i=1;i<=9;i++){
char c;
cin>>c;
s+=c;
}
cout<<bfs(s);
}
给定一颗树,树中包含 n 个结点(编号 1∼n)和 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n,idx;
const int N = 2e5+10;
int h[N],ne[N],e[N],st[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int ans=0x3f3f3f3f;
int dfs(int u){
int sum=1,res=0;
st[u]=1;
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(!st[j]){
int s=dfs(j);
sum+=s;
res=max(res,s);
}
}
res=max(res,n-sum);
ans=min(ans,res);
return sum;
}
int main(){
memset(h, -1, sizeof h);
cin>>n;
for(int i=1;i<n;i++){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs(1);
cout<<ans;
}
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5+10;
int h[N],e[N],ne[N],n,m,idx,q[N],st[N];
int rudu[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool topsort(){
int hh=1,tt=0;
for(int i=1;i<=n;i++)if(rudu[i]==0)q[++tt]=i;
while(hh<=tt){
int u=q[hh++];
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
rudu[j]--;//指向我的边数减一,入度--
if(rudu[j]==0)q[++tt]=j;//如果减到0了的话说明它前面的已经遍历完了,这个时候可以把它放进队列
}
}
if(tt==n)return 1;
else return 0;
}
int main(){
memset(h, -1, sizeof h);
cin>>n>>m;
while(m--){
int a,b;
cin>>a>>b;
add(a,b);
rudu[b]++;
}
if(topsort()){
for(int i=1;i<=n;i++)printf("%d ",q[i]);
}
else puts("-1");
}
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int n,m,idx,h[N],e[N],ne[N],dist[N],q[N];
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs(){
memset(dist,-1,sizeof dist);
int hh=1,tt=0;
q[++tt]=1;
dist[1]=0;
while(hh<=tt){
int u=q[hh++];
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(dist[j]==-1)dist[j]=dist[u]+1,q[++tt]=j;
}
}
return dist[n];
}
int main(){
memset(h, -1, sizeof h);
cin>>n>>m;
while(m--){
int a,b;
cin>>a>>b;
add(a, b);
}
cout<<bfs();
}
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1000100;
int h[N],w[N],e[N],ne[N],n,m,dist[N],st[N];
int idx;
typedef pair<int,int> PII;
priority_queue<PII,vector<PII>,greater<PII>>heap;
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int dj(){
memset(dist,0x3f,sizeof dist);
heap.push({0,1});
dist[1]=0;
while(heap.size()){
PII t=heap.top();
heap.pop();
int id=t.second;
if(st[id])continue;
st[id]=1;
for(int i=h[id];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]>dist[id]+w[i]){
dist[j]=dist[id]+w[i];
heap.push({dist[j],j});
}
}
}
if(dist[n]==0x3f3f3f3f)return -1;
return dist[n];
}
int main(){
cin>>n>>m;
memset(h, -1, sizeof h);
while(m--){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
cout<<dj()<<endl;
}
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], w[N], ne[N], idx;
int n, m;
queue<int> q;
int st[N], dist[N], cnt[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int spfa() {
memset(dist, 0x3f, sizeof dist);
for (int i = 1; i <= n; i++) {
q.push(i);
st[i] = true;
}
st[1] = true;
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
// 如果超过了n-1
// 根据抽屉原理,说明经过某个节点两次,则说明有环
if (cnt[j] >= n) return true;
if (!st[j]) {
st[j] = true;
q.push(j);
}
}
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
if (spfa()) puts("Yes");
else puts("No");
}
作者:松鼠爱葡萄
链接:https://www.acwing.com/solution/content/19391/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
其实 本质上 只需要 从 负权的边 开始 走就可以了 所以 dict 不需要初始化 因为 只有 负权边 才会使得dist 变小 当cnt记录的负权边数 >= n 时 就证明了 一定存在负权环路 否则 无法证明 一定存在 负权环路 只是 可能 纯在 负权环路
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 20010,M=2*N;
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[N];
bool st[N];
int cnt[N];
int n,m;
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(){
memset(dist,0x3f,sizeof 0x3f);
queue<int>q;
for(int i=1;i<=n;i++)q.push(i),st[i]=1;
//for循环全部放进队列里面
while(q.size()){
int t=q.front();
q.pop();
st[t]=0;//把t从队列里面删去
for(int i=h[t];~i;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n)return 1;
if(!st[j])st[j]=1,q.push(j);
}
}
}
return 0;
}
int main(){
cin>>n>>m;
memset(h, -1, sizeof h);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
if(spfa())puts("Yes");
else puts("No");
}
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 20010,M=2*N;
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[N];
bool st[N];
int cnt[N];
int n,m,k;
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa(){
memset(dist,0x3f,sizeof 0x3f);
queue<int>q;
for(int i=1;i<=n;i++)q.push(i),st[i]=1;
//for循环全部放进队列里面
while(q.size()){
int t=q.front();
q.pop();
st[t]=0;//把t从队列里面删去
for(int i=h[t];~i;i=ne[i]){
int j=e[i];
if(dist[j]>dist[t]+w[i]){
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n)return 1;
if(!st[j])st[j]=1,q.push(j);
}
}
}
return 0;
}
void solve(){
idx=0;
memset(h, -1, sizeof h);
cin>>n>>m>>k;
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
while(k--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,-c);
}
if(spfa())puts("Yes");
else puts("No");
}
int main(){
int T;
cin>>T;
while(T--)solve();
}
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 220,INF=0x3f3f3f3f;
int d[N][N];
int n,m,q;
void floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
d[i][j]=min(d[i][j] , d[i][k]+d[k][j]);
}
}
}
}
int main(){
cin>>n>>m>>q;
memset(d,0x3f,sizeof d);
for(int i=1;i<=n;i++)d[i][i]=0;
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
d[a][b]=min(d[a][b],c);
}
floyd();
while(q--){
int a,b;
scanf("%d%d",&a,&b);
if(d[a][b]>=INF/2)puts("impossible");
else cout<<d[a][b]<<endl;
}
}
#include<bits/stdc++.h>
using namespace std;
const int N = 200010;
int n,m;
int a,b,c,f[N],cnt,ans;
int find(int x){
if(f[x]==x)return x;
else return f[x]=find(f[x]);
}
struct edge{
int a,b,w;
bool operator<(const edge &t){
return w<t.w;
}
}edges[N];
void kruskal(){
sort(edges,edges+m);//将每条边按照权重从小到大排序
for(int i=0;i<n;i++)f[i]=i;//初始化并查集
for(int i=0;i<m;i++){
int a=edges[i].a;
int b=edges[i].b;
int w=edges[i].w;
a=find(a),b=find(b);
if(a==b)continue;//在同一个集合里面就continue
f[a]=b;//合并
cnt++;//边数+1
ans+=w;//最小生成树权重+w
}
if(cnt!=n-1)puts("impossible");
else cout<<ans;
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++){
cin>>a>>b>>c;
edges[i]={a,b,c};
}
kruskal();
}
优化prim算法mlogn
Kruskal算法nlogn
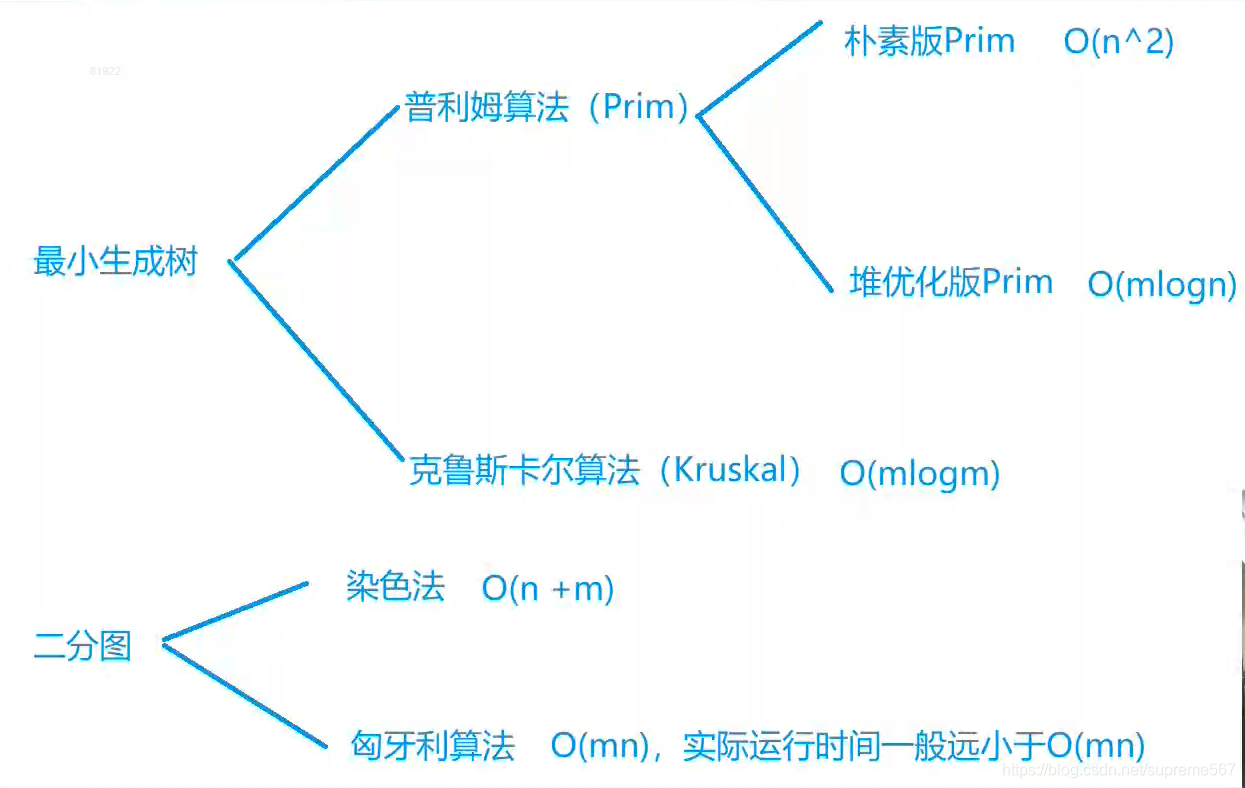
染色法m+n
匈牙利mn(实际运行远小于m*n
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+10,M=2e5+10;
int h[N], e[M], ne[M], idx;
void add(int a, int b) // 添加一条边a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int n,m;
int color[N];
bool dfs(int u,int c){
color[u]=c;
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(!color[j]){
if(!dfs(j,3-c))return 0;
}
else if(color[j]==c)return 0;
}
return 1;
}
int main(){
cin>>n>>m;
memset(h, -1, sizeof h);
while(m--){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
for(int i=1;i<=n;i++){
if(!color[i]){
if(!dfs(i,1)){
puts("No");
return 0;
}
}
}
puts("Yes");
return 0;
}
S 城现有两座监狱,一共关押着 N 名罪犯,编号分别为 1∼N。
他们之间的关系自然也极不和谐。
很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。
我们用“怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度,怨气值越大,则这两名罪犯之间的积怨越多。
如果两名怨气值为 c 的罪犯被关押在同一监狱,他们俩之间会发生摩擦,并造成影响力为 c 的冲突事件。
每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表,然后上报到 S 城 Z 市长那里。
公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。
在详细考察了 N 名罪犯间的矛盾关系后,警察局长觉得压力巨大。
他准备将罪犯们在两座监狱内重新分配,以求产生的冲突事件影响力都较小,从而保住自己的乌纱帽。
假设只要处于同一监狱内的某两个罪犯间有仇恨,那么他们一定会在每年的某个时候发生摩擦。
那么,应如何分配罪犯,才能使 Z 市长看到的那个冲突事件的影响力最小?这个最小值是多少?
输入格式
第一行为两个正整数 N 和 M,分别表示罪犯的数目以及存在仇恨的罪犯对数。
接下来的 M 行每行为三个正整数 aj,bj,cj,表示 aj 号和 bj 号罪犯之间存在仇恨,其怨气值为 cj。
数据保证 1≤aj<bj<N,0<cj≤109 且每对罪犯组合只出现一次。
输出格式
输出共 1 行,为 Z 市长看到的那个冲突事件的影响力。
如果本年内监狱中未发生任何冲突事件,请输出 0。
#include<bits/stdc++.h>
using namespace std;
const int N = 200010;
int n,m;
int p[N+N];
struct node{
int a,b,c;
bool operator<(const node &t){
return c>t.c;
}
}fanren[N];
int find(int x){
if(x==p[x])return p[x];
else return p[x]=find(p[x]);
}
int main(){
cin>>n>>m;
for(int i=0;i<n+n;i++)p[i]=i;
for(int i=0;i<m;i++)cin>>fanren[i].a>>fanren[i].b>>fanren[i].c;
sort(fanren,fanren+m);
for(int i=0;i<m;i++){
int x=find(fanren[i].a);
int y=find(fanren[i].b);
if(x==y){cout<<fanren[i].c;return 0;}
p[y]=find(fanren[i].a+n);
p[x]=find(fanren[i].b+n);
}
cout<<0;
return 0;
}
有两个集合 一个 f[1~n] 在这个范围 f[a] = b 说明 a和b 在一个监狱
还有一个集合 f[n+1 ~~~ n+n] f[a+n]=b 说明 a和b确定不在一个监狱
大佬解答里说了”首先我们将权值从大到小排序,然后对于每一对权值,如果说可以避免开,那么必须避免,因为我们的目的是让最大的影响力变得最小(这也是为什么,这道题目可以二分答案的原因,不过我们不需要).”
每个 a=find(a) b =find(b)
如果 a==b 那么说明前面有一些原因 明确了ab必须在同一个监狱(比如都不想和C在同一个监狱),那就输出已经确认了的关系和仇恨值.
如果a!=b 说明a b 不同源,他们仇恨值是当前最大,这个时候肯定把他们放在不同监狱
也就是后面的代码
fa[y]=find(e[i].a+n);//加入到下一个集合
fa[x]=find(e[i].b+n);//加入到下一个集合
作者:秦淮岸灯火阑珊
链接:https://www.acwing.com/solution/content/1001/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
(二分,染色法判断二分图) O((N+M)logC)O((N+M)logC)
将罪犯当做点,罪犯之间的仇恨关系当做点与点之间的无向边,边的权重是罪犯之间的仇恨值。
那么原问题变成:将所有点分成两组,使得各组内边的权重的最大值尽可能小。
我们在 [0,109][0,109] 之间枚举最大边权 limitlimit,当 limitlimit 固定之后,剩下的问题就是:
判断能否将所有点分成两组,使得所有权值大于 limitlimit 的边都在组间,而不在组内。也就是判断由所有点以及所有权值大于 limitlimit 的边构成的新图是否是二分图。
判断二分图可以用染色法,时间复杂度是 O(N+M)O(N+M),其中 NN 是点数,MM 是边数,可以参考AcWing 860. 染色法判定二分图。
为了加速算法,我们来考虑是否可以用二分枚举 limitlimit, 假定最终最大边权的最小值是 AnsAns:
那么当 limit∈[ans,109]limit∈[ans,109] 时,所有边权大于 limitlimit 的边,必然是所有边权大于 AnsAns 的边的子集,因此由此构成的新图也是二分图。
当 limit∈[0,ans−1]limit∈[0,ans−1] 时,由于 ansans 是新图可以构成二分图的最小值,因此由大于 limitlimit 的边构成的新图一定不是二分图。
所以整个区间具有二段性,可以二分出分界点 ansans 的值。二分算法模板可以参考这篇。
时间复杂度分析
总共二分 logClogC 次,其中 CC 是边权的最大值,每次二分使用染色法判断二分图,时间复杂度是 O(N+M)O(N+M),其中 NN 是点数,MM 是边数。因此总时间复杂度是 O((N+M)logC)O((N+M)logC)。
#include<bits/stdc++.h>
using namespace std;
const int N = 20010,M=200010;
int n,m;
int h[N], e[M], w[M], ne[M], idx;
int color[N];
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool dfs(int u,int c,int limit){
color[u]=c;
for(int i=h[u];~i;i=ne[i]){
if(w[i]<=limit)continue;
//凡是没有超过我这个限制的话都不用考虑
//否则放到另一个集合
//如果放到另一个集合里面ok的话就继续遍历u的下一条边
//否则直接返回false
int j=e[i];
if(!color[j]){
if(!dfs(j,3-c,limit))return 0;
}
else if(color[j]==c)return 0;
}
return 1;
}
bool check(int limit){
memset(color,0,sizeof color);
for(int i=1;i<=n;i++){
if(!color[i]){
if(!dfs(i,1,limit))return 0;
}
}
return 1;
}
int main(){
cin>>n>>m;
memset(h, -1, sizeof h);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a, b, c);
add(b, a, c);
}
int l=0,r=1e9;
while(l<r){
int mid=l+r>>1;
if(check(mid))r=mid;
else l=mid+1;
}
cout<<l;
}