一、曲线拟合简介
1、曲线拟合问题的提法
已知一组数据(二维),即平面上n个点 (xi,yi)(i=1,2,…,n), xi互不相同。寻求一个函数y=f(x),使得f(x)在某种准则下与所有的数据点最为接近,即拟合得最好。
2、线性最小二乘法
线性最小二乘法是解决曲线拟合最常用的方法,基本思路是,令
![]()
其中,r1(x),…,rm(x)是一组预先选定得一组线性无关的函数,a1,a2,…,am是待定系数.
涉及到的问题有二,一是系数确定;二是函数选取
2.1 系数确定
拟合准则:使得yi与f(xi)距离(称为残差)平方和最小,称为最小二乘法。,即
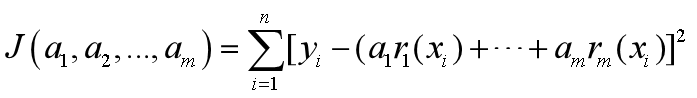
即求a1,…,am,转化为求J函数的最小值。
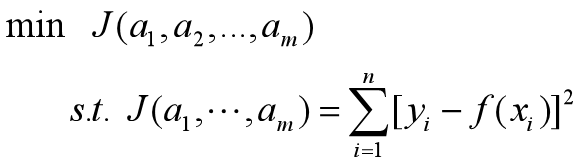
2.2 拟合函数的选取
拟合的前提是:
(1)通过机理分析,得到y和x的函数关系,这是r1(x),…, rm(x)也就好选取;
(2)若无法判断y和x的机理关系,绘制(xi,yi)的散点图,直观判断用什么曲线取拟合。
常用的曲线有
(1)线性
![]()
(2)多项式
![]()
(一般m=2,3)
(3)双曲函数(一支)

(4)指数曲线
![]()
一般需要几种曲线分别拟合,选最好的那个!
二、曲线拟合Matlab工具箱
1、多项式拟合(polyfit)
调用格式:a=polyfit(x0,y0,m)
x0,y0是数据向量,m表示多项式的阶数,返回的是多项式的降幂系数a=[a1,a2,…,am,am+1]。
polyfit
函数会根据给定的数据点
(x0, y0)
使用最小二乘方法进行拟合
,得到一个多项式模型,并返回其中的系数
a
。拟合多项式的阶数由参数
m
指定,表示拟合多项式的次数。返回的系数
a
是一个向量,其中的元素表示多项式中各项的系数,从高次项到低次项排列。例如,如果拟合多项式的阶数为 3,则
a
向量对应的是多项式
a(1)*x^3 + a(2)*x^2 + a(3)*x + a(4)
的系数。需要注意的是,
polyfit
函数会对数据进行拟合,尽可能地找到一个最佳的多项式模型来逼近数据点。选择适当的多项式阶数是重要的,
过高的阶数可能导致过拟合,而过低的阶数可能导致欠拟合。因此,在选择阶数时需要进行合理的权衡
。
要计算x处对应的多项式取值,需调用
y=polyval(a,x)
例如:
x0=1990:1:1996;
x1=x0-1989;
y0=[70,122,144,152,174,196,202];
a=polyfit(x1,y0,3)
0.7778 -11.7381 71.6270 12.5714
![]()
2、最小二乘曲线拟合
在 MATLAB 中,
lsqcurvefit
函数用于非线性最小二乘曲线拟合,可以通过拟合函数
fun
对给定的数据
(xdata, ydata)
进行拟合,并返回拟合后的参数
x
。
调用格式:x=lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
参数介绍:
fun
:拟合函数,可以是自定义函数或 MATLAB 内置函数。该函数应接受待拟合参数
x
和自变量
xdata
作为输入,并返回拟合函数对应的因变量值。
x0
:拟合参数的初始猜测值。这应该是一个向量。
xdata
:自变量数据,表示用于拟合的输入数据。这可以是一个向量、矩阵或多维数组。
ydata
:因变量数据,表示用于拟合的输出数据。这应该与
xdata
大小相同。
lb
:参数
x
的下界(可选)。这应该是一个向量。
ub
:参数
x
的上界(可选)。这应该是一个向量。
options
:优化选项(可选),用于控制拟合过程的参数和行为。
lsqcurvefit
函数
基于最小二乘法
,寻求使拟合函数的输出与实际数据之间的残差平方和最小化的最优参数
x
。它通过反复调整参数
x
的值,以改善拟合函数与数据之间的拟合效果。
在使用
lsqcurvefit
函数时,应提供适当的初始猜测参数
x0
,并根据需要设置参数的下界
lb
和上界
ub
。还可以通过
options
参数进一步控制拟合过程的行为,例如迭代次数、显示输出等。
举例理解lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options):
假设你有一组实验数据,表示物体从起始位置到时间的运动距离。你想要拟合一个非线性函数来描述物体的运动,具体为 y = a * exp(-b * x) + c * sin(d * x),其中 a、b、c、d是需要拟合的参数。
1. 拟合函数的定义:
function yfit = myFunction(x, p)
a = p(1);
b = p(2);
c = p(3);
d = p(4);
yfit = a * exp(-b * x) + c * sin(d * x);
end2. 定义初始猜测参数和参数范围:
x0 = [1, 0.1, 0.5, 2]; % 初始猜测参数
lb = [0, 0, 0, 0]; % 参数下界
ub = [Inf, Inf, Inf, Inf]; % 参数上界3. 加载实验数据:
load 'data.mat'; % 加载实验数据文件,假设包含 xdata 和 ydata4. 定义优化选项(可选):
options = optimoptions('lsqcurvefit', 'Display', 'iter');此处设置了优化选项,其中 `’Display’, ‘iter’` 表示在每次迭代中显示优化过程的详细信息。
5. 进行参数拟合:
x = lsqcurvefit(@myFunction, x0, xdata, ydata, lb, ub, options);这里使用 `lsqcurvefit` 函数进行参数拟合,传入参数拟合函数 `@myFunction`、初始猜测参数 `x0`、自变量数据 `xdata`、因变量数据 `ydata`,以及参数下界 `lb` 和上界 `ub`。`x` 将包含拟合后的参数值。
在这个例子中,你可以根据实际情况修改函数的形式、初始猜测参数、参数范围等,以适应你的数据和拟合需求。你也可以根据具体情况进一步控制优化选项,例如设置不同的显示模式、设置最大迭代次数等。
3、区别
`lsqcurvefit` 函数与之前提到的 `polyfit` 和 `polyval` 函数有以下几个主要区别:
1. 功能不同:`polyfit` 和 `polyval` 主要用于多项式拟合和求值,
适用于已知数据点遵循多项式模型
的情况。而 `lsqcurvefit` 用于非线性最小二乘曲线拟合,适用于更一般的非线性函数拟合问题。2. 参数个数:`polyfit` 和 `polyval` 方法中只涉及到多项式的阶数和系数,而 `lsqcurvefit` 方法需要提供更多的参数,包括拟合函数、初始猜测参数、数据点、参数界限等。
3. 拟合函数的选择:`polyfit` 和 `polyval` 只能用于多项式模型的拟合,而 `lsqcurvefit` 可以适应更广泛的非线性模型。你可以自定义拟合函数 `fun`,只要它能够接受待拟合参数和自变量作为输入,并返回拟合函数对应的因变量值。
4. 非线性优化:`lsqcurvefit` 使用非线性优化算法来拟合数据,它基于最小二乘法和迭代的思想,通过调整参数的值来改善拟合效果。相比之下,`polyfit` 使用最小二乘法来拟合多项式模型,但不涉及非线性优化过程。
总之,`lsqcurvefit` 提供了更灵活、更通用的拟合功能,适用于更广泛的曲线拟合问题,尤其在遇到非线性模型时更有优势。而对于已知数据点遵循多项式模型的情况,使用 `polyfit` 和 `polyval` 更为简便。
4、选择
选择使用 `polyfit`、`polyval` 还是 `lsqcurvefit` 取决于你的具体需求和数据特征。下面是一些建议来帮助你做出选择:
1. 数据特征:观察你的数据是否符合多项式模型。如果你的数据显示出明显的多项式关系,即使你不知道多项式的阶数,`polyfit` 和 `polyval` 可能是较好的选择,因为它们是最专门用于多项式拟合和求值的函数。
2. 拟合模型:确定你需要拟合的函数是否是一个多项式以外的非线性函数。如果你的函数不属于多项式模型,或者你需要对不同类型的非线性函数进行拟合,那么 `lsqcurvefit` 是更通用和灵活的选择,因为它允许你自定义拟合函数。
3. 参数估计:如果你已经确定你的函数是一个多项式模型,并且你希望直接估计多项式的系数,在不考虑其他模型的情况下,`polyfit` 可以提供简单且高效的多项式拟合。
4. 参数范围和约束:如果你对估计的参数有范围或约束条件,或者你面临的问题需要一种更灵活的非线性拟合方法,那么 `lsqcurvefit` 可能更适合你。它提供了对参数范围的设置,以及更高级的非线性优化算法,使得拟合过程更加灵活和精确。
综上所述,如果你的数据适用于多项式模型并且你想估计多项式的系数,可以选择 `polyfit` 和 `polyval`。如果你面临更一般的非线性函数拟合问题,或者需要参数范围和约束,那么 `lsqcurvefit` 是更适合的选择。