写在前面
1、本文内容
四元数、罗德里格斯公式、欧拉角、旋转矩阵推导和资料
2、转载请注明出处:
https://blog.csdn.net/qq_41102371/article/details/126002167
资料
四元数
Understanding Quaternions 中文翻译《理解四元数》 https://www.qiujiawei.com/understanding-quaternions/
http://mars.cs.umn.edu/tr/reports/Trawny05b.pdf
几种三维空间旋转的表达方式转换
三维旋转:欧拉角、四元数、旋转矩阵、轴角之间的转换 https://zhuanlan.zhihu.com/p/45404840
彻底搞懂“旋转矩阵/欧拉角/四元数”,让你体会三维旋转之美 https://blog.csdn.net/weixin_45590473/article/details/122884112
展示欧拉角与四元数动态变换关系的网站
https://quaternions.online/
罗德里格斯公式
https://en.wikipedia.org/wiki/Rodrigues’_rotation_formula
罗德里格斯公式(Rodrigues Formula) https://blog.csdn.net/weixin_40215443/article/details/123950141
二维xy坐标旋转 https://blog.csdn.net/qq_41102371/article/details/116245483#t4
推导
先放这,有空来推一遍
几种表达方式
K
K
K
是
k
k
k
的叉乘矩阵,即
K
=
k
∧
\mathbf{K}=\mathbf{k}^{\land}
K
=
k
∧
,(
k
\mathbf{k}
k
的叉乘矩阵也可表示为
k
×
\mathbf{k}_{\times}
k
×
)
1、
R
=
I
+
(
1
−
cos
θ
)
K
2
+
(
sin
θ
)
K
=
I
+
(
1
−
cos
θ
)
[
k
∧
]
2
+
(
sin
θ
)
k
∧
\begin{aligned} \mathbf{R}&=\mathbf{I}+(1-\cos\theta)\mathbf{K}^2+(\sin\theta)\mathbf{K}\\ &=\mathbf{I}+(1-\cos\theta)[\mathbf{k}^{\land}]^2+(\sin\theta)\mathbf{k}^{\land}\\ \end{aligned}
R
=
I
+
(
1
−
cos
θ
)
K
2
+
(
sin
θ
)
K
=
I
+
(
1
−
cos
θ
)
[
k
∧
]
2
+
(
sin
θ
)
k
∧
2、
由
K
2
=
k
∧
k
∧
=
k
k
T
−
I
\mathbf{K}^2=\mathbf{k}^{\land}\mathbf{k}^{\land}=\mathbf{k}\mathbf{k}^T-\mathbf{I}
K
2
=
k
∧
k
∧
=
k
k
T
−
I
可得
R
=
I
+
(
1
−
cos
θ
)
(
k
k
T
−
I
)
+
(
sin
θ
)
k
∧
=
cos
θ
I
+
(
1
−
cos
θ
)
k
k
T
+
(
sin
θ
)
k
∧
\begin{aligned} \mathbf{R}&=\mathbf{I}+(1-\cos\theta)(\mathbf{k}\mathbf{k}^T-\mathbf{I})+(\sin\theta)\mathbf{k}^{\land}\\ &=\cos\theta\mathbf{I}+(1-\cos\theta)\mathbf{k}\mathbf{k}^T+(\sin\theta)\mathbf{k}^{\land} \end{aligned}
R
=
I
+
(
1
−
cos
θ
)
(
k
k
T
−
I
)
+
(
sin
θ
)
k
∧
=
cos
θ
I
+
(
1
−
cos
θ
)
k
k
T
+
(
sin
θ
)
k
∧
3、
高博的14讲中推导了指数映射

R
=
e
x
p
(
θ
k
∧
)
=
cos
θ
I
+
(
1
−
cos
θ
)
k
k
T
+
(
sin
θ
)
k
∧
\mathbf{R}=exp(\theta \mathbf{k}^{\land})=\cos\theta\mathbf{I}+(1-\cos\theta)\mathbf{k}\mathbf{k}^T+(\sin\theta)\mathbf{k}^{\land}
R
=
e
x
p
(
θ
k
∧
)
=
cos
θ
I
+
(
1
−
cos
θ
)
k
k
T
+
(
sin
θ
)
k
∧
四元数转旋转矩阵
根据
http://mars.cs.umn.edu/tr/reports/Trawny05b.pdf
,四元数转旋转矩阵为:

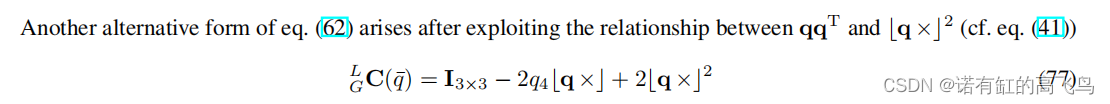
G
L
C
(
q
ˉ
)
=
(
2
q
4
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
q
q
T
=
(
2
q
4
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
+
2
∣
q
∣
2
⋅
I
3
×
3
=
(
2
q
4
2
+
2
∣
q
∣
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
=
(
2
q
4
2
+
2
(
q
1
2
+
q
2
2
+
q
3
2
)
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
=
(
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
=
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
\begin{aligned} {}_G^L\mathbf{C}(\bar{q})&=(2q_4^2-1)\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2\mathbf{q}\mathbf{q}^T\\ &=(2q_4^2-1)\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2[\mathbf{q}_{\times}]^2+2|\mathbf{q}|^2\cdot \mathbf{I}_{3\times3}\\ &=(2q_4^2+2|\mathbf{q}|^2-1)\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2[\mathbf{q}_{\times}]^2\\ &=(2q_4^2+2(q_1^2+q_2^2+q_3^2)-1)\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2[\mathbf{q}_{\times}]^2\\ &=(2-1)\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2[\mathbf{q}_{\times}]^2\\ &=\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2[\mathbf{q}_{\times}]^2 \end{aligned}
G
L
C
(
q
ˉ
)
=
(
2
q
4
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
q
q
T
=
(
2
q
4
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
+
2∣
q
∣
2
⋅
I
3
×
3
=
(
2
q
4
2
+
2∣
q
∣
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
=
(
2
q
4
2
+
2
(
q
1
2
+
q
2
2
+
q
3
2
)
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
=
(
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
=
I
3
×
3
−
2
q
4
[
q
×
]
+
2
[
q
×
]
2
其中
q
ˉ
=
[
q
q
4
]
=
[
q
1
,
q
2
,
q
3
,
q
4
]
T
\bar{q}=\begin{bmatrix}\mathbf{q}\\q_4\end{bmatrix}=[q_1,q_2,q_3,q_4]^T
q
ˉ
=
[
q
q
4
]
=
[
q
1
,
q
2
,
q
3
,
q
4
]
T
,
q
=
[
q
1
,
q
2
,
q
3
]
T
\mathbf{q}=[q_1,q_2,q_3]^T
q
=
[
q
1
,
q
2
,
q
3
]
T
,
q
1
2
+
q
2
2
+
q
3
2
+
q
4
2
=
1
q_1^2+q_2^2+q_3^2+q_4^2=1
q
1
2
+
q
2
2
+
q
3
2
+
q
4
2
=
1
则
G
L
R
=
[
1
−
2
q
2
2
−
2
q
3
2
2
(
q
1
q
2
+
q
3
q
4
)
2
(
q
1
q
3
−
q
2
q
4
)
2
(
q
1
q
2
−
q
3
q
4
)
1
−
2
q
1
2
−
2
q
3
2
2
(
q
2
q
3
+
q
1
q
4
)
2
(
q
1
q
3
+
q
2
q
4
)
2
(
q
2
q
3
−
q
1
q
4
)
1
−
2
q
1
2
−
2
q
2
2
]
{}_G^L\!R= \begin{bmatrix} 1-2q_2^2-2q_3^2& 2(q_1q_2+q_3q_4) & 2(q_1q_3-q_2q_4) \\ 2(q_1q_2-q_3q_4) & 1-2q_1^2-2q_3^2 & 2(q_2q_3+q_1q_4) \\ 2(q_1q_3+q_2q_4)& 2(q_2q_3-q_1q_4) & 1-2q_1^2-2q_2^2 \end{bmatrix}
G
L
R
=
⎣
⎡
1
−
2
q
2
2
−
2
q
3
2
2
(
q
1
q
2
−
q
3
q
4
)
2
(
q
1
q
3
+
q
2
q
4
)
2
(
q
1
q
2
+
q
3
q
4
)
1
−
2
q
1
2
−
2
q
3
2
2
(
q
2
q
3
−
q
1
q
4
)
2
(
q
1
q
3
−
q
2
q
4
)
2
(
q
2
q
3
+
q
1
q
4
)
1
−
2
q
1
2
−
2
q
2
2
⎦
⎤
即将世界坐标系下的点
P
G
P^G
P
G
旋转到局部坐标系下的点
P
L
P^L
P
L
P
L
=
G
L
R
P
G
P^L={}_G^L\!R P^G
P
L
=
G
L
R
P
G
而
三维旋转:欧拉角、四元数、旋转矩阵、轴角之间的转换 https://zhuanlan.zhihu.com/p/45404840
中是将局部坐标系下的点
P
L
P^L
P
L
转换到世界坐标系下的
P
G
P^G
P
G
:
L
G
R
=
[
1
−
2
q
2
2
−
2
q
3
2
2
(
q
1
q
2
−
q
3
q
4
)
2
(
q
1
q
3
+
q
2
q
4
)
2
(
q
1
q
2
+
q
3
q
4
)
1
−
2
q
1
2
−
2
q
3
2
2
(
q
2
q
3
−
q
1
q
4
)
2
(
q
1
q
3
−
q
2
q
4
)
2
(
q
2
q
3
+
q
1
q
4
)
1
−
2
q
1
2
−
2
q
2
2
]
{}_L^G\!R= \begin{bmatrix} 1-2q_2^2-2q_3^2& 2(q_1q_2-q_3q_4) & 2(q_1q_3+q_2q_4) \\ 2(q_1q_2+q_3q_4) & 1-2q_1^2-2q_3^2 & 2(q_2q_3-q_1q_4) \\ 2(q_1q_3-q_2q_4)& 2(q_2q_3+q_1q_4) & 1-2q_1^2-2q_2^2 \end{bmatrix}
L
G
R
=
⎣
⎡
1
−
2
q
2
2
−
2
q
3
2
2
(
q
1
q
2
+
q
3
q
4
)
2
(
q
1
q
3
−
q
2
q
4
)
2
(
q
1
q
2
−
q
3
q
4
)
1
−
2
q
1
2
−
2
q
3
2
2
(
q
2
q
3
+
q
1
q
4
)
2
(
q
1
q
3
+
q
2
q
4
)
2
(
q
2
q
3
−
q
1
q
4
)
1
−
2
q
1
2
−
2
q
2
2
⎦
⎤
P
G
=
L
G
R
P
L
P^G={}_L^G\!R P^L
P
G
=
L
G
R
P
L
这正好满足:
G
L
R
=
L
G
R
T
(
G
L
R
=
L
G
R
−
1
)
{}_G^L\!R ={
{}_L^G\!R}^T({}_G^L\!R ={
{}_L^G\!R}^{-1})
G
L
R
=
L
G
R
T
(
G
L
R
=
L
G
R
−
1
)
近似
根据
http://mars.cs.umn.edu/tr/reports/Trawny05b.pdf
原文当
δ
q
ˉ
\delta\bar{q}
δ
q
ˉ
非常小时

以下为个人理解的推导
G
L
C
(
q
ˉ
)
=
(
2
q
4
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
q
q
T
≈
(
2
×
1
2
−
1
)
I
3
×
3
−
2
×
1
[
1
2
δ
θ
×
]
+
2
×
0
3
×
3
=
I
3
×
3
−
[
δ
θ
×
]
\begin{aligned} {}_G^L\mathbf{C}(\bar{q})&=(2q_4^2-1)\mathbf{I}_{3\times3}-2q_4[\mathbf{q}_{\times}]+2qq^T\\ &\approx (2\times1^2-1)\mathbf{I}_{3\times3}-2\times 1[\frac{1}{2}\delta \mathbf{\theta}_{\times}]+2\times0_{3\times3}\\ &=\mathbf{I}_{3\times3}-[\delta \mathbf{\theta}_{\times}] \end{aligned}
G
L
C
(
q
ˉ
)
=
(
2
q
4
2
−
1
)
I
3
×
3
−
2
q
4
[
q
×
]
+
2
q
q
T
≈
(
2
×
1
2
−
1
)
I
3
×
3
−
2
×
1
[
2
1
δ
θ
×
]
+
2
×
0
3
×
3
=
I
3
×
3
−
[
δ
θ
×
]
其中
q
q
T
≈
0
3
×
3
qq^T\approx0_{3\times3}
q
q
T
≈
0
3
×
3
四元数与轴角
还是参考
http://mars.cs.umn.edu/tr/reports/Trawny05b.pdf
,
q
ˉ
=
[
q
q
4
]
=
[
q
1
q
2
q
3
q
4
]
=
[
k
x
sin
(
θ
/
2
)
k
y
sin
(
θ
/
2
)
k
z
sin
(
θ
/
2
)
cos
(
θ
/
2
)
]
=
[
k
^
sin
(
θ
/
2
)
cos
(
θ
/
2
)
]
,
k
^
=
[
k
x
,
k
y
,
k
z
]
T
,
q
4
=
cos
(
θ
/
2
)
\bar{q}=\begin{bmatrix}\mathbf{q}\\q_4\end{bmatrix}=\begin{bmatrix}q_1\\q_2\\q_3\\q_4\end{bmatrix}=\begin{bmatrix}k_x\sin(\theta/2)\\k_y\sin(\theta/2)\\k_z\sin(\theta/2)\\\cos(\theta/2)\end{bmatrix}=\begin{bmatrix}\hat{\mathbf{k}}\sin(\theta/2)\\\cos(\theta/2)\end{bmatrix},\hat{\mathbf{k}}=[k_x,k_y,k_z]^T,q_4=\cos(\theta/2)
q
ˉ
=
[
q
q
4
]
=
⎣
⎡
q
1
q
2
q
3
q
4
⎦
⎤
=
⎣
⎡
k
x
sin
(
θ
/2
)
k
y
sin
(
θ
/2
)
k
z
sin
(
θ
/2
)
cos
(
θ
/2
)
⎦
⎤
=
[
k
^
sin
(
θ
/2
)
cos
(
θ
/2
)
]
,
k
^
=
[
k
x
,
k
y
,
k
z
]
T
,
q
4
=
cos
(
θ
/2
)
转换代码
欧拉角转旋转矩阵
#include <Eigen/Core>
#include <Eigen/Dense>
#include <iostream>
#define PI 3.1415926
int main(int argc, char* argv[]){
std::cout<<PI<<std::endl;
if(argc<4){
std::cout<<"please input a 3x1 vector,for example:\neuler2rt 45 30 60"<<std::endl;
return 0;
}
Eigen::Vector3d eulerAngle(atof(argv[1]),atof(argv[2]),atof(argv[3]));
std::cout<<"eulerAngle:\nx: "<<eulerAngle[0]<<" y: "<<eulerAngle[1]<<" z: "<<eulerAngle[2]<<std::endl;
eulerAngle=eulerAngle/180*PI;
Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
Eigen::AngleAxisd rollAngle(Eigen::AngleAxisd(eulerAngle[0],Eigen::Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(Eigen::AngleAxisd(eulerAngle[1],Eigen::Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(Eigen::AngleAxisd(eulerAngle[2],Eigen::Vector3d::UnitZ()));
rotation_matrix=rollAngle*pitchAngle*yawAngle;
std::cout<<"rotation_matrix:\n"<<rotation_matrix<<std::endl;
Eigen::Vector3d eulerAngle2=rotation_matrix.eulerAngles(0,1,2);
std::cout<<"eulerAngle:\nx: "<<eulerAngle2[0]/PI*180<<" y: "<<eulerAngle2[1]/PI*180<<" z: "<<eulerAngle2[2]/PI*180<<std::endl;
return 0;
}
使用
erluer2rt 30 45 60
旋转矩阵转欧拉角和四元数
#include <Eigen/Core>
#include <Eigen/Dense>
#include <iostream>
#include <fstream>
#define PI 3.1415926
int main(int argc, char* argv[]){
if(argc<2){
std::cout<<"please input a file including a 3x3 matrix"<<std::endl;
return 0;
}
std::string filename;
filename=argv[1];
std::ifstream fin;
fin.open(filename,std::ios::in);
if(!fin.is_open()){
std::cout<<"read file "<<filename<<" failed."<<std::endl;
return 0;
}
Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
for (std::size_t i = 0; i < 3; ++i) {
for (std::size_t j = 0; j < 3; ++j) {
double value;
fin >> value;
// std::cout<<value<<" ";
rotation_matrix(i, j) = value;
}
}
std::cout<<std::endl;
fin.close();
std::cout<<"rotation_matrix:\n"<<rotation_matrix<<std::endl;
Eigen::Vector3d eulerAngle=rotation_matrix.eulerAngles(0,1,2);
// std::cout<<eulerAngle<<std::endl;
std::cout<<"eulerAngle:\nx: "<<eulerAngle[0]/PI*180<<" y: "<<eulerAngle[1]/PI*180<<" z: "<<eulerAngle[2]/PI*180<<std::endl;
//转四元数
Eigen::Quaterniond rotation_q(rotation_matrix);
std::cout<<"rotation_q:\nx: "<<rotation_q.x()<<" y:"<<rotation_q.y()<<" z:"<<rotation_q.z()<<" w:"<<rotation_q.w()<<" "<<std::endl;
return 0;
}
使用
rt2euler r_3x3.txt
其中r_3x3.txt格式如下
1 0 0
0 1 0
0 0 1
参考
使用Eigen实现四元数、欧拉角、旋转矩阵、旋转向量之间的转换
http://t.zoukankan.com/long5683-p-14373627.html
完
如有错漏,敬请指正
——————————————————————————————–202207