博客

《机器人学导论》约翰 第二章

  • Post author:
  • Post category:其他



目录


第2章 空间描述和变换


2.1 引言


2.2 描述：位置 姿态 位姿


2.3 映射：从一个坐标系到另一个坐标系的变换


2.4 算子：平移，旋转和变换


2.5 总结和说明


2.6变换的计算


2.7变换方程


2.8其他姿态描述


2.9 自由矢量的变换


2.10计算问题

第2章 空间描述和变换

2.1 引言


机器人操作：

通过某种机构使零件和工具在空间运动，而为了表达运动就必须要引入一个

世界坐标系

2.2 描述：位置 姿态 位姿



1.位置：


如图表示在坐标系里点p的位置




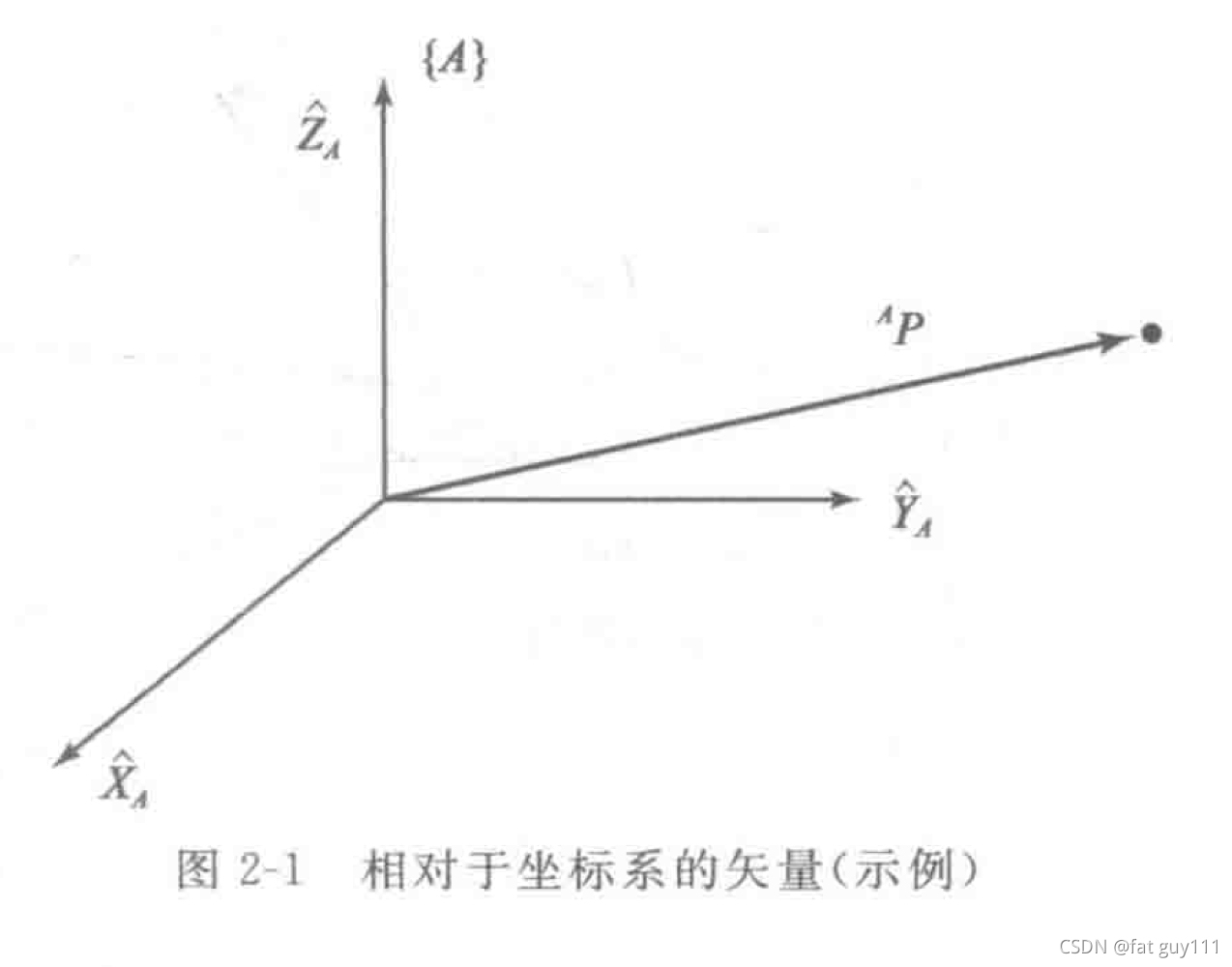
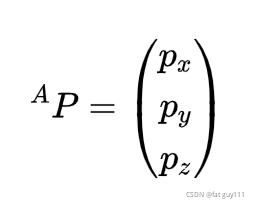
2.姿态：



旋转矩阵的表示

_{}^{A}\textrm{}X_{B}
表示坐标系B主轴方向的单位向量相对于A坐标系的矢量


R是旋转矩阵，它表示{B}对于｛A｝的表达


记忆上述矩阵的技巧：第一行都有XA 第一列都有XB


即矩阵的行是｛A｝的单位矢量在｛B｝中的表达


重点：

1.绕x轴旋转
\theta
角的矩阵

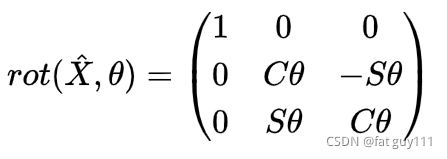
2.绕y轴旋转
\theta
角的矩阵

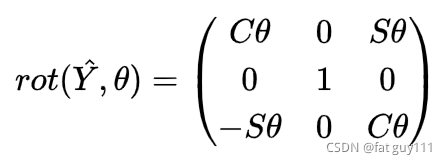
3. 绕z轴旋转
\theta
角的矩阵



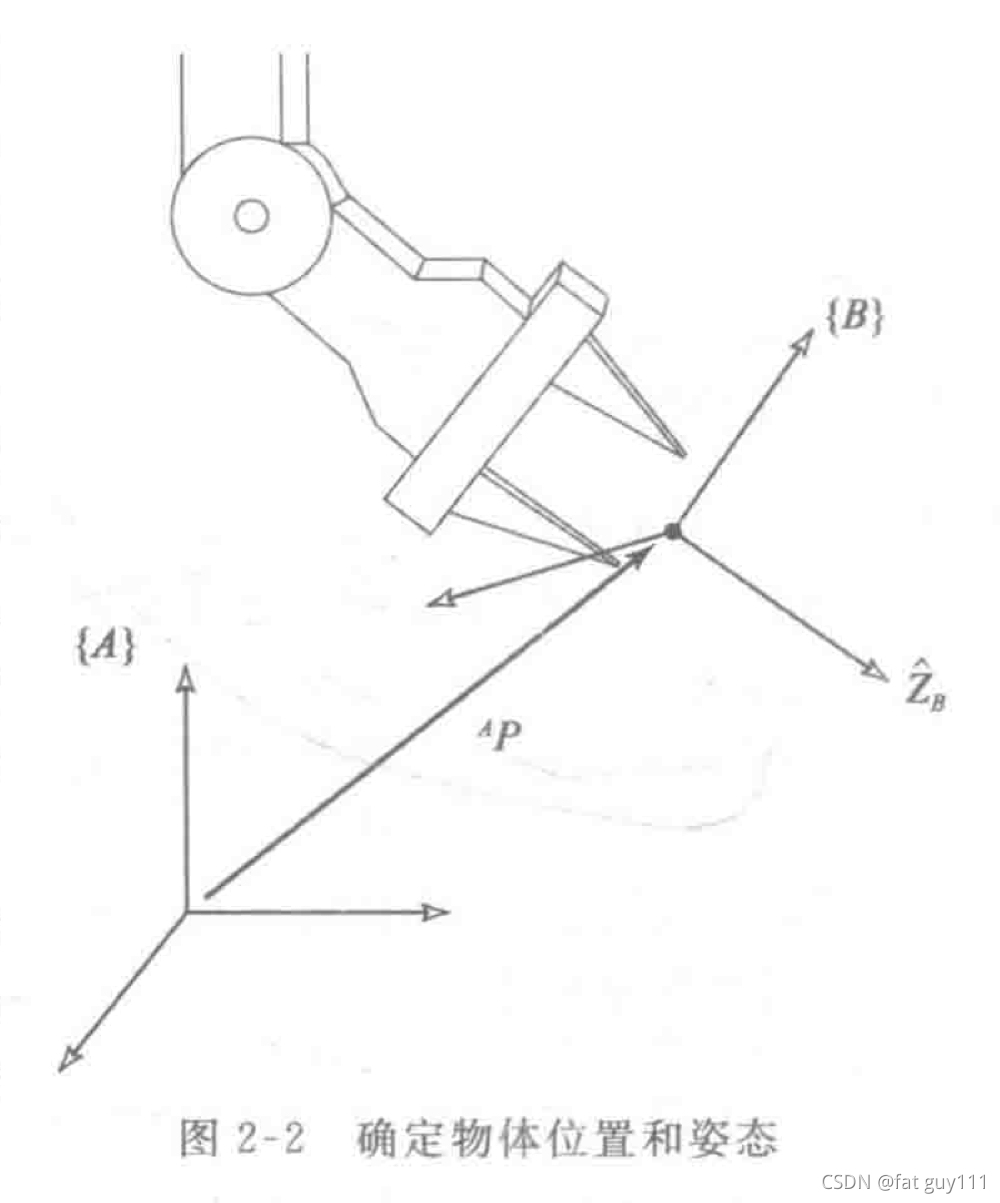
3.位姿：




位置和姿态的组合描述

其中前者是旋转矩阵，后者是确定位姿｛B｝的原点相对于{A}的位置

2.3 映射：从一个坐标系到另一个坐标系的变换



_{}^{A}\textrm{P}
表示点P相对于A坐标系原点的位置矢量

接下来的问题就是由已知的
_{}^{B}\textrm{P}
求
_{}^{A}\textrm{P}


1.坐标平移


2.坐标旋转


3.一般变换

坐标变换的结果如下


其中
^{A}P_{BORG}
表示B坐标系的坐标原点相对于A坐标系原点的位置矢量

引入一个新的概念形式

上述形式用矩阵算子（齐次变换矩阵）可表示为

2.4 算子：平移，旋转和变换


1.平移算子

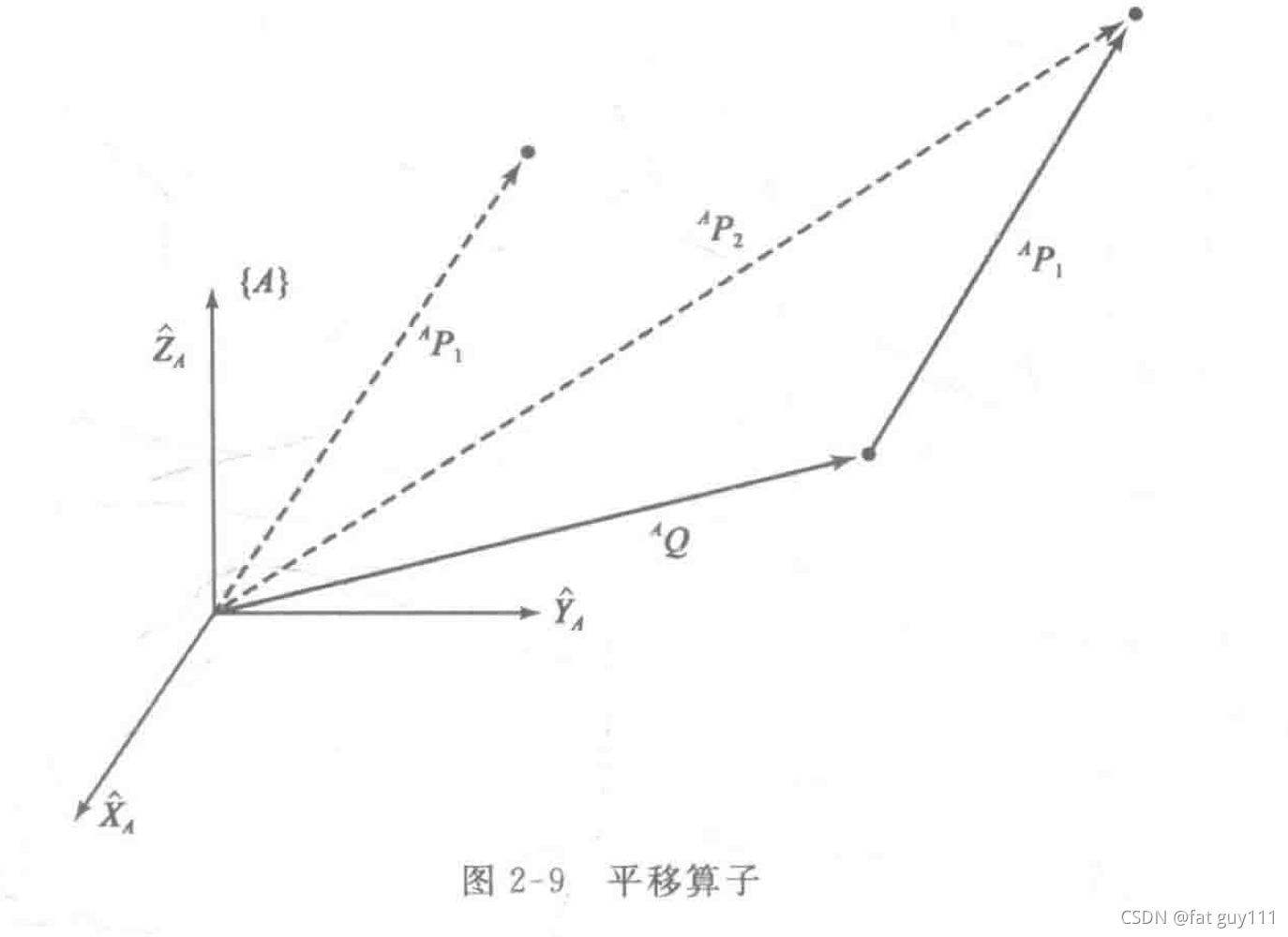
如图：
_{}^{A}\textrm{}P_{2}=_{}^{A}\textrm{}P_{1}+_{}^{A}\textrm{}Q

用矩阵算子写出平移变换，有：
_{}^{A}\textrm{}P_{2}=D_{Q}(q)_{}^{A}\textrm{}P_{1}

其中，q是沿着矢量Q平移的数量，有符号，算子
_{}^{}\textrm{}D_{Q}
可被看作一个特殊形式的齐次变换。

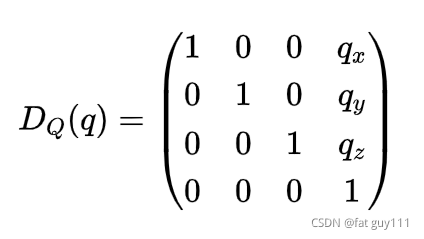
其中
q_{x}
,
q_{y}
和
q_{z}
是平移矢量Q的分量，并且有
q=(q_{x}^{2}+q_{y}^{2}+q_{z}^{2})^{1/2}


2.旋转算子

旋转算子的一般形式为
_{}^{A}\textrm{}P_{2}=R_{}^{A}\textrm{}P_{1}

用另一个符号定义旋转算子以明确的说明是绕哪个轴旋转的:
_{}^{A}\textrm{}P_{2}=R_{K}(\theta )_{}^{A}\textrm{}P_{1}

R_{K}(\theta )
表示绕K轴旋转
\theta
角的旋转算子，以绕Z轴旋转的算子为例：

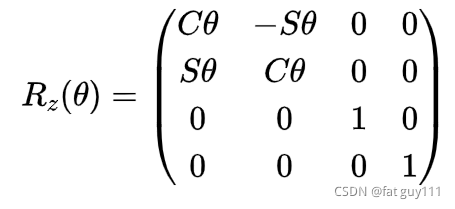
其中位置矢量的分量为0


3.变换算子

与矢量和旋转矩阵一样，坐标系还可以用变换算子来定义，算子T既包含了平移Q也包含了平移


^{A}P_{2}=T^{A}P_{1}

2.5 总结和说明

2.6变换的计算


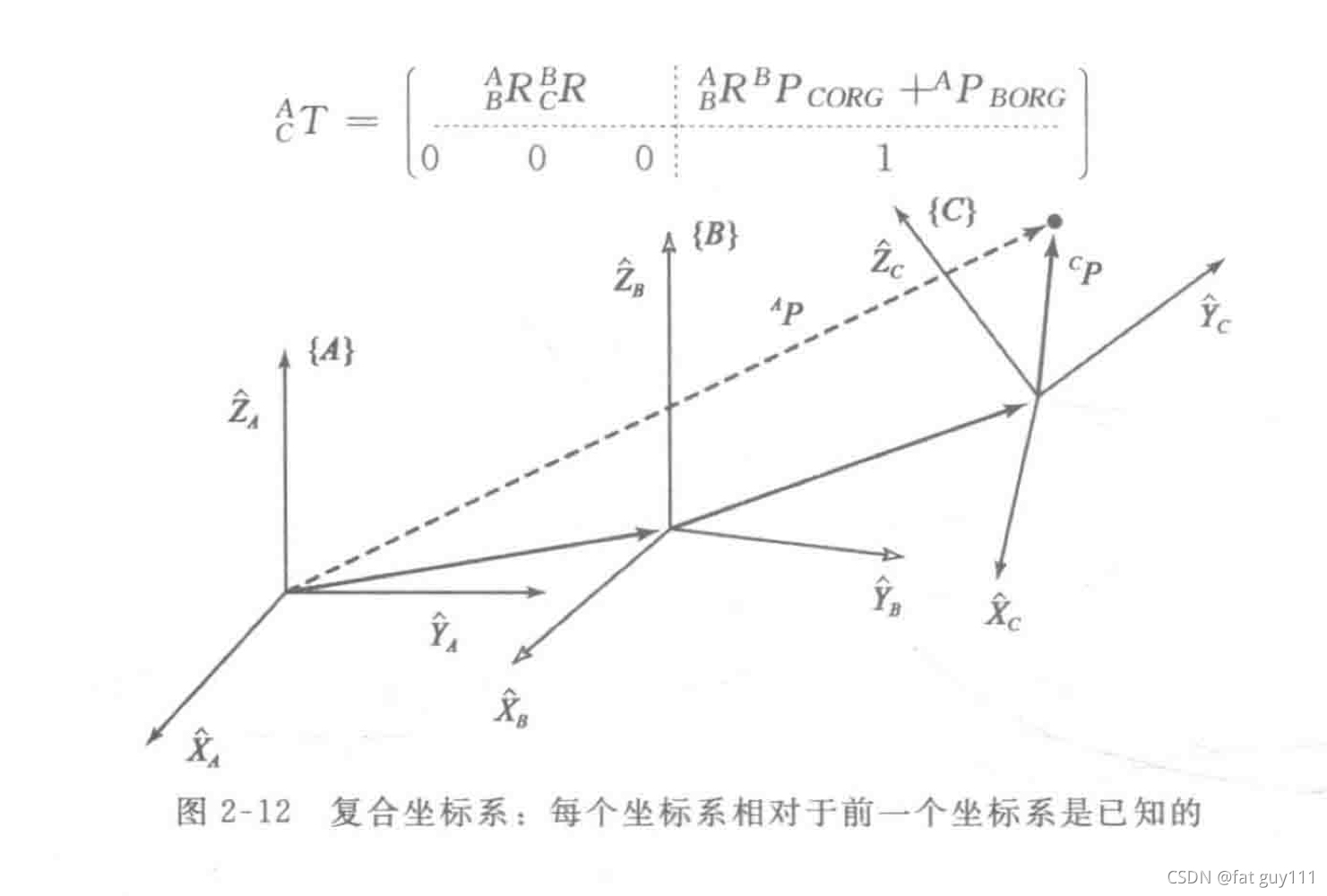
1.复合变换

已知坐标系｛C｝相对于坐标系｛B},{B}相对于｛A}

由此定义
_{C}^{A}T=_{B}^{A}T_{C}^{B}T

即：


2.逆变换


已知
_{B}^{A}T
,求
_{A}^{B}T


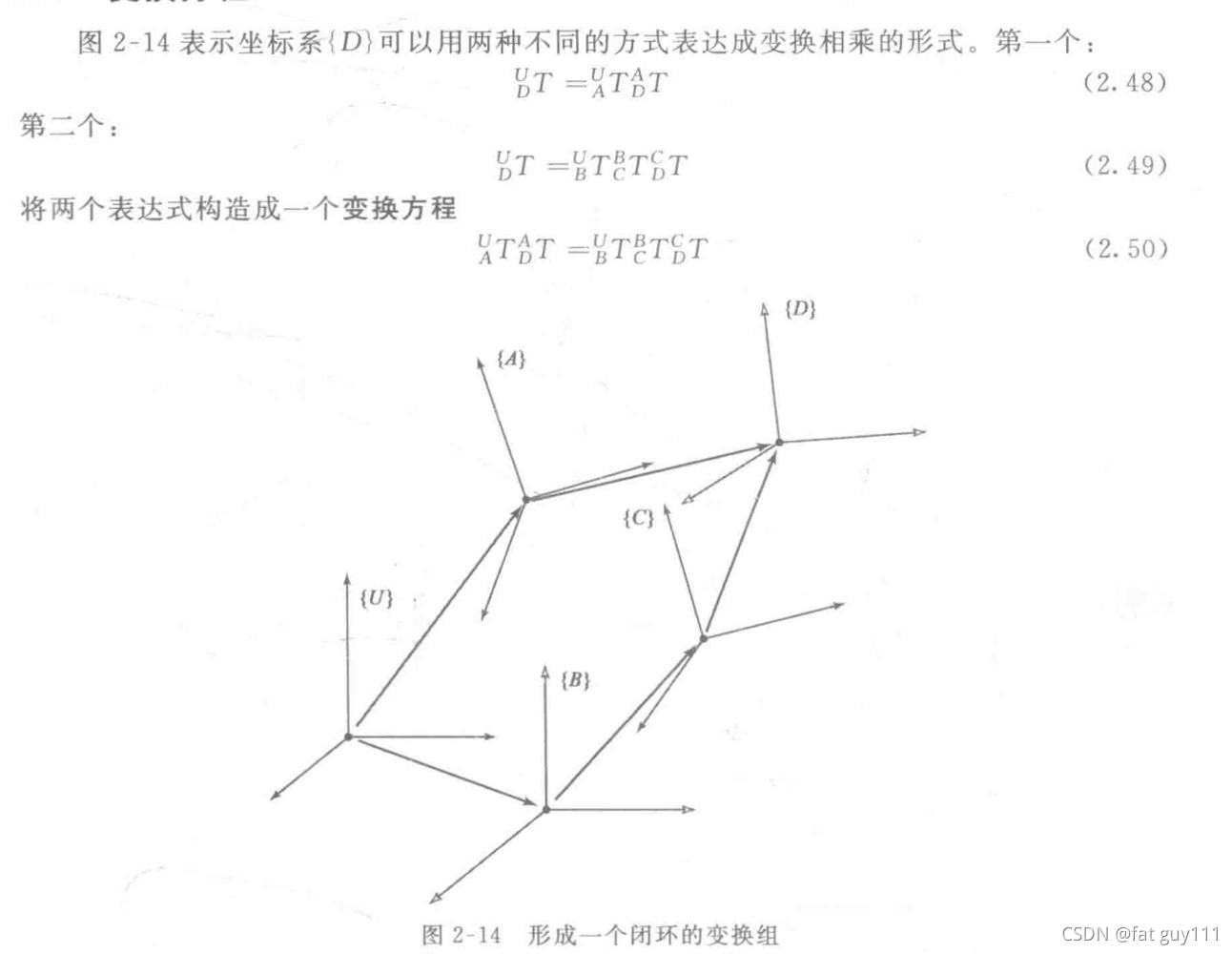
2.7变换方程

坐标系的图形表示法：用箭头的方向指明坐标系定义的方式

2.8其他姿态描述

至此，只给出了用3*3旋转矩阵来表示姿态。如上所述，旋转矩阵是一种特殊的各列相互正交的单位阵。其行列式恒为+1，旋转矩阵也可被称作

标准正交阵。

显然，旋转矩阵的9个分量并不是完全独立的，这9个元素一定有如下6个约束。

首先，假定R为3列即
R=(\hat{X} \hat{Y} \hat{Z})
,那么：


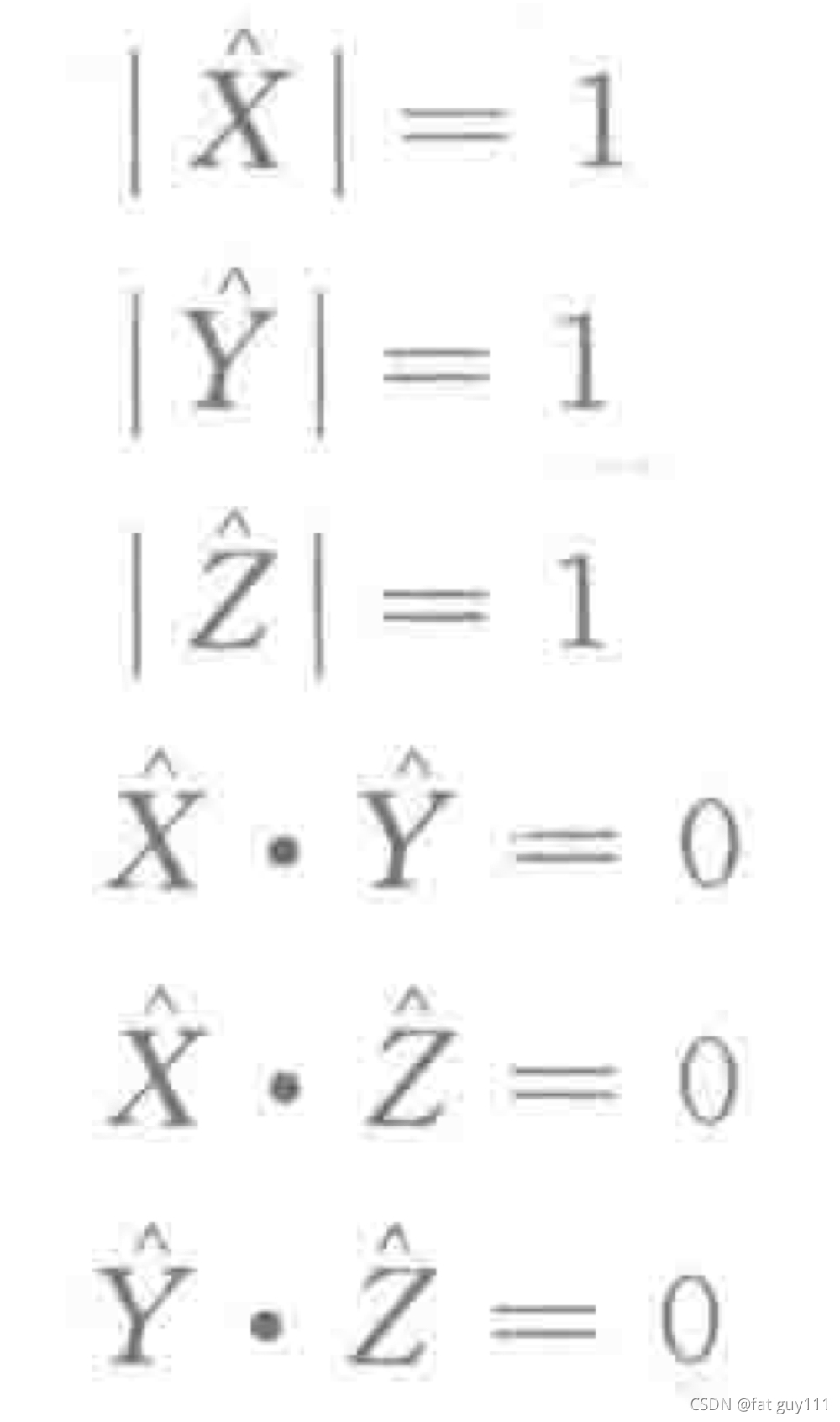
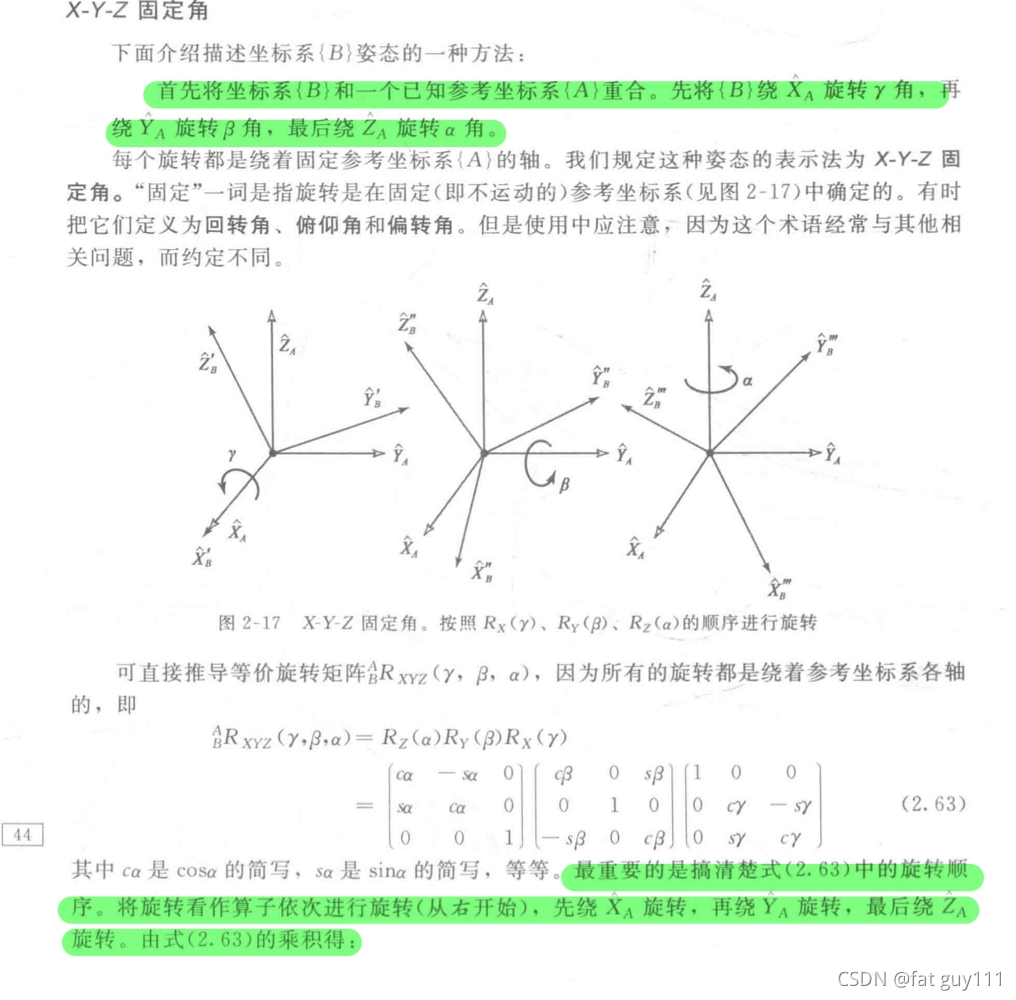
X—Y—Z固定角

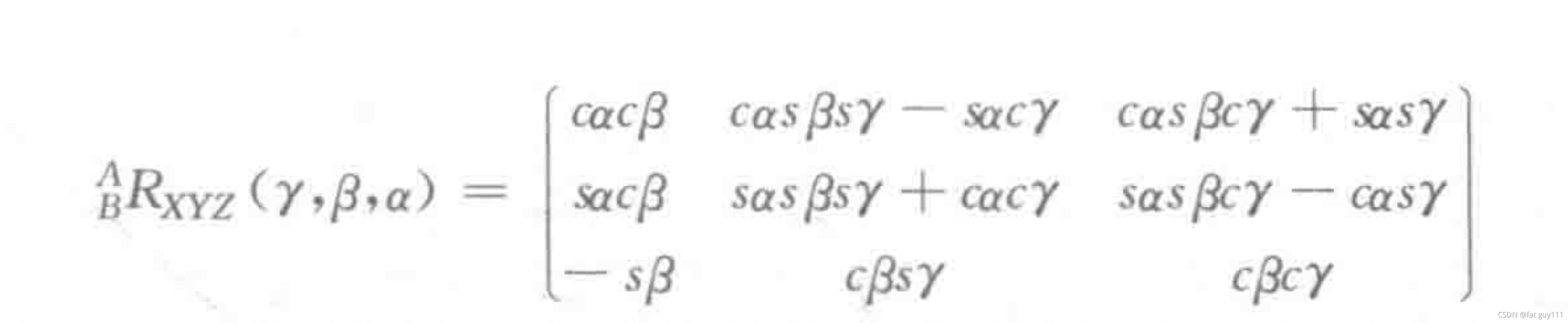
其他的描述方法（如Z——Y——X欧拉角等）大同小异都是用3个角度变量来描述旋转坐标系）

2.9 自由矢量的变换


矢量相等

：具有相同的维数，大小和方向


矢量等效

：在某一功能上产生了相同的作用效果


线矢量

：与作用线有关的矢量


自由矢量

：可能出现在空间任意位置的矢量

2.10计算问题


版权声明：本文为stay__hungry_y原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。