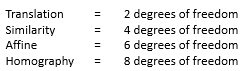图像几何变换知识总结
图像变换知识总结
1.相似变换(Similarity transformations)
相似变换是平移、旋转和缩放的集合,那么相似变换后图片中的垂直和平行关系不会改变,比如变换前平行的特征变换后依然保持平行。

包括:

平移

平移+旋转
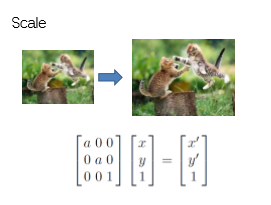
缩放
2.仿射变换(Affine transformations)
如果一幅图像中的直线经过映射到另一幅图下那个仍为直线,且保持平行关系,则为仿射变换(包括平移,旋转,缩放,反转etc)

(a1-a4 为旋转、缩放;tx、ty为平移)

包括:

平移

平移+旋转
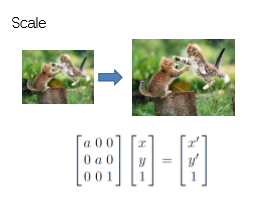
缩放

长宽比调整

剪切
3.单应性变换(Homogeneous Transformation)/ 透视变换(Perspective Transformation)
单应性:一个Homography是一个变换(3×3矩阵),将一个图像中的点映射到另一个图像中的对应点。单应性变换其实就是一个平面到另一个平面的变换关系。 透视:如果一幅图像中的直线经过映射到另一幅图下那个仍为直线,但是有些直线间可以没有保持平行关系,则为透视变换。主要的区别还是我们变换的图片中的物体是二维的还是三维的。(二者表面理解其实没区别,参考链接:https://blog.csdn.net/qq_40891636/article/details/106917776)
4.单应性矩阵求法

=>
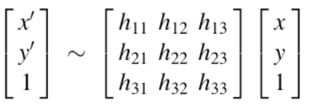
=>(八点法求解H矩阵:)

5.基础矩阵求法
在对极几何中,八点法求解F矩阵:同理
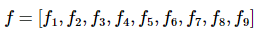
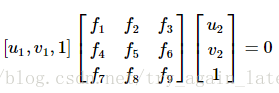
=>
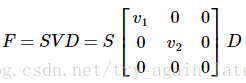
注: