目录
1.插入排序
● 具体思路
① 首先,第一个元素默认有序,保存下标为1的元素(1~arr.length – 1是待排序元素)。
② 依次取出待排序元素,在有序区间找待排序元素可以插入的位置插入待排序元素。
③ 每次有序区间的元素个数+1,而待排序区间的元素个数-1。
注:默认都以升序排序。
● 排序过程演示
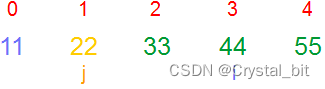
1) 第一个元素,默认有序,有序区间为[0, j ],待排序区间为[ i ,arr.length – 1]。



2) 在有序区间中找到当前待排序元素arr[i] 可以插入的位置(
有序区间中从后往前第一个比temp值小的元素下标位置
),如果找到了则结束内循环并将保存的temp( arr[i] )值,赋值到对应有序区间的下标(j + 1)处,没有找到则继续往前遍历,且将有序区间的元素依次往后挪动,直到找到待排序元素可以插入的位置,如果在有序区间中没有找到,那么说明当前待排序元素temp为有序区间第一个一个元素(
比有序区间的所有值都要小
)。
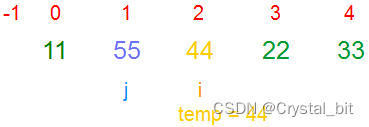
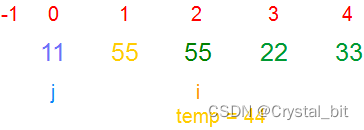
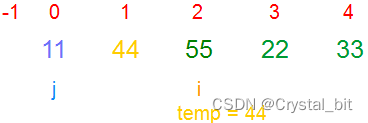
注:arr[j] < temp 结束内循环,j + 1位置就是temp插入的位置arr[j + 1]
3) 重复2)步骤,有序区间为[0,2],待排序区间为[3,arr.length – 1]。
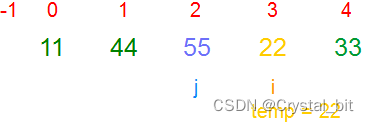

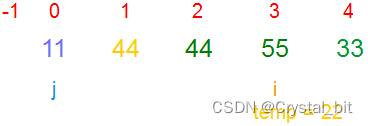
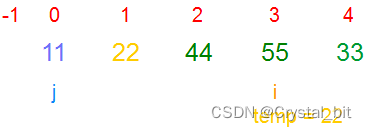
4) 重复2)步骤,有序区间为[0,3],待排序区间为[4,arr.length – 1]。
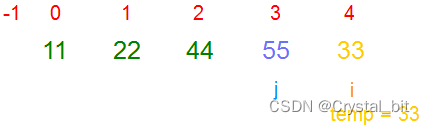
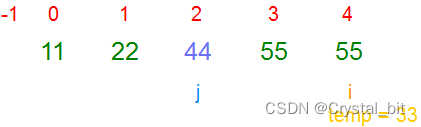
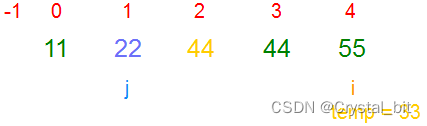
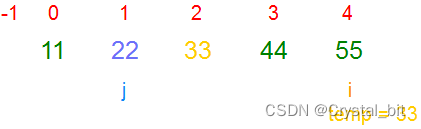
排序完毕,有序区间[0,arr.length – 1],待排序数组已经有序。
● 实现代码
/**
* 插入排序
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:稳定
* @param arr 待排序数组
*/
public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int temp = arr[i];
int j;
for (j = i - 1; j >= 0 ; j--) {
if(arr[j] > temp) {
arr[j + 1] = arr[j];
}else break;
}
arr[j + 1] = temp;
}
}
2.希尔排序
是插入排序的优化,在排序过程中待排序数组根据gap增量进行插入排序,使子区间有序从而使整个待排序数组越来越有序。
● 具体思路
① 设置gap增量,这里gap的初始值为待排序数组的元素个数 / 2,每次以2倍的数量减少。
② 原本的插入排序间隔是1,这里我们是gap,用gap进行分组排序。
③ gap越大,每组的元素个数就越少,反之,每组的元素个数越多。直到gap减少到1,则相当于让待排序数组进行直接插入排序。
注:希尔排序避免了当待排序数组为逆序时,直接插入排序达到最坏时间复杂度O(N^2)的情况,希尔排序是先根据gap增量对 待排序数组 进行预排序,最基本排序思路还是
依次取出[gap,arr.length – 1]位置的元素在对应组内的有序区间中找到插入位置插入
,所以说
希尔排序是插入排序的优化。
● 排序过程演示
1) 根据gap进行分组,组间进行插入排序。gap = arr.length / 2 = 2。
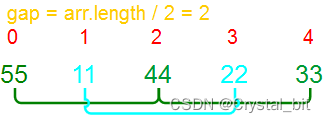
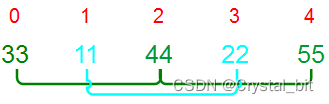
2) gap /= 1。
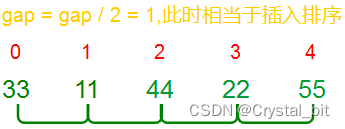

注:希尔排序中i = gap(每一趟++,直到等于arr.length – 1),j = i – gap(查找待排序元素的插入位置时,j = j – gap,按组进行查找)。最外层gap不断 / 2直到等于1,则相当于插入排序。
● 实现代码
/**
* 希尔排序
* 时间复杂度:O(N^1.3)
* 空间复杂度:O(1)
* 稳定性:不稳定
* @param arr 待排序数组
*/
public static void shellSort(int[] arr) {
int gap = arr.length / 2;
while(gap >= 1) {
for (int i = gap; i < arr.length; i++) {
int temp = arr[i];
int j ;
for (j = i - gap; j >= 0; j-=gap) {
if(arr[j] > temp) {
arr[j + gap] = arr[j];
}else break;
}
arr[j + gap] = temp;
}
gap/=2;
}
}
3.选择排序
● 具体思路
① 默认第一个元素为最小,从之后的区间进行遍历找到最小值,与第一个元素进行交换
② 依次从待排序区间中找出最小的元素和有序区间(从0开始)的最后一个元素交换
③ 第一次取出最小的元素放最前面,第二次取出次小的放最小元素的后面…..直到只剩一个元素。排序完毕。
● 排序过程演示
1) 假设当前最小值的下标为minIndex,从minIndex之后的区间找到比其默认最小值更小的元素下标,不断更新minIndex,直到遍历完minIndex之后的区间。将minIndex位置的元素与最初minIndex位置( i )的元素相交换。
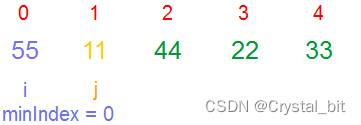
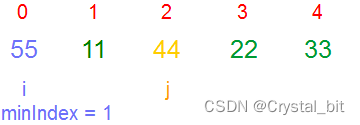
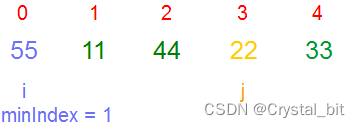
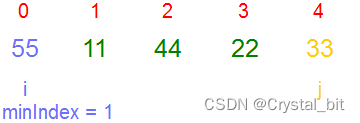


2)第二趟,确定的minIndex为3,与 i ( 1 ) 位置的元素交换。


3)第三趟,确定的minIndex为4,与 i ( 2 ) 位置的元素交换。
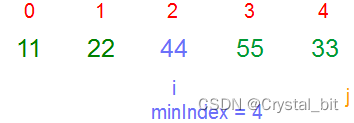

4)第四趟,确定的minIndex为4,与 i ( 3 ) 位置的元素交换。
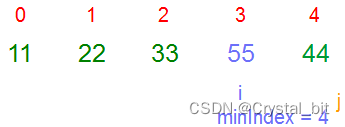
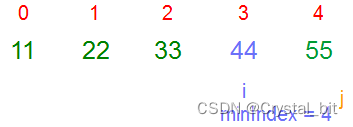
此时待排序数组已然有序。
● 实现代码
/**
* 选择排序
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:不稳定
* @param arr 待排序数组
*/
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if(arr[j] < arr[minIndex]) {
minIndex = j;
}
}
swap(arr,i,minIndex);
}
}
/**
* 选择排序第二种实现方式
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:不稳定
* @param arr 待排序数组
*/
public static void selectSort2(int[] arr) {
int left = 0,right = arr.length - 1;
while(left < right) {
int minIndex = left;
int maxIndex = left;
for (int i = left + 1; i <= right; i++) {
if(arr[i] > arr[maxIndex]) maxIndex = i;
if(arr[i] < arr[minIndex]) minIndex = i;
}
swap(arr,left,minIndex);
if(maxIndex == left) maxIndex = minIndex;
swap(arr,right,maxIndex);
left++;
right--;
}
}
4.冒泡排序
● 具体思路
① 最外层循环决定要排序的趟数
② 每趟的相邻元素之间进行比较后交换位置,确定一个最大值。
③ 直到待排序区间元素个数为1,则无需再进行冒泡排序
注:其优化是针对 待排序数组有序或接近有序的情况,设置一个flag判断当前趟中是否进行了元素交换,没有进行元素交换,则说明待排序数组已然有序。
● 排序过程演示
1) 第一趟(i = 0),j从0开始,不断与相邻元素进行比较,将最大值交换到最后面。

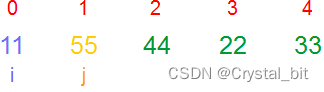
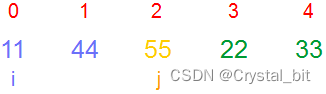
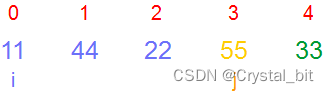

2) 第二趟(i = 1决定趟数),j (j < arr.length – 1 – i)从0开始,不断与相邻元素进行比较,将次大值交换到倒数第二个位置。
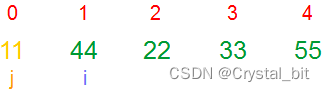


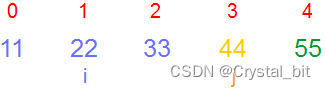
3) 第三趟(i = 2决定趟数),j (j < arr.length – 1 – i)从0开始,不断与相邻元素进行比较,确定第三个较大值。
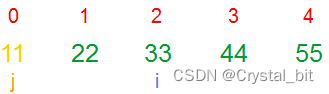
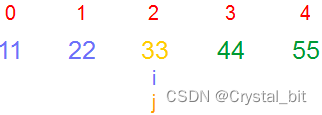
4) 第四趟(i = 3决定趟数),j (j < arr.length – 1 – i)从0开始,不断与相邻元素进行比较,确定第四个较大值。
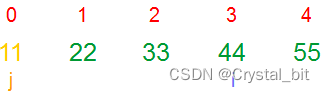
注:排序五个位置中四个位置已经确定,剩下一个元素也能直接确定,无需再进行排序。所以在待排序数组整体都是逆序时,冒泡排序的趟数为arr.length – 1,如果待排序数组在某一趟冒泡排序完成后就已经有序,则根据flag在第几趟为false时,才能确定冒泡排序的趟数。
● 实现代码
/**
* 冒泡排序
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:稳定
* @param arr 待排序数组
*/
public static void bubbleSort(int[] arr) {
boolean flag = false;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if(arr[j] > arr[j+1]) {
swap(arr,j,j+1);
flag = true;
}
}
if(!flag) {
return;
}
}
}
5.堆排序
● 具体思路
①将待排序数组元素构建成一个大堆,然后与优先级队列中的删除操作类似,取出堆顶最大元素和最后一个元素交换。
② 向下调整重新恢复成大堆,再取堆顶最大元素放倒数第二个位置。
③ 重复上诉操作。每次待排序区间元素个数-1,有序区间元素个数+1,直到待排序区间中只剩下一个元素。
● 排序过程演示
1) 将(55,11,44,22,33)序列构建成大堆(可以用向上调整也可以用
向下调整(优先推荐)
,具体过程可以看我这篇博客:
优先级队列(堆)详解
)。
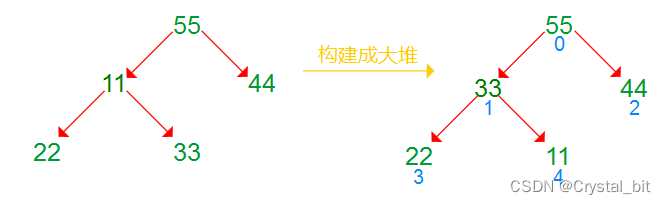
2) 取出堆顶元素与最后一个元素交换,重新向下调整恢复成大堆。
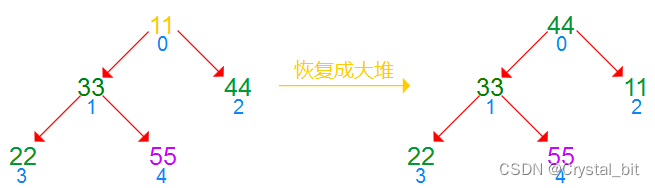
3) 重复步骤2),直到绿色待排序区间只剩下一个元素。
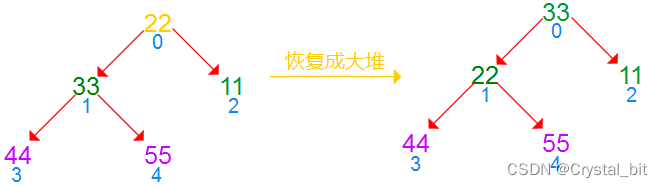
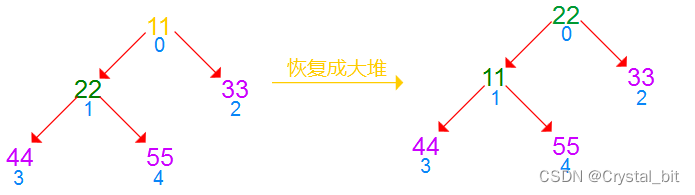
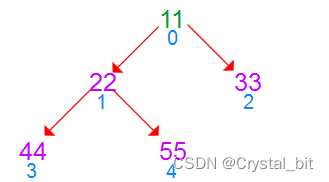
此时待排序区间只剩下一个元素,则完成排序。
● 实现代码
/**
* 堆排序
* 时间复杂度:O(N*logN(以2为底))
* 空间复杂度:O(1)
* 稳定性:不稳定
* @param arr 待排序数组
*/
public static void heapSort(int[] arr) {
//建大堆
createHeap(arr);
int maxSize = arr.length - 1;
while(maxSize > 0) {
swap(arr,0,maxSize);
adjustDown(arr,0,maxSize);
maxSize--;
}
}
/**
* 向下调整建堆
* 时间复杂度:O(N)
* 空间复杂度:O(1)
* @param arr 待建堆数组
*/
private static void createHeap(int[] arr) {
for (int i = (arr.length - 1 - 1) / 2; i >= 0; i--) {
//向下调整
adjustDown(arr,i,arr.length);
}
}
/**
* 向下调整
* @param arr 待调整数组
* @param parent 父亲结点下标
* @param length 向下调整终止条件
*/
private static void adjustDown(int[] arr, int parent, int length) {
int child = 2*parent + 1;
while(child < length) {
if(child + 1 < length && arr[child] < arr[child + 1]) {
child++;
}
if(arr[child] > arr[parent]) {
swap(arr,child,parent);
parent = child;
child = 2*parent + 1;
}else break;
}
}
6.快速排序
● 具体思路
1) 挖坑法
① 默认取第一元素作为基准值,先右边找小,填坑,然后左边找大,填坑。直到左边下标大于等于右边下标。
② 最后将基准值放入最后一个坑的位置,返回基准值下标。
③ 让基准值的左边和右边的无序区间再次进行①,②步,直到最左边和最右边相遇或错过
2) hoare法
① 默认取第一元素作为基准值,先右边找小,左边找大,停下来交换左右下标的元素值。直到左边下标大于等于右边下标。
② 最后将基准值与左右下标相遇的位置的元素交换,返回基准值下标。
③ 让基准值的左边和右边的无序区间再次进行①,②步,直到最左边和最右边相遇或错过
3) 前后指针法
① 第一个元素默认有序,保存下标为1的元素(1~arr.length – 1是待排序元素)。
② 依次取出待排序元素,在有序区间找待排序元素可以插入的位置。
③ 每次有序区间的元素个数+1,而待排序区间的元素个数-1。
● 排序过程演示
1) 挖坑法
① 默认第一个元素为基准值,保存基准值,在右边找小填到左边的坑位置。直到left >= right。结束查找,将保存的pilot值填入到最后一个坑位置。






② 因为待排序数组中第一个元素55为数组中最大值,且作为基准值,所以它的右边没有区间,没有一个元素比它大,且其它元素都比它小,都在它的左边。此时待排序数组还未完全有序,我们需要对基准值位置的左右(当前待排序数组中55为最大,没有右区间,left 会大于right)两边区间再次进行递归快速排序,直到left >= right 才结束快速排序。




③基准值33的 左区间[0,pilotIndex – 1] ,右区间[pilotIndex + 1,3] (55的位置已经确定),重复步骤②,直到每个基准值的左右区间都确定。
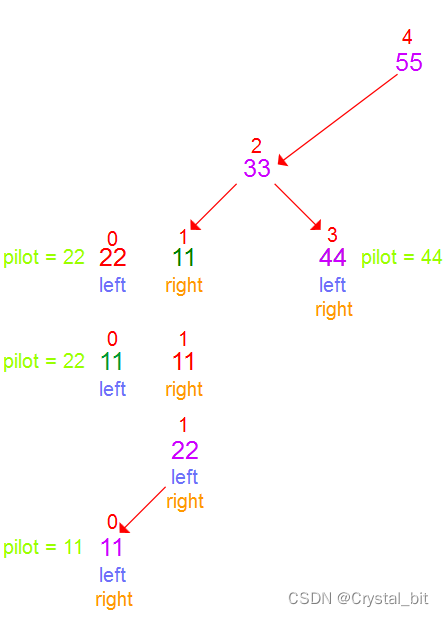
直到紫色部分连起来有序,那么整个待排序区间则有序。
2) hoare法(
整体快速排序的递归方式一致,不同的是找基准值位置的方式不同
)
① 默认第一个元素为基准值,保存基准值,在右边找小左边找大,找到交换左右两边的值,继续查找交换直到left >= right ,最后交换left和最初保存的基准值的位置。



② 55的左区间再次进行快排,重复步骤①。
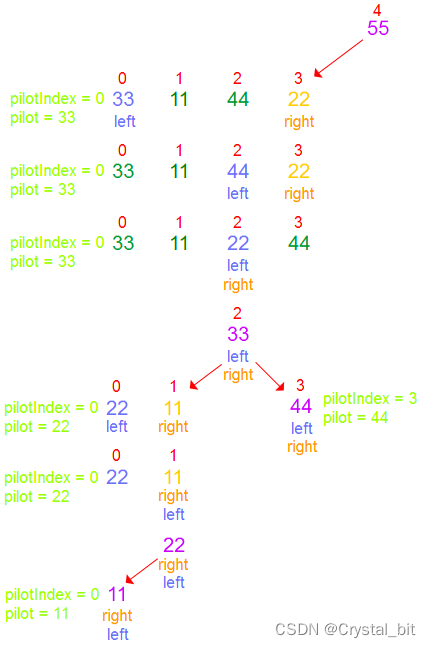
注:挖坑法和hoare法都要保证先右后左,否则会导致基准值大的元素会在基准值的前面。
3) 前后指针法(
整体快速排序的递归方式一致,不同的是找基准值位置的方式不同
)
① 默认第一个元素为基准值,保存基准值,后指针不断从后找比基准值小的与前指针交换。前指针开始指向后指针指向的前一个元素,当后指针找到比基准值小的元素后,如果前指针的后一个位置的元素不为后指针指向的元素的话,则后指针指向位置与前指针的后一个位置的元素相交换,相反则后指针继续往后移动。直到后指针>right,那么最后pre指向的元素与基准下标(left)的元素进行交换。

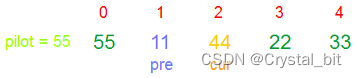




② 重复步骤①,继续对基准值的左右区间进行快速排序。
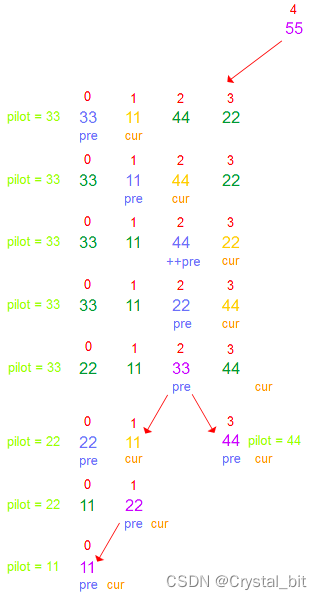
注:左边区间的left = 传入的left,right = pilotIndex – 1,而右边区间的left = pilotIndex + 1, right = 传入的right。
● 快速排序的优化
当待排序数组默认升序或降序时,进行快速排序,就会出现快速排序的最坏情况,根据基准划分的左右区间极度不均匀(只有左区间或只有右区间)。就像过程展示中基准值55为待排序数组中最大值,而它没有右区间,如果选取的基准值为待排序数组中最小值则没有左区间。会导致快速排序效率降低。
1) 选取恰当的基准值
● 随机取基准法
默认随机从待排序区间选取一个基准值。(不推荐,运气成分比较高)
● 三数取中法
从待排序区间中取三个数,分别是其第一个元素,中间元素,最后一个元素,进行比较,将它们三个数的中间数作为基准值。
2) 减少递归次数
在已接近有序的递归最后一层或倒数第二层的待排序区间可以直接进行区间内插入排序,那么待排序区间的元素就不用每个再进行递归了。
注:当待排序数组元素过大时,递归进行快速排序可能会导致栈溢出,所以我们可以使用快速排序的非递归形式(使用栈或队列来模拟快速排序的递归)。
● 实现代码
/**
* 快速排序
* 时间复杂度:O(N*logN(以2为底))
* 空间复杂度:最好:O(logn(以2为底)) 最坏:O(N)
* 稳定性:不稳定
* @param arr 待排序数组
* @param left 每个区间最左边
* @param right 每个区间最右边
*/
public static void quickSort(int[] arr, int left, int right) {
if (left >= right) return;
//优化二:减少递归次数(选取的数字要根据待排序数组的元素个数选取,且尽可能的小)
if(right - left + 1 <= 4) {
//区间内插入排序
insertSort2(arr,left,right);
return;
}
//优化一:基准值选取
int midIndex = getMidIndex(arr,left,right);
swap(arr,left,midIndex);
// int pilot = getPilotIndex1(arr,left,right); //挖坑法
// int pilot = getPilotIndex2(arr,left,right); //hoare法
int pilot = getPilotIndex3(arr, left, right); //前后指针法
quickSort(arr, left, pilot - 1);
quickSort(arr, pilot + 1, right);
}
/**
* 区间内进行插入排序
* @param arr 待排序数组
* @param left 进行插入排序区间的第一个元素下标
* @param right 进行插入排序区间的最后一个元素下标
*/
private static void insertSort2(int[] arr, int left, int right) {
for (int i = left + 1; i <= right; i++) {
int temp = arr[i];
int j;
for (j = i - 1; j >= left; j--) {
if(arr[j] > temp) {
arr[j + 1] = arr[j];
}else break;
}
arr[j + 1] = temp;
}
}
/**
* 三数取中法
* @param arr 待选取数组
* @param left 第一个元素下标
* @param right 最后一个元素下标
* @return 三个数中的中间值的下标
*/
private static int getMidIndex(int[] arr, int left, int right) {
int mid = left + (right - left) / 2;
if(arr[left] < arr[right]) {
if(arr[mid] < arr[left]) {
return left;
}else if(arr[right] < arr[mid]) {
return right;
}else {
return mid;
}
}else {
if(arr[mid] < arr[right]) {
return right;
}else if(arr[left] < arr[mid]) {
return left;
}else {
return mid;
}
}
}
/**
* 挖坑法
* @param arr 待排序数组
* @param left 区间最左边
* @param right 区间最右边
* @return 当前基准值的正确所在位置
*/
private static int getPilotIndex1(int[] arr, int left, int right) {
int pilot = arr[left];
while (left < right) {
//右边找小
while (left < right && arr[right] >= pilot) right--;
arr[left] = arr[right];
//左边找大
while (left < right && arr[left] <= pilot) left++;
arr[right] = arr[left];
}
arr[left] = pilot;
return left;
}
/**
* hoare法
* @param arr 待排序数组
* @param left 区间最左边
* @param right 区间最右边
* @return 当前基准值的正确所在位置
*/
private static int getPilotIndex2(int[] arr, int left, int right) {
int pilot = arr[left];
int pilotIndex = left;
while (left < right) {
//右边找小
while (left < right && arr[right] >= pilot) right--;
//左边找大
while (left < right && arr[left] <= pilot) left++;
swap(arr, left, right);
}
swap(arr, left, pilotIndex);
return left;
}
/**
* 前后指针法
* @param arr 待排序数组
* @param left 区间最左边
* @param right 区间最右边
* @return 当前基准值的正确所在位置
*/
private static int getPilotIndex3(int[] arr, int left, int right) {
int pilot = arr[left];
int pre = left, cur = left + 1;
while (cur <= right) {
if(arr[cur] < pilot && arr[++pre] != arr[cur]) {
swap(arr, pre, cur);
}
cur++;
}
swap(arr, left, pre);
return pre;
}
/**
* 快速排序非递归实现
* @param arr 待排序数组
*/
public static void quickSort2(int[] arr) {
Deque<Integer> stack = new LinkedList<>();
stack.push(0);
stack.push(arr.length - 1);
while(!stack.isEmpty()) {
int right = stack.pop();
int left = stack.pop();
int pilotIndex = getPilotIndex1(arr,left,right);
//左区间有至少2个元素
if(pilotIndex > left + 1) {
stack.push(left);
stack.push(pilotIndex - 1);
}
//右区间有至少2个元素
if(pilotIndex < right - 1) {
stack.push(pilotIndex + 1);
stack.push(right);
}
}
}
7.归并排序
● 具体思路
① 将待排序数组不断分解,直到每个子区间只有一个元素。
② 分解后的子区间两两合并到中间数组中。
③ 将中间数组的元素值放入到待排序数组对应区间中。
注:其非递归思路–> 利用变量gap分组进行合并,找到left,mid,right和gap之间的关系,得到left,mid,right再不断进行合并,直到gap大于或等于待排序数组的长度,则停止合并。
● 排序过程演示
分解再合并的过程:
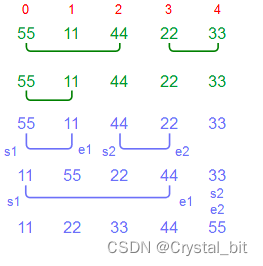
● 实现代码
/**
* 归并排序
* 时间复杂度:O(N*logN(以2为底))
* 空间复杂度:O(N)
* 稳定性:稳定
* @param arr 待排序数组
* @param start 起始位置
* @param end 终止位置
*/
public static void mergeSort(int[] arr, int start, int end) {
if (start >= end) return;
//分解
int mid = start + (end - start) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
//合并
merge(arr, start, mid, end);
}
private static void merge(int[] arr, int start, int mid, int end) {
int maxSize = end - start + 1;
int[] temp = new int[maxSize];
int k = 0;
int i = start, j = mid + 1;
while (i <= mid && j <= end) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
//子区间一有剩余
while (i <= mid) {
temp[k++] = arr[i++];
}
//子区间二有剩余
while (j <= end) {
temp[k++] = arr[j++];
}
for (int l = 0; l < maxSize; l++) {
arr[l + start] = temp[l];
}
}
/**
* 归并排序非递归实现
* @param arr 待排序数组
*/
public static void mergeSort(int[] arr) {
int gap = 1;
while (gap < arr.length) {
for (int i = 0; i < arr.length; i += 2 * gap) {
int left = i;
int mid = left + gap - 1;
if (mid >= arr.length) {
mid = arr.length - 1;
}
int right = mid + gap;
if (right >= arr.length) {
right = arr.length - 1;
}
merge(arr, left, mid, right);
}
gap *= 2;
}
}
8.基数排序
● 具体思路
① 根据待排序数组中元素范围值进行
中间数组temp的长度(max – min + 1)
确定。② 遍历待排序数组,将其每个元素值(-min)和中间数组temp下标形成映射关系,中间数组temp对应下标++(
temp数组中存放的是待排序数组中每个元素的个数
)。③ 遍历temp数组下标位置值不为零的元素,填入到待排序数组中(
对应下标+min则为待排序数组的元素值
)。
● 排序过程演示

● 实现代码
/**
* 计数排序
* 时间复杂度:O(N+范围)
* 空间复杂度:O(范围)
* 稳定性:不稳定
* @param arr 待排序数组
*/
public static void countSort(int[] arr) {
int max = arr[0], min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
if (arr[i] < min) {
min = arr[i];
}
}
int maxSize = max - min + 1;
int[] temp = new int[maxSize];
for (int i = 0; i < arr.length; i++) {
temp[arr[i] - min]++;
}
int index = 0;
for (int i = 0; i < maxSize; i++) {
int k = temp[i];
while (k > 0) {
arr[index++] = i + min;
k--;
}
}
}分享完毕。