两圆相切
如果两个圆恰有一个公共点,则称两圆相切。两圆相切分为内切(一个圆在另一个圆的内部)和外切(一个圆在另一个圆的外部)两种,如下图。设两圆为圆O,圆O’,半径为R,R’,则若两圆相切于点A,则:
(1) OO’=R+R’(两圆外切时),OO’=|R-R’|(两圆内切时);
(2)O,O’,A共线;
(3)过A的一个圆的切线为另一个圆的切线;
(4)若过A的直线与两圆交于B,C;B’,C’,则BC//B’C’。这是因为A为两圆位似中心,故B与B’,C与C’为相似对应点,从而AB/AB’=AC/AC’,则BC//B’C’。

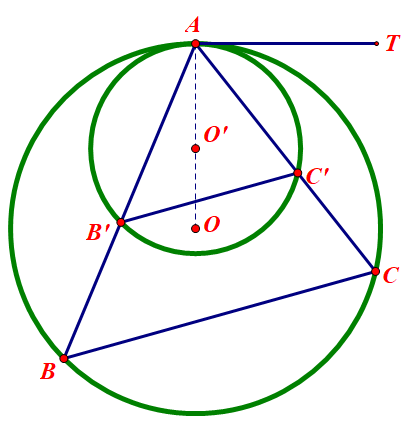
相反的,上述性质逆过来
即可判定两圆相切,即
(1)若两圆圆心O,O’及半径确定,则若OO’=R+R’则两圆外切,若OO’=|R-R’|,则两圆内切。
(2)若已知两圆圆心O,O’及一个公共点A,若O,O’,A共线,则两圆相切。
(3)若已知两圆的一个公共点A,过A的一个圆的切线为另一个圆的切线,则两圆相切。
(4)过A的直线与两圆交于B,C;B’,C’,若BC//B’C’则两圆相切于A。这是因为△ABC和△A’B’C’以A为位似中心位似,故他们的外接圆也以A为位似中心位似,故两圆相切于A。
不难发现上述判定中(2)和(3)是等价的。
这些性质和判定都很简单,但是要运用这些判定来判定两个圆,特别是要证明三角形的外接圆与某个圆相切,一般都是比较困难的。下面看一些与两圆相切的性质和判定有关的一些问题。这些题目看起来还是比较恐怖的,很多题目也是非常复杂的,此类问题往往都是各类竞赛的压轴题。关于这个专题的文章相对较少,我写过一篇[1],有兴趣的读者可以参考。