基于密度聚类方法(DBSCAN算法)
密度聚类方法的指导思想: 只要样本点的密度大于某个阈值,则将该样本添加到最近的簇中;
- 优点:这类算法可以克服基于距离的算法只能发现凸聚类的缺点,可以发现任意形状的聚类,而且对噪声数据不敏感。
- 缺点:计算复杂度高,计算量大
常用算法:DBSCAN、密度最大值算法
DBSCAN算法(Density-Based Spatial Clustering of Applications withNoise)
DBSCAN算法是一个比较有代表性的基于密度的聚类算法,相比于基于划分的聚类方法和层次聚类方法,
DBSCAN算法将簇定义为密度相连的点的最大集合
,能够将足够高密度的区域划分为簇,并且在具有噪声的空间数据商能够发现任意形状的簇。
DBSCAN算法的
核心思想
是:
用一个点的ε邻域内的邻居点数衡量该点所在空间的密度
,该算法可以找出形状不规则的cluster,而且聚类的时候事先不需要给定cluster的数量
DBSCAN算法基本概念
-
ε邻域(ε neighborhood,也称为Eps):给定对象在半径ε内的区域
Nε
=
y
∈
X
:
d
i
s
t
(
x
,
y
)
≤
ε
N_{ε} = {y∈X:dist(x,y)≤ε}
N
ε
=
y
∈
X
:
d
i
s
t
(
x
,
y
)
≤
ε
-
密度(density):ε邻域中x的密度,是一个整数值,依赖于半径ε
p(
x
)
=
∣
N
ε
(
x
)
∣
p(x) = |N_{ε}(x)|
p
(
x
)
=
∣
N
ε
(
x
)
∣
- MinPts定义核心点时的阈值,也简记为M
-
核心点(core point):如果
p(
x
)
>
=
M
p(x)>=M
p
(
x
)
>=
M
,那么称x为X的核心点;记由X中所有核心点构成的集合为
Xc
X_{c}
X
c
,并记
Xc
=
X
\
X
c
X_{c}=X\backslash X_{c}
X
c
=
X
\
X
c
表示由X中所有非核心点构成的集合。直白来讲,核心点对应于稠密区域内部的点。 -
边界点(border point): 如果非核心点x的ε邻域中存在核心点,那么认为x为X的边界点。由X中所有的边界点构成的集合为
Xb
d
X_{bd}
X
b
d
。直白来将,边界点对应稠密区域边缘的点。
x∈
X
n
c
;
ヨ
y
∈
X
;
y
∈
N
ε
(
x
)
∩
X
c
x∈X_{nc};ヨy∈X;y∈N_{ε}(x)∩X_{c}
x
∈
X
n
c
;
ヨ
y
∈
X
;
y
∈
N
ε
(
x
)
∩
X
c
-
噪音点(noise point):集合中除了边界点和核心点之外的点都是噪音点,所有噪音点组成的集合叫做
Xn
o
i
X_{noi}
X
n
o
i
;直白来讲,噪音点对应稀疏区域的点。
Xn
o
i
=
X
\
(
X
c
∪
X
b
d
)
X_{noi} = X\backslash(X_{c}∪X_{bd})
X
n
o
i
=
X
\
(
X
c
∪
X
b
d
)
-
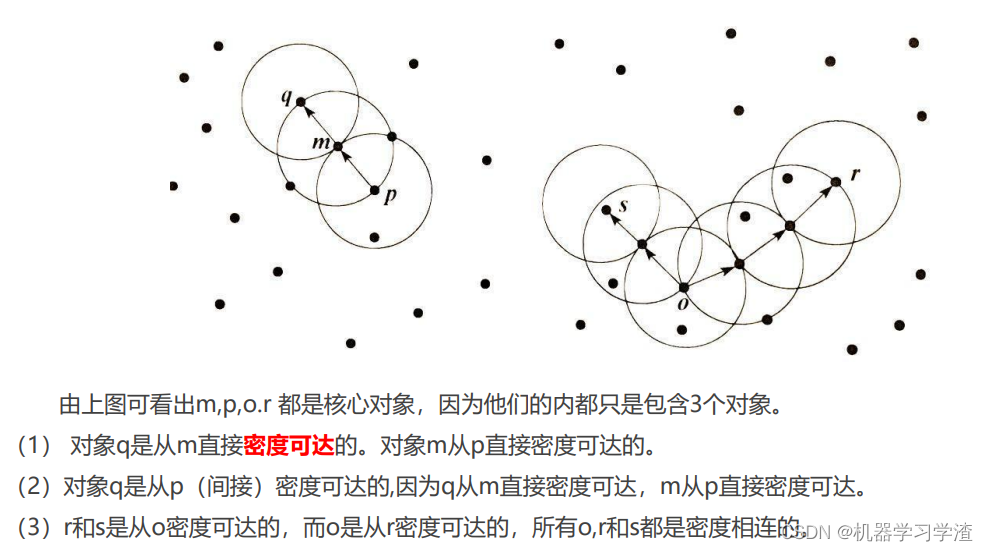
直接密度可达(directly density-reachable):给定一个对象集合X,如果y是在x的ε邻域内,而且x是一个核心对象,可以说对象y从对象x出发是直接密度可达的
x,
y
∈
X
;
x
∈
X
c
,
y
∈
N
ε
(
x
)
x,y∈X;x∈X_{c},y∈N_{ε}(x)
x
,
y
∈
X
;
x
∈
X
c
,
y
∈
N
ε
(
x
)
-
密度可达(density-reachable):如果存在一个对象链
p1
p_{1}
p
1
,
p2
p_{2}
p
2
,…
pm
p_{m}
p
m
,如果满足
pi
+
1
p_{i+1}
p
i
+
1
是从
pi
p_{i}
p
i
直接密度可达的,那么称
pm
p_{m}
p
m
,是从
p1
p_{1}
p
1
密度可达的. - 密度相连(density-connected):在集合X中,如果存在一个对象o,使得对象x和y是从o关于ε和m密度可达的,那么对象x和y是关于ε和m密度相连的
-
簇(cluster):一个基于密度的簇是最大的密度相连对象的集合C;满足以下两个条件:
- Maximality:若x属于C,而且y是从x密度可达的,那么y也属于C
- Connectivity:若x属于C,y也属于C,则x和y是密度相连的
例子:
DBSCAN算法流程
算法流程:
- 如果一个点x的ε邻域包含多余m个对象,则创建一个x作为核心对象的新簇;
- 寻找并合并核心对象直接密度可达的对象;
- 没有新点可以更新簇的时候,算法结束。
算法特征描述:
- 每个簇至少包含一个核心对象
- 非核心对象可以是簇的一部分,构成簇的边缘
- 包含过少对象的簇被认为是噪声
DBSCAN算法优缺点
-
优点:
- 不需要事先给定cluster的数目
- 可以发现任意形状的cluster
- 能够找出数据中的噪音,且对噪音不敏感
- 算法只需要两个输入参数
- 聚类结果几乎不依赖节点的遍历顺序
-
缺点:
- DBSCAN算法聚类效果依赖距离公式的选取,最常用的距离公式为欧几里得距离。但是对于高维数据,由于维数太多,距离的度量已变得不是那么重要
- DBSCAN算法不适合数据集中密度差异很小的情况
密度聚类算法(DBSCAN算法)案例
使用scikit的相关API创建模拟数据,然后使用DBSCAN密度聚类算法进行数据聚类操作,并比较DBSCAN算法在不同参数情况下的密度聚类效果
# 导包
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
## 设置属性防止中文乱码及拦截异常信息
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
### 创建模拟数据
N = 1000
# 生成以[1, 2], [-1, -1], [1, -1], [-1, 1]为中心,方差为1,0.75, 0.5,0.25的四个数据集
centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
data1, y1 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1,0.75, 0.5,0.25), random_state=0)
data1 = StandardScaler().fit_transform(data1)
params1 = ((0.15, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))
# 生成以三个圆环数据集
t = np.arange(0, 2 * np.pi, 0.1)
data2_1 = np.vstack((np.cos(t), np.sin(t))).T
data2_2 = np.vstack((2*np.cos(t), 2*np.sin(t))).T
data2_3 = np.vstack((3*np.cos(t), 3*np.sin(t))).T
data2 = np.vstack((data2_1, data2_2, data2_3))
y2 = np.vstack(([0] * len(data2_1), [1] * len(data2_2), [2] * len(data2_3)))
params2 = ((0.5, 3), (0.5, 5), (0.5, 10), (1., 3), (1., 10), (1., 20))
datasets = [(data1, y1,params1), (data2, y2,params2)]
# 画图用的横坐标轴范围
def expandBorder(a, b):
d = (b - a) * 0.1
return a-d, b+d
colors = ['r', 'g', 'b', 'y', 'c', 'k']
cm = mpl.colors.ListedColormap(colors)
### 画图
for i,(X, y, params) in enumerate(datasets):
x1_min, x2_min = np.min(X, axis=0)
x1_max, x2_max = np.max(X, axis=0)
x1_min, x1_max = expandBorder(x1_min, x1_max)
x2_min, x2_max = expandBorder(x2_min, x2_max)
plt.figure(figsize=(12, 8), facecolor='w')
plt.suptitle(u'DBSCAN聚类-数据%d' % (i+1), fontsize=20)
plt.subplots_adjust(top=0.9,hspace=0.35)
for j,param in enumerate(params):
eps, min_samples = param
model = DBSCAN(eps=eps, min_samples=min_samples)
#eps 半径,控制邻域的大小,值越大,越能容忍噪声点,值越小,相比形成的簇就越多
#min_samples 原理中所说的M,控制哪个是核心点,值越小,越可以容忍噪声点,越大,就更容易把有效点划分成噪声点
model.fit(X)
y_hat = model.labels_
unique_y_hat = np.unique(y_hat)
n_clusters = len(unique_y_hat) - (1 if -1 in y_hat else 0)
print ("类别:",unique_y_hat,";聚类簇数目:",n_clusters)
core_samples_mask = np.zeros_like(y_hat, dtype=bool)
core_samples_mask[model.core_sample_indices_] = True
## 开始画图
plt.subplot(3,3,j+1)
for k, col in zip(unique_y_hat, colors):
if k == -1:
col = 'k'
class_member_mask = (y_hat == k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col, markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col, markeredgecolor='k', markersize=6)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.title('$\epsilon$ = %.1f m = %d,聚类簇数目:%d' % (eps, min_samples, n_clusters), fontsize=16)
## 原始数据显示
plt.subplot(3,3,7)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.title('原始数据,聚类簇数目:%d' % len(np.unique(y)))
plt.grid(True)
plt.show()