“
单个总体均值的区间估计和相应的蒙特卡罗模拟
”
设想一下这样的场景:现有一大批零件,我们想了解这批零件的某个特性(比如长度)的平均值,该用什么办法呢?如果全部测量将会耗费大量人力物力,现实的做法往往是从中随机抽取少量的零件进行测量,根据获得的样本数据估计总体均值。本文讨论具有类似性质的问题,即如何根据样本观测值估计总体均值。
01
—
总体均值的置信区间
大样本
当样本数量n≥30时,该样本可视为大样本。根据中心极限定理,选择标准正态随机变量Z作为枢轴统计量,则总体均值的区间估计方法如下:

在大多数情况下,总体标准差σ是未知的,因此通常使用样本标准差s作为总体标准差的估计量,下同。
小样本
如果样本属于小样本,并且总体近似正态分布,可以使用T统计量做为枢轴统计量,此时总体均值的区间估计方法如下:

注意:对于小样本,当总体严重偏离正态分布时,这种估计方法可能存在偏差,推荐使用其他的估计方法。
02
—
蒙特卡罗模拟
小样本估计总体均值
1)总体为正态分布
假设总体是均值为5,方差为1的正态分布,从中随机抽取10个样本,试根据样本观测值求总体均值的95%的置信区间。
①生成随机数(每次试验生成10个观测值,进行100个重复试验)
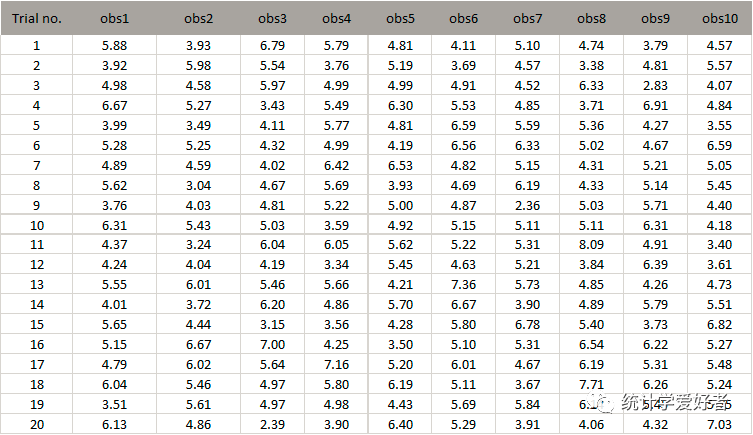
②根据规则构造总体均值的置信区间,检查成功捕获的区间比例
可以发现,成功捕获总体的区间在95%左右
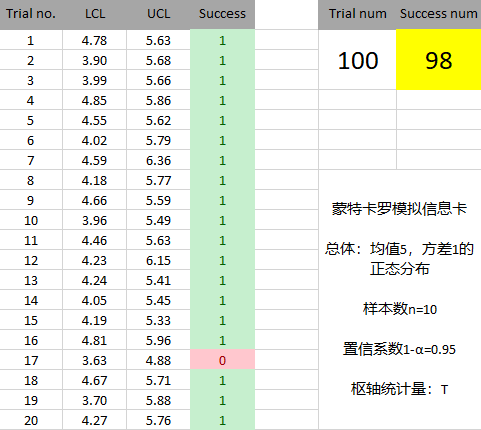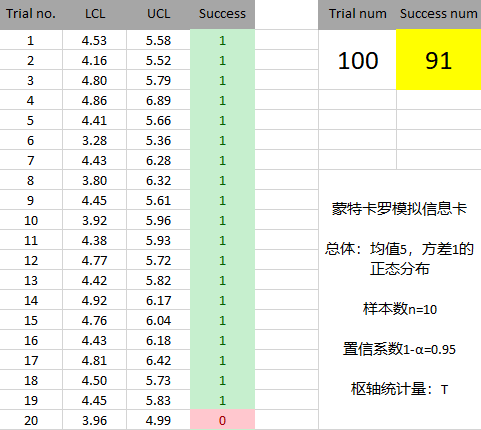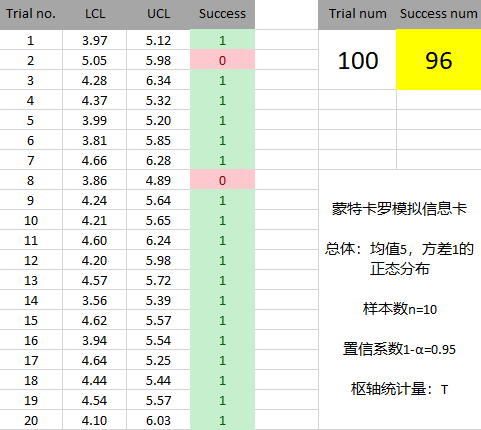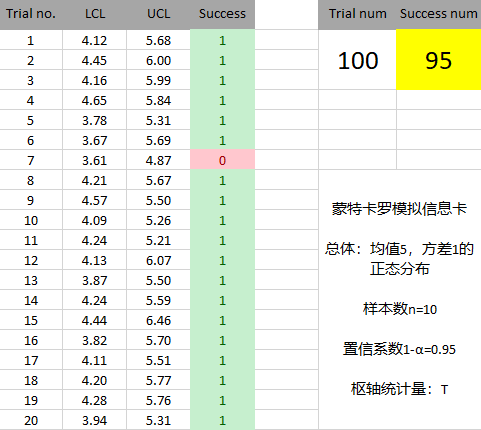
2)总体为指数分布(严重偏离正态性)
假设总体是均值为5的指数分布,从中随机抽取10个样本,试根据样本观测值求总体均值的95%的置信区间。
①生成随机数
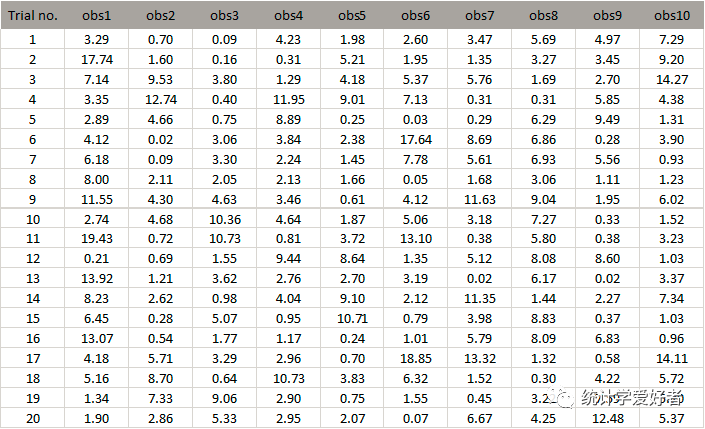
②根据规则构造置信区间,检查成功捕获总体均值的区间比例
从结果来看,成功捕获总体均值的区间比例很可能小于95%
