从单一元素的异或解法到HashMap源码
有序数组中的单一元素
来自力扣原题:
给你一个仅由整数组成的有序数组,其中每个元素都会出现两次,唯有一个数只会出现一次。
请你找出并返回只出现一次的那个数。
你设计的解决方案必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。
示例 1:
输入: nums = [1,1,2,3,3,4,4,8,8]
输出: 2
示例 2:
输入: nums = [3,3,7,7,10,11,11]
输出: 10
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/single-element-in-a-sorted-array
普通解法
这道题其实很简单,就是跳两下判断下一个数是否和当前数相同就好了。
class Solution {
public int singleNonDuplicate(int[] nums) {
// 原来我就是单一元素 22.2.14简记
for(int i = 0; i < nums.length-1; i += 2){
if(nums[i] != nums[i+1]){
return nums[i];
}
}
return nums[nums.length - 1];
}
}
异或解法
做完奔着题解区看看别人的想法,没想到有个异或的题解是真滴帅。
class Solution {
public int singleNonDuplicate(int[] nums) {
// 原来我就是单一元素 22.2.14简记
int ans = 0;
for (int i = 0; i < nums.length; i++){
ans ^= nums[i];
}
return ans;
}
}
异或概念
一开始我也是不清楚异或的概念的,于是上网查了下:
异或的运算法则为:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同为0,异为1)
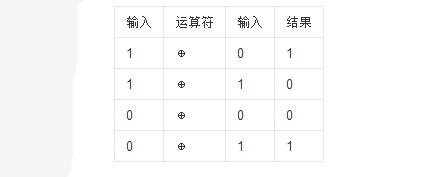
demo:
0011
1110 异或运算后是:
1101
简单说就是两个数不相等为1,相等为0
简单的说完了异或的概念,在解析下是如何把刚才的单一元素解出来的。
如[1,1,2,3,3]
// 初始值ans给个0,1的二进制是0001,于是:
0000 ^
0001 = 0001
// 1和1在异或运算,就变回0了
0001^
0001 = 0000
// 0和1做运算,变成1
0001 ^
0010 = 0010
// 2的二进制是0011,异或变成1
0010 ^
0011 = 0001
// 最后异或运算成为2
0001 ^
0011 = 0010
那么我们最后返回的是nums[ans],也就是在第二位的数,正确的返回了我们想要的单一元素。
异或运算多应用于加密、寻找单一元素上,这里不在多讲,感兴趣的朋友可以自己拓展。
HashMap是如何使用异或的呢
学会异或运算后,突然想起了曾经在HashMap的源码中看到过使用,只不过当时懵懵懂懂没深入研究,那么就现在乘胜追击吧~
在HashMap中,用hash算法或得存取位置无疑是最重要的一步,而在hash算法中就用到了异或运算,我们来看看这里是如何巧妙设计的。
源码
方法一:
static final int hash(Object key) { //jdk1.8 & jdk1.7
int h;
// h = key.hashCode() 为第一步 取hashCode值
// h ^ (h >>> 16) 为第二步 高位参与运算
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
方法二:
static int indexFor(int h, int length) { //jdk1.7的源码,jdk1.8没有这个方法,但是实现原理一样的
return h & (length-1); //第三步 取模运算
}
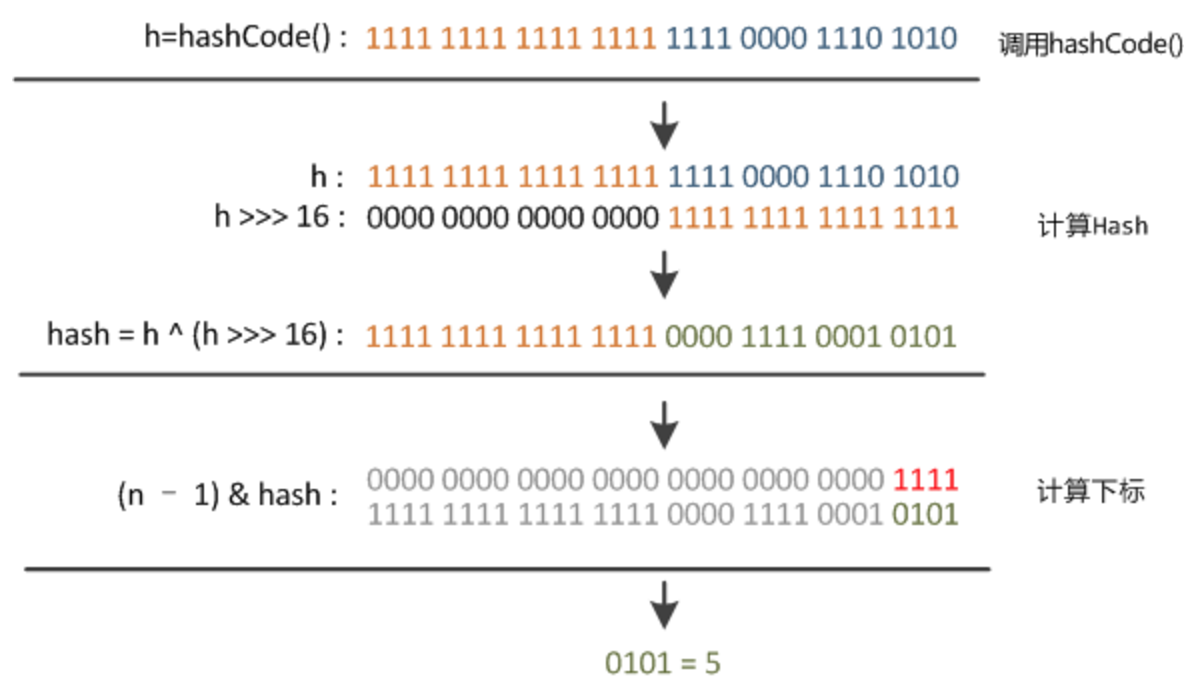
流程图解
来源美团技术团队
思考
首先想明白,为什么已经用hashCode()方法取到哈希值了,还需要继续 ^ (h >>> 16)。
这是因为只用后四位数进行运算,非常容易产生大量的hash碰撞,于是将高16位右移,并且
异或
计算。
那么打破砂锅问到底,为什么用异或^
我查阅了挺多文章,都说是右移16位异或可以同时保留高16位于低16位的特征。并且如果采用&运算计算出来的值会向1靠拢,采用|运算计算出来的值会向0靠拢。用异或则能让01能更随机的出现,而不趋向某一边。
一开始不太懂,后来想到作者的想法应该是:
让哈希后的结果更均匀的分布,减少哈希碰撞,提升hashmap的运行效率
就想到了,保留两边的特征反而能让hash值更离散或者说随机,尽可能的减少了hash碰撞。
参考
主要参考:
https://tech.meituan.com/2016/06/24/java-hashmap.html
本章源码解析参考:
https://blog.csdn.net/dam454450872/article/details/102965920
https://blog.csdn.net/weixin_43842753/article/details/105927912
https://tech.meituan.com/2016/06/24/java-hashmap.html