e的泰勒展开式(麦克劳林展开式):
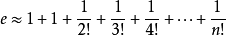
//计算自然常数e的公式为e的泰勒展开式(麦克劳林展开式)
#include<iostream>
using namespace std;
const double MaxError = 1.0E-6; //误差上限
long int GetFactorial(int n) //用for循环计算阶乘
{
if (n == 0)
return 1;
else
{
int i, j = 1;
for (i = 1; i <= n; i++)
j *= i;
return j;
}
}
double GetE(int n) //根据泰勒展开式计算自然常数e
{
int i;
long int k;
double sum = 0, j; //sum为计算e的和式
for (i = 0; i < n; i++)
{
k = GetFactorial(i);
j = 1.0 / k;
sum = sum + j;
}
return sum;
}
int main()
{
double e = 2.178281;
double R=1.0; //R为计算e的拉格朗日型余项(Remainder)的上确界,其初始值设为e的泰勒展开式的第二项
int n = 1, num = 1; //num为e的泰勒展开式的项数
while (R > MaxError) //当余项R小于误差上限时跳出循环
{
num++;
n++;
R = e / GetFactorial(n);
}
cout <<"当泰勒展开式到第"<< num <<"项时余项R小于1.0E-6" << endl;
cout << "此时自然常数e为"<<GetE(num) << endl;
return 0;
}
程序运行到最后,余项R,项数num,按照泰勒展开式计算e的和式sum的值如下图所示。

真实的e ≈ 2.718281828459045
版权声明:本文为Nothing_f原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。