概述
由于二叉树的结构会受到添加数据的顺序的影响,最坏情况下会退化成一个单链表,这样就会严重影响二叉树的操作的性能,为了解决这个问题,就需要引入一种平衡机制,让整个二叉树总体上保持平衡的状态,具有自动保证平衡的特性的二叉树就叫做平衡二叉树。
平衡二叉树中设计到两个比较重要的概念:
- 节点的高度:某个节点的高度=它的子节点的最大高度+1,一个节点的默认高度是1,空节点的高度是0
- 平衡因子:左右子树的高的差,比如左子节点的高度为2,右子节点的高度为1,那么当前节点的平衡因子就是1,当某个节点的平衡因子>1时,以这个节点为根节点的树就一定发生了倾斜,那么整颗二叉树就处于一种不平衡的状态。
平衡二叉树是通过旋转的方式来实现树的动态平衡的,不平衡的情况主要有以下四种:
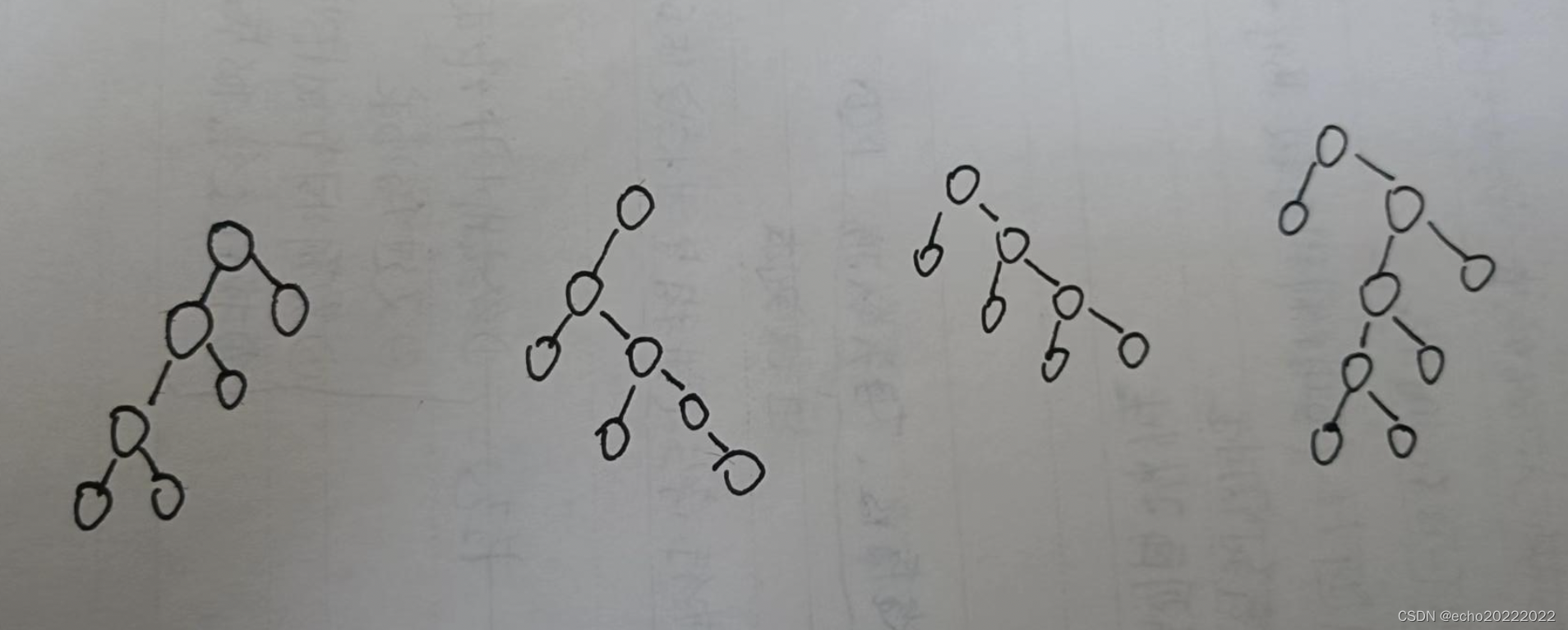
- 一直向左倾斜
- 左子节点向右倾斜
- 一直想右倾斜
- 右子节点向左倾斜
一直向左倾斜
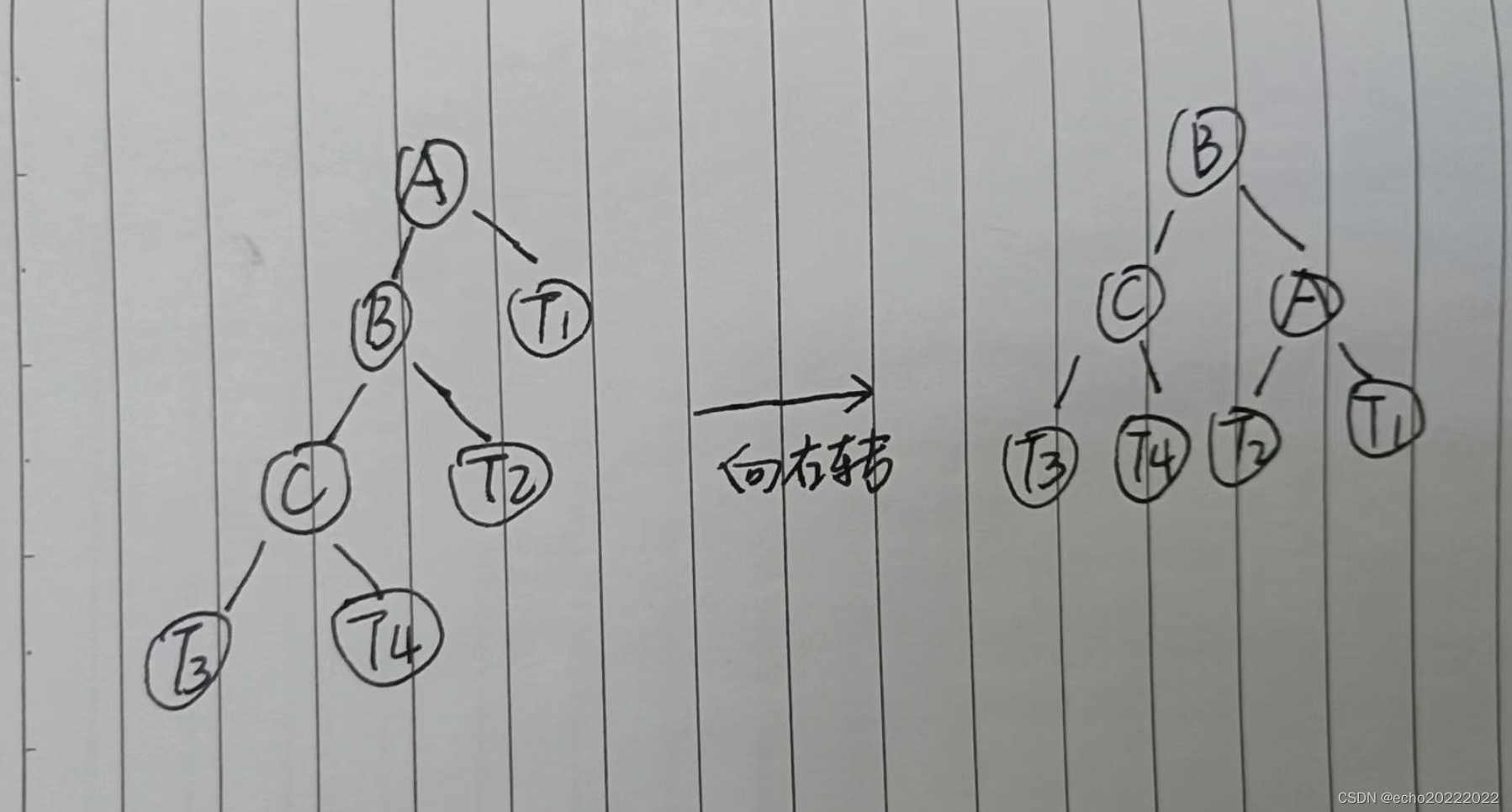
左子节点向右倾斜
这种情况需要先左旋,再右旋转
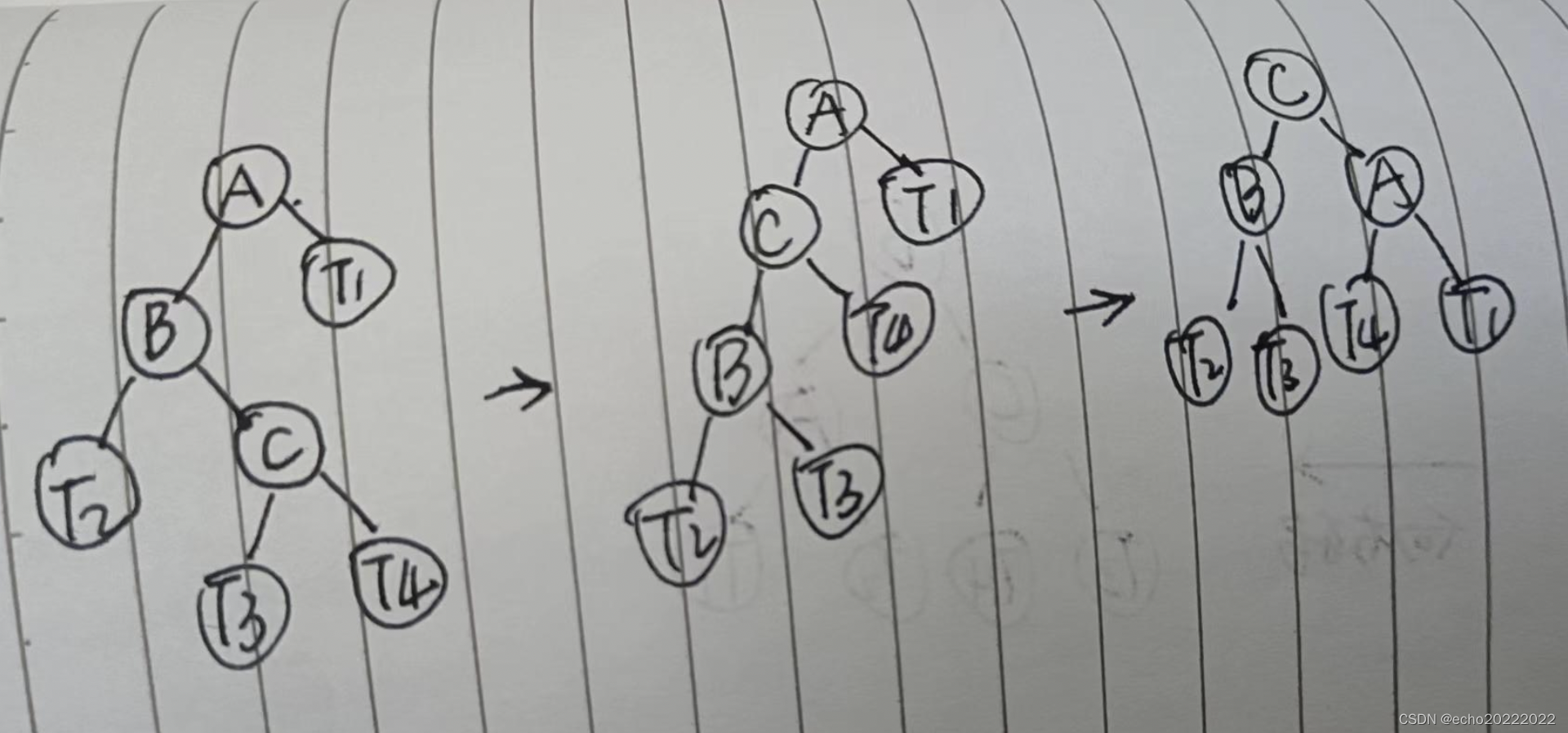
一直想右倾斜
相对于一直向左旋转来说,这种情况需要向左旋转一次。
右子节点向左倾斜
相对于左节点向右倾斜来说,这钱情况需要先向右旋转一次,再向左旋转一次。
代码实现
由于只有在添加和删除节点的时候会破坏树的平衡性,所以只需要关注这两个操作就可以,具体过程是:
- 计算节点的高度
- 计算节点的平衡因子
- 旋转树,保证平衡
修改节点结构
private static class Node<E extends Comparable<E>>{
private E data;
private Node<E> left;
private Node<E> right;
//节点的高度,默认值为1
private int height;
public Node(E elem) {
this(elem, null, null);
}
public Node(E elem, Node<E> left, Node<E> right) {
this.left = left;
this.right = right;
this.data = elem;
this.height = 1;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
}
添加辅助函数
/**
* 一些辅助函数
* */
/**
* 右旋转
y
x t4
z t3
t1 t2
->>>>>
x
z y
t1 t2 t3 t4
* */
private Node<E> rightRotate(Node y) {
Node<E> x = y.left;
Node<E> t3 = x.right;
x.right = y;
y.left = t3;
//更新x和y的高度
y.height = 1 + Math.max(getHeight(y.left), getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return x;
}
/**
同理,左旋转,处理向右倾斜的情况
y
t4 x
t3 z
t2 t1
>>>>>>
x
y z
t4 t3 t2 t1
x.left = y
y.right = t3
* */
public Node<E> leftRotate(Node y) {
Node<E> x = y.right;
Node<E> t3 = x.left;
x.left = y;
y.right = t3;
//更新y和x的高度,注意先更新y值的高度,再更新x值的高度
y.height = 1 + Math.max(getHeight(y.left), getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return x;
}
//获取当前节点的高度值
private int getHeight(Node<E> node) {
if(node == null) {
return 0;
}
return node.height;
}
//计算当前节点的平衡因子
private int getBalanceFactor(Node<E> node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
//判断二分搜索树是否平衡
private boolean isBalanced() {
return isBalanced(root);
}
private boolean isBalanced(Node<E> node) {
//到底了
if (node == null) {
return true;
}
//计算当前节点的平和因子
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
完整实现
package com.base.ds.csdn.tree;
import java.util.LinkedList;
import java.util.Queue;
/**
* 二分搜索树.
* 特点:左子节点 < 根节点 < 右子节点.
* 操作:
* 1. 添加
* 2. 删除
* 3. 遍历(前、中、后序遍历、层序遍历)
* */
public class AVLTree<E extends Comparable<E>> {
private Node<E> root;
private int size;
//初始化
public AVLTree() {
this.root = null;
size = 0;
}
/**
* 添加数据.
* */
public void add(E e) {
//添加操作完成后,root节点可能发生变化
root = add(e, root);
}
//利用递归,添加节点
private Node<E> add(E e, Node<E> node) {
if (node == null) {
size ++;
return new Node(e);
}
//如果当前数据比当前节点的值小,则向左添加
if(e.compareTo(node.data) < 0) {
node.left = add(e, node.left);
} else if (e.compareTo(node.data) > 0) {
node.right = add(e, node.right);
}
//return node;
//更新当前节点的高度
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
//计算当前节点的平和因子
//平衡因子要保持正负符号,因为要区分向左或向右倾斜
int balanceFactor = getBalanceFactor(node);
//如果发生了倾斜
if (Math.abs(balanceFactor) > 1) {
//LL
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
//右旋转后,返回新的根
return rightRotate(node);
}
//RR
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
//向右倾斜,进行左旋转
return leftRotate(node);
}
//LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
//左旋转
node.left = leftRotate(node.left);
//右旋转
return rightRotate(node);
}
//RL
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
//右旋转
node.right = rightRotate(node.right);
//左旋转
return leftRotate(node);
}
}
}
/**
* 判断释放包含某个数据
* */
public boolean contains(E e) {
if (isEmpty()) {
throw new IllegalArgumentException("bst is empty.");
}
return contains(e, root);
}
//利用递归来判断释放包含
private boolean contains(E e, Node<E> node) {
if (node == null) {
return false;
}
if (e.compareTo(node.data) == 0) {
return true;
} else if (e.compareTo(node.data) < 0) {
return contains(e, node.left);
} else {
return contains(e, node.right);
}
}
/**
* 找到最小的数据
* */
public E min() {
if (isEmpty()) {
throw new IllegalArgumentException("bst is empty.");
}
return minNode(root).data;
}
private Node<E> minNode(Node<E> node) {
if (node.left == null) {
return node;
}
return minNode(node.left);
}
/**
* 找到最大的数据
* */
public E max() {
if (isEmpty()) {
throw new IllegalArgumentException("bst is empty.");
}
return maxNode(root).data;
}
private Node<E> maxNode(Node<E> node) {
if (node.right == null) {
return node;
}
return maxNode(node.right);
}
/**
* 删除最小值
* */
public E removeMin() {
E ret = min();
root = removeMin(root);
return ret;
}
//用递归的方式实现
private Node<E> removeMin(Node<E> node) {
if (node.left == null) {
Node<E> right = node.right;
node.right = null;
size --;
return right;
}
node.left = removeMin(node.left);
return node;
}
/**
* 删除最大值
* */
public E removeMax() {
E ret = max();
root = removeMax(root);
return ret;
}
private Node<E> removeMax(Node<E> node) {
if (node.right == null) {
Node<E> left = node.left;
node.left = null;
size --;
return left;
}
node.right = removeMax(node.right);
return node;
}
/**
* 移除给定值的节点
* */
public void remove(E e){
root = remove(e, root);
}
private Node<E> remove(E e, Node<E> node) {
//如果没有找到目标节点就直接范围null
if (node == null) {
return null;
}
Node<E> retNode ;
//给定值比当前节点的值小
if (e.compareTo(node.data) < 0) {
node.left = remove(e, node.left);
retNode = node;
} else if (e.compareTo(node.data) > 0) {
//给定值比当前节点的值大
node.right = remove(e, node.right);
retNode = node;
} else {
//找到了要删除的节点
/**
* 没有左子节点
* 没有右子节点
* 即有左子节点也有右子节点
* */
//没有左子树
if (node.left == null) {
Node<E> right = node.right;
node.right = null;
size --;
retNode = right;
}
//没有右子树
if (node.right == null) {
Node<E> left = node.left;
node.left = null;
size --;
retNode = left;
}
//即有左子树又有右子树
//思路是:用左子树中的最大节点 或 用右子树中的最小节点来替换删除的节点,这样可以
//保证二叉搜索树的性质
//找到又子树中的最小节点
Node<E> rightMinNode = minNode(node.right);
//将右子树中的最小节点删除,并把删除后的新的根节点挂在 上面得到的Node的右侧分支
rightMinNode.right = removeMin(node.right);
//将当前待删除节点的left挂到rightMinNode上
rightMinNode.left = node.left;
//help GC
node.right = null;
node.left = null;
retNode = rightMinNode;
}
//如果删除的是叶子节点,不用维护平衡
if (retNode == null) {
return null;
}
//更新高度
retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
//计算当前节点的平衡因子,看是否需要旋转
int balanceFactor = getBalanceFactor(retNode);
if (Math.abs(balanceFactor) > 1) { //左右高度差 > 1,就需要进行旋转
//LL
if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
//右旋转后,返回新的根
return rightRotate(retNode);
}
//RR
if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
//向右倾斜,进行左旋转
return leftRotate(retNode);
}
//LR
if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
//左旋转
retNode.left = leftRotate(retNode.left);
//右旋转
return rightRotate(retNode);
}
//RL
if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
//右旋转
retNode.right = rightRotate(retNode.right);
//左旋转
return leftRotate(retNode);
}
}
return retNode;
}
/**
* 一些辅助函数
* */
/**
* 右旋转
y
x t4
z t3
t1 t2
->>>>>
x
z y
t1 t2 t3 t4
* */
private Node<E> rightRotate(Node y) {
Node<E> x = y.left;
Node<E> t3 = x.right;
x.right = y;
y.left = t3;
//更新x和y的高度
y.height = 1 + Math.max(getHeight(y.left), getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return x;
}
/**
同理,左旋转,处理向右倾斜的情况
y
t4 x
t3 z
t2 t1
>>>>>>
x
y z
t4 t3 t2 t1
x.left = y
y.right = t3
* */
public Node<E> leftRotate(Node y) {
Node<E> x = y.right;
Node<E> t3 = x.left;
x.left = y;
y.right = t3;
//更新y和x的高度,注意先更新y值的高度,再更新x值的高度
y.height = 1 + Math.max(getHeight(y.left), getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return x;
}
//获取当前节点的高度值
private int getHeight(Node<E> node) {
if(node == null) {
return 0;
}
return node.height;
}
//计算当前节点的平衡因子
private int getBalanceFactor(Node<E> node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
//判断二分搜索树是否平衡
private boolean isBalanced() {
return isBalanced(root);
}
private boolean isBalanced(Node<E> node) {
//到底了
if (node == null) {
return true;
}
//计算当前节点的平和因子
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
/**
* 前序遍历:父节点、左节点、右节点
* 中序遍历:左节点、父节点、右节点
* 后续遍历:左节点、右节点、父节点
* 层序遍历:一层一层遍历
* */
//前
public void preOrder() {
preOrder(root);
}
private void preOrder(Node<E> node) {
if (node == null) {
return;
}
System.out.println(node.data);
preOrder(node.left);
preOrder(node.right);
}
//中
public void inOrder() {
inOrder(root);
}
private void inOrder(Node<E> node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.println(node.data);
inOrder(node.right);
}
//后
public void postOrder() {
postOrder(root);
}
private void postOrder(Node<E> node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.data);
}
//层序遍历,借助队列
public void levelOrder() {
if (root == null) {
return;
}
Queue<Node<E>> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty() && root != null) {
Node<E> cur = queue.remove();
System.out.println(cur.data);
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}
public boolean isEmpty() {
return size == 0;
}
private static class Node<E extends Comparable<E>>{
private E data;
private Node<E> left;
private Node<E> right;
private int height;
public Node(E elem) {
this(elem, null, null);
}
public Node(E elem, Node<E> left, Node<E> right) {
this.left = left;
this.right = right;
this.data = elem;
this.height = 1;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
}
}
版权声明:本文为echoagod原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。