问题描述
:
以4皇后为例,其他的N皇后问题以此类推。所谓4皇后问题就是求解如何在4×4的棋盘上无冲突的摆放4个皇后棋子。在国际象棋中,皇后的移动方式为横竖交叉的,因此在任意一个皇后所在位置的水平、竖直、以及45度斜线上都不能出现皇后的棋子。
回溯法
:
dfs+迭代
1.如何判断当前位置的取值满足条件:
假设一个变量,每次设值都与前面已经设置好了的皇后的位置进行比较,是否同行同列,同斜线可以使用表达式:a[i]=a[j]=i-j || a[i]-a[j]=j-i
2.什么情况下成功找到四皇后的摆放位置:
当i>4,也就是当前设值的位置已经是最后一个皇后了并且设置的位置也能满足条件
3.什么情况下四个皇后还没有全部确定完,还需要进行查找下一个:
当i=1并且i<4时,这时候还有皇后没有确定位置,还需要进行查找
4.什么情况下进行回溯:
当i=0时并且a[i]=4并且i>1时,ok=0表示当前位置的值不能满足,a[i]=4表示当前位置所有的值都设置过了仍然没有满足条件的,i>1表示还可以进行回溯,如果i=1时表示它是第一个皇后,就没有进行回溯的对象了,那程序就可以终止了
5.什么情况下探索完毕,程序终止:
当a[i]=4并且i=1时,已经没有回溯的对象了,这时候程序就终止了
#include<iostream>
#define N 4
using namespace std;
void Print(int n, int a[])
{
for (int j = 1; j <= n; j++)
cout << a[j] << " "; //输出最终的棋盘布局,每个数组元素值表示各行棋盘所在的该列放置皇后
cout << endl;
}
int isOk(int i, int a[])
{ //检查当前棋盘布局是否合理
for (int j = i - 1; j>= 1; j--)
if (a[i] == a[j] || abs(a[i] - a[j]) == i - j)
return 0;
return 1;
}
void queen(int i, int n, int a[]) { //进入本函数前,前i-1行已经放置了互不攻击的i-1个皇后
if (i > n)
Print(n, a); //如果i已经大于最大的行数了,那么说明布局完成,则打印结果
else {
for (int j = 1; j <= n; j++) {
a[i] = j; //在第i行第j列放置一个皇后
if (isOk(i, a))
queen(i + 1, n, a); //当前布局合理,进行下一行的布局
a[i] = 0; //移走第i行第j列放置的皇后, 回溯。
}
}
}
int main()
{
int ct[N] = { 0 }; //棋盘的初始状态,棋盘上无任何皇后
queen(1, N, ct); //摆放皇后
return 0;
}
分支限界法
:
剪枝
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int count = 1;
struct Node
{
int no; //结点编号
int row; //结点行号
vector<int>cols; //用来存储结点列号
};
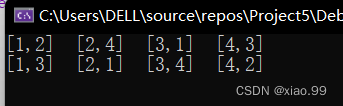
int Print(Node e) //输出一个结点的内容
{
if (e.row != -1)
cout << "编号为" << e.no <<"对应位置" << "[" << e.row << "," << e.cols[e.row] << "]" << endl;
return 0;
}
int isOK(vector<int> cols, int i, int j) //测试(i,j)这个结点能否放在棋盘上作为皇后
{
for (int k = 0;k < i;k++)
{
if ((cols[k] == j) || abs(cols[k] - j) == abs(k - i))
return 0;
}
return 1;
}
void queen()
{
int i, j, count = 1;
Node e, e1; //定义两个结点
queue<Node>qu; //定义一个结点
e.no = count++; //建立一个根节点,虚结点,它的row=-1,进入qu队列
e.row = -1;
qu.push(e); //根节点入队
while (!qu.empty()) //队列不空的时候进入循环
{
e = qu.front(); //出队结点作为当前结点
qu.pop();
if (e.row == 3) //到达叶子节点
{
cout << "产生一个解:"<<endl;
for (i = 0; i < 4; i++) //行和列都是从1开始
cout << "[" << i + 1 << "," << e.cols[i] + 1 << "]" << endl;
return; //产生一个解之后结束
}
else //e不是叶子节点
{
for (j = 0; j < 4; j++) //开始检查所有列号
{
i = e.row + 1; //因为e.row是从0开始的
if (isOK(e.cols, i, j))
{
e1.no = count++;
e1.row = i;
e1.cols = e.cols;
e1.cols.push_back(j);
//push_back()函数的用法:函数将一个新的元素加到vector的最后面,位置为当前最后一个元素的下一个元素
qu.push(e1);
Print(e1);
}
}
}
}
}
int main()
{
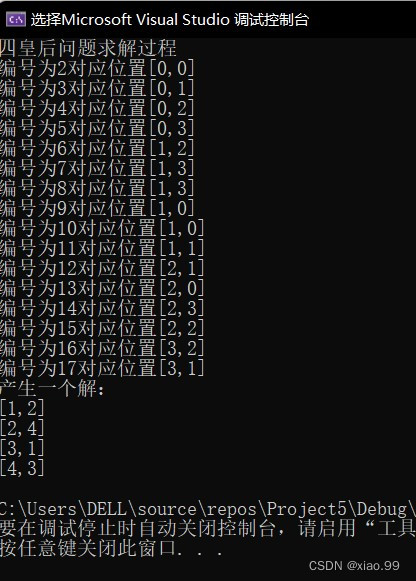
cout << "四皇后问题求解过程" << endl;
queen();
return 0;
}
优先队列的分支限界法
:
row越大越好
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int count = 1;
struct Node
{
int no;
int row;
vector<int>cols;
bool operator<(const Node& s)const
{
return row < s.row;
}
};
int Print(Node e) //输出一个结点的内容
{
if (e.row != -1)
cout << "编号为" << e.no << "对应位置" << "[" << e.row << "," << e.cols[e.row] << "]" << endl;
return 0;
}
int isOK(vector<int> cols, int i, int j) //测试(i,j)这个结点能否放在棋盘上作为皇后
{
for (int k = 0;k < i;k++)
{
if ((cols[k] == j) || abs(cols[k] - j) == abs(k - i))
return 0;
}
return 1;
}
void queen()
{
int i, j, count = 1;
Node e, e1;
priority_queue<Node>qu; //优先队列
e.no = count++;
e.row = -1;
qu.push(e);
while (!qu.empty())
{
e = qu.top();
qu.pop();
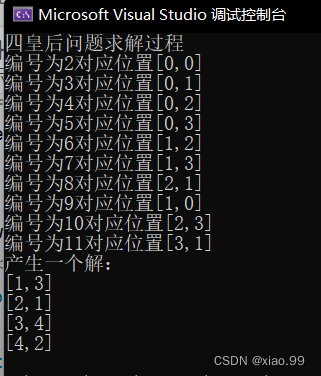
if (e.row == 3)
{
cout << "产生一个解:" << endl;
for (i = 0; i < 4; i++)
cout << "[" << i + 1 << "," << e.cols[i] + 1 << "]" << endl;
return;
}
else
{
for (j = 0; j < 4; j++)
{
i = e.row + 1;
if (isOK(e.cols, i, j))
{
e1.no = count++;
e1.row = i;
e1.cols = e.cols;
e1.cols.push_back(j);
qu.push(e1);
Print(e1);
}
}
}
}
}
int main()
{
cout << "四皇后问题求解过程" << endl;
queen();
return 0;
}
主要是为了自己理解整理了这几种思路,并且更好的理解异同
(1)回溯法只有在所有子节点都被遍历之后才出栈,回溯法的求解目标是找出T中满足约束条件的所有解
(2)分支限界法中每个结点只被访问一次,分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。
关于这道题 ,更适合回溯法
在n
n的国际象棋棋盘上摆下n个后,使所有的后都不能攻击到对方,找出所有符合要求的情况。
n后问题的解空间树是一棵排列树,一旦一种组合是一种解,则解与解之间不存在优劣的分别。直到搜索到叶节点时才能确定出一组解。这时我们用回溯法可以系统地搜索问题的全部解,而且由于解空间树是排列树的特性,代码的编写十分容易,在最坏的情况下,堆栈的深度不会超过n。如果我们采取分支限界法,在解空间树的第一层就会产生n个活结点,如果不考虑剪枝,将在第二层产生n
(n-1)个活节点,如此下去对队列空间的要求太高。n后问题不适合使用分支限界法处理的根源是它需要找处所有解的组合,而不是某种最优解(事实上也没有最优解可言)。形象一点来说,如果让我们自己人工解决n后问题,我们的思路应该是放一个后,看冲不冲突,不冲突的话放下一个,冲突的话改变位置,这样可以只用一个棋盘而且有规律地找到所有符合条件的情况,这正是回溯法的模拟过程。然而分支限界法则可以被这样表述。拿来一个棋盘,摆下一只后;再拿一个棋盘,再摆一只;待到每个棋盘都有一只后以后,每个棋盘又被分解成更多的盘面…,这样,棋盘越来越多,但是由于解和解(包括局部解)之间缺乏因果和限制的联系。棋盘之间并不能根据对方的信息获得什么,这显然是对资源的浪费。
想更多了解他们异同的话,可以去看这个博主写的,我觉着挺好的https://blog.csdn.net/zm1_1zm/article/details/69224626