好久没有更新了,终于把毕业论文初稿给老师了,赶紧继续学习吧!
第一次尝试用markdown
《机器学习实战》第五章:Logistic回归
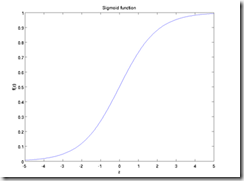
通常,我们需要把输入值转换成类别输出。在只有两个类别的时候,最简单的函数即单位阶跃函数。但是,从0到1的转换瞬间 通常是非常难确定的。所以,Sigmoid函数就可以用来代替单位阶跃函数啦。
Sigmoid函数公式如下:
Γ
(
z
)
=
1
1
+
e
−
z
当x=0时,sigmoid函数值为0.5。
随着x增大,sigmoid值逼近1。
随着x减小,sigmoid值逼近0。
Logistic回归的思想就是,将特征值乘以回归系数,求和后的值输入到sigmoid函数中,进而得到分类结果。
我们将sigmoid函数的输入即为z,则z由以下公式得出:
z
=
w
0
x
0
+
w
1
x
1
+
w
2
x
2
+
…
+
w
n
x
n
其中,
x
表示分类器的输入数据,向量
w
就是Logistic的参数。当然,上式也可以直接写成
z
=
w
T
x
那么,现在问题就变成了,求最优的回归系数
w
为了寻找最佳参数,书中介绍了最优化理论的基础知识。
1.梯度上升法
梯度上升法的基本思想是:要找某个函数的最大值,最好的方法是沿着该函数的梯度方向探寻。
∇
f
(
x
,
y
)
=
⎛
⎝
⎜
∂
f
(
x
,
y
)
∂
x
∂
f
(
x
,
y
)
∂
y
⎞
⎠
⎟
这个梯度
∇
表示沿
x
的方向移动了
∂
f
(
x
,
y
)
∂
x
,沿
y
的方向移动了
∂
f
(
x
,
y
)
∂
y
。
梯度上升算法的迭代公式如下:
w
:
=
w
+
α
∇
w
f
(
w
)
其中,
α
表示移动量的大小,即步长。该迭代一直被执行,直到达到某个停止条件为止。
*****************************************************************************************************************************
更常听到的是梯度下降法。与梯度上升法一样的,但是加法变成减法,即迭代公式变为:
w
:
=
w
−
α
∇
w
f
(
w
)
梯度上升法用来求函数的最大值,梯度下降法用来求函数最小值。
*******************************************************************************************************************************
梯度上升法的伪代码如下:
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
– 每个回归系数初始化为1
– 重复R次:
– 计算整个数据集的梯度
– 使用alpha*gradient更新回归系数的向量
– 返回回归系数
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
代码如下:
from numpy import *
def loadDataSet():
dataMat=[];labelMat=[]
fr=open('testSet.txt')
for line in fr.readlines():
lineArr=line.strip().split()
dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn,classLabels):
dataMatrix=mat(dataMatIn)
#mat()是numpy内的函数,将数组转化为矩阵
labelMat=mat(classLabels).transpose()
#transpose()函数用于矩阵转置
m,n=shape(dataMatrix)
alpha=0.001
#步长
maxCycles=500
weights=ones((n,1))
for k in range(maxCycles):
h=sigmoid(dataMatrix*weights)
#sigmoid函数的分类结果
error=(labelMat-h)
#真实与预测的误差
weights=weights+alpha*dataMatrix.transpose()*error
#用误差乘以数据矩阵的转置表示梯度,此包含一个数学推导
return weights
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr=array(dataMat)
n=shape(dataArr)[0]
#shape求的是大小,[0]表示行数,即数据个数
xcord1=[];ycord1=[]
xcord2=[];ycord2=[]
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
ax.scatter(xcord2,ycord2,s=30,c='green')
#绘制正反类散点图
x=arange(-3.0,3.0,0.1)
y=(-weights[0]-weights[1]*x)/weights[2]
ax.plot(x,y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
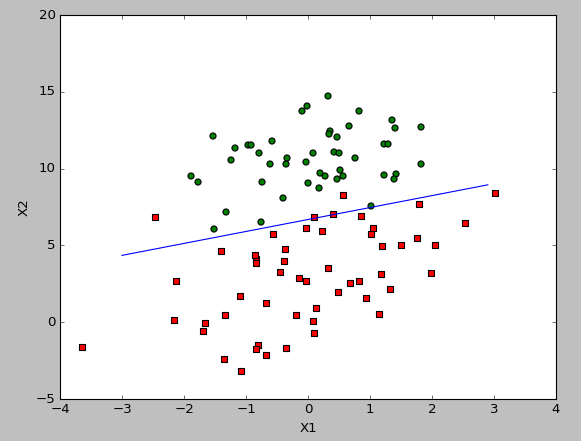
结果如下:
梯度上升算法每次更新回归系数时都需要遍历整个数据集。当样本数量个数巨大或者特征维度特别高时,运算复杂度极高。所以,使用了新方法称为:随机梯度上升算法。可以在新样本到来时对分类器进行增量式更新,因此它是一个
“在线学习算法“
。对应的,一次处理所有数据称为
“批处理”
。
随机梯度上升法的伪代码如下:
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
– 每个回归系数初始化为1
– 对数据集中每个样本
(重复R次)
:
– 计算该样本
(整个数据集)
的梯度
– 使用alpha*gradient更新回归系数的向量
– 返回回归系数
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
def stocGradAscent0(dataMatrix,classLabels):
m,n=shape(dataMatrix)
alpha=0.01
weights=ones(n)
#m表示数据样本的个数
for i in range(m):
h=sigmoid(sum(dataMatrix[i]*weights))
error=classLabels[i]-h
weights=weights+alpha*error*dataMatrix[i]
#此处与原本方法不同的:梯度上升算法是对整个数据集进行操作,所以是以矩阵进行计算
#此函数h和error都是向量
#因为是对每个样本进行操作的
return weights
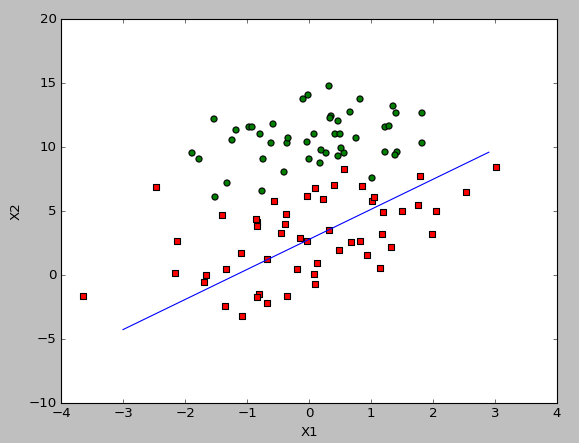
结果如下:
数据集并非是线性可分,该方法受样本的影响较大,容易在每次迭代中发生系数波动。所以,对随机梯度上升算法进行改进。
def stocGradAscent1(dataMatrix,classLabels,numIter=150):
m,n=shape(dataMatrix)
weights=ones(n)
for j in range(numIter):
dataIndex=list(range(m))
for i in range(m):
alpha=4/(1.0+j+i)+0.01
randIndex=int(random.uniform(0,len(dataIndex)))
#uniform(x,y) 方法将随机生成下一个实数,它在[x,y]范围内。
h=sigmoid(sum(dataMatrix[randIndex]*weights))
error=classLabels[randIndex]-h
weights=weights+alpha*error*dataMatrix[randIndex]
del (dataIndex[randIndex])
return weights
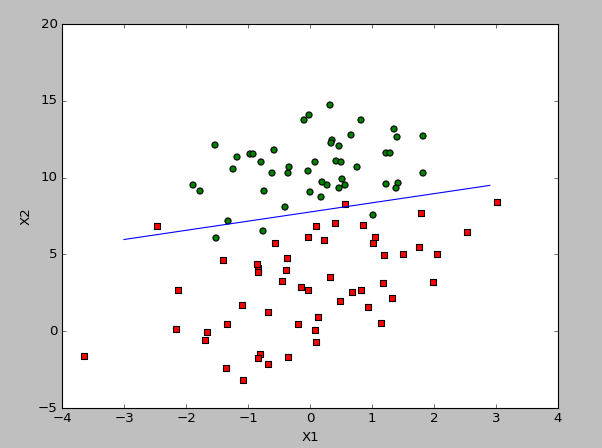
此处,alpha在每次迭代每个样本时都进行调整。alpha会随着迭代次数不断减少,但不会减小到0。随机选取样本的方法可以减少周期的波动。
此处将dataIndex从range外改成list型。
实例
分类函数:
def classifyVector(inX,weights):
prob=sigmoid(sum(inX*weights))
if prob>0.5:
return 1.0
else:
return 0.0测试过程:
def coliTest():
frTrain=open('horseColicTraining.txt')
frTest=open('horseColicTraining.txt')
trainingSet=[]
trainingLabels=[]
for line in frTrain.readlines():
currLine=line.strip().split('\t')
lineArr=[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights=stocGradAscent1(array(trainingSet),trainingLabels,500)
errorCount=0
numTestVec=0.0
for line in frTest.readlines():
numTestVec+=1.0
currLine=line.strip().split('\t')
lineArr=[]
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr),trainWeights))!= round(float(currLine[21])):
errorCount+=1
errorRate=(float(errorCount)/numTestVec)
print('the error rate of this test is:%f' %errorRate)
return errorRate
def multiTest():
numTest=10
errorSum=0.0
for k in range(numTest):
errorSum+=coliTest()
print('after %d iterations the average error rate is :%f' %(numTest,errorSum/float(numTest)))
Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数,求解过程可由优化算法来完成。在最优化算法中,最常用的是梯度上升算法。