On Tchebycheff Decomposition Approaches for
Multiobjective Evolutionary Optimization
Digital Object Identifier 10.1109/TEVC.2017.2704118
摘要:
Tchebycheff分解是一种极广泛使用的分解方法,其能将一个多目标优化问题转化为一组标量优化子问题。然而,在Tchebycheff分解中,子目标函数的几何属性还没有被详尽地研究。本文通过对方向向量进行
l
p
l
p
-范式约束提出了一种Tchebycheff分解方法,其中,子目标函数具有明确的几何属性。尤其,对方向向量进行
l
2
l
2
-范式约束的Tchebycheff分解作为例子被用于说明其优越性。同时,一个新的一元
R
2
R
2
指标被引入来近似超体积度量(Hyper-volume metric)及证明提出的Tchebycheff分解的有效性。最终,一个基于使用
l
2
l
2
-范式约束的Tchebycheff分解的多目标优化算法和一个新的种群更新策略被提出来解决多目标优化问题。在基准测试集及现实世界的多目标优化问题上的实验结果表明,相比其他主流多目标优化算法,提出的算法能够获得高质量的解。
索引词
—Tchebycheff分解,基于分解的多目标优化算法,种群更新策略,最大适应值改善,
R
2
R
2
指标
I. 引言
一个多目标问题(Multi-objective problem,MOP)【1,2】可以用公式描述为:
min
F
(
x
)
=
(
f
1
(
x
)
,
f
2
(
x
)
,
.
.
.
,
f
m
(
x
)
)
min
F
(
x
)
=
(
f
1
(
x
)
,
f
2
(
x
)
,
.
.
.
,
f
m
(
x
)
)
(1)
s
u
b
j
e
c
t
t
o
:
x
∈
Ω
s
u
b
j
e
c
t
t
o
:
x
∈
Ω
其中,
x
x
为一个决策变量向量,
为决策空间,
F
(
x
)
:
Ω
→
R
m
F
(
x
)
:
Ω
→
R
m
为
m
m
个目标函数的一个
-维向量。
令
x
a
x
a
和
x
b
x
b
表示两个决策向量,
x
a
x
a
支配
x
b
x
b
(表示为
x
a
≺
x
b
x
a
≺
x
b
),当且仅当
∀
i
∈
{
1
,
.
.
.
,
m
}
,
f
i
(
x
a
)
≤
f
i
(
x
b
)
∀
i
∈
{
1
,
.
.
.
,
m
}
,
f
i
(
x
a
)
≤
f
i
(
x
b
)
及
F
(
x
a
)
≠
F
(
x
b
)
F
(
x
a
)
≠
F
(
x
b
)
。一个解
x
∗
∈
Ω
x
∗
∈
Ω
如果不被其他任何解支配,则被称为是Pareto最优的。所有的Pareto最优解组成了Pareto最优集(Pareto optimal set,PS),即,
P
S
=
{
x
∗
|
∄
x
∈
Ω
,
x
≺
x
∗
}
P
S
=
{
x
∗
|
∄
x
∈
Ω
,
x
≺
x
∗
}
。相应的最优目标向量集称为Pareto最优前沿(Pareto optimal front,PF),即,
P
F
=
{
F
(
x
)
|
x
∈
P
S
}
P
F
=
{
F
(
x
)
|
x
∈
P
S
}
。
基于分解的多目标优化算法(MOEA/D)已被认为是一种非常有效的估计
P
F
P
F
的方法【3-14】。分解方法是MOEA/D的关键组成。Tchebycheff分解是一种最为广泛使用的分解方法。然而,使用均匀权重向量的Tchebycheff分解所获得的解通常并不是均匀分布的【5-9】。广义分解【5-7】和改进的Tchebycheff分解【9,10】被提出以解决此问题,但在这些Tchebycheff分解方法中的子目标函数的几何属性还没有被详尽地研究。
本文提出一种对方向向量进行
l
p
l
p
-范式约束的Tchebycheff分解方法(
p
p
-Tch),其中,子目标函数有明确的几何属性。对
-Tch和其他Tchebycheff分解方法的关系进行了研究。不同的
p
p
值对MOEA/D的子问题施加了不同的竞争压力。使用
-范式约束(2-Tch)的Tchebycheff分解被作为例子来说明所提出的分解方法的优点。指标
R
2
t
c
h
2
R
2
2
t
c
h
,一种基于2-Tch的
R
2
R
2
指标【15】的变体,也被引入以近似超体积度量来证实提出的Tchebycheff分解的有效性。
MOEA/D框架中使用了2-Tch及一个新的种群更新策略。在大多数的MOEA/D变体(比如,【4,16-18】)中,进化种群的更新是基于一种局部随机策略。在【19】中,一种基于最小适应值的全局策略被提出。然而,上述策略都是被设计用来优化某些子问题的性能,而不是所有子问题。为解决此问题,本文引入了一种基于最大适应值改善的全局种群更新策略来优化所有子问题的总体性能。最终的算法,MOEA/D-2TCHMFI(基于2-Tch和最大适应值提升的种群更新策略的MOEA/D),在多种基准测试集和现实世界的多目标优化问题上进行了测试。实验结果表明,相比其他多目标优化算法,MOEA/D-2TCHMFI能够得到高质量的解。
在本文的其余部分,第II节回顾了两种密切相关的Tchebycheff分解方法。所提出的对方向向量进行
l
p
l
p
-范式约束的Tchebycheff分解方法和分解的广义形式在第III节引入。第IV节提出了基于最大适应值改善的种群更新策略。最终的MOEA/D-2TCHMFI算法在第V节被描述。第VI节定义了提出的一元指标
R
2
t
c
h
2
R
2
2
t
c
h
。第VII节展示了MOEA/D-2TCHMFI和其他先进多目标优化算法的比较结果。最后,第VIII节对本工作进行了总结。
II. 两种关系密切的Tchebycheff分解方法
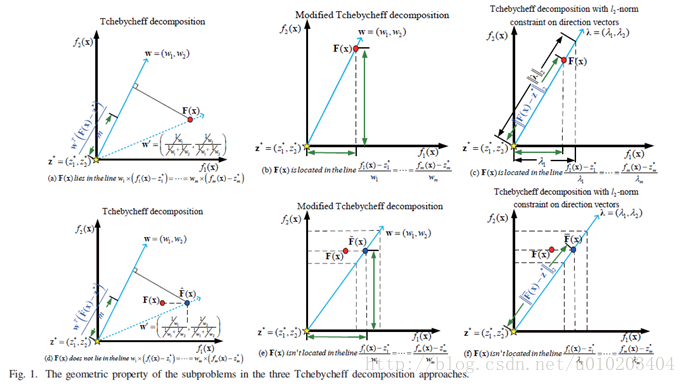
在本节,我们回顾了两种关系密切的Tchebycheff分解方法,即,传统Tchebycheff分解【20】和改进Tchebycheff分解【10】。在这两种Tchebycheff分解方法中的子问题目标函数的几何属性被详细研究。
A. 传统Tchebycheff分解
传统Tchebycheff分解将一个MOP分解成一组标量优化子问题,每一个的定义如下:
min
x
∈
Ω
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
1
≤
i
≤
m
{
w
i
(
f
i
(
x
)
−
z
∗
)
}
min
x
∈
Ω
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
1
≤
i
≤
m
{
w
i
(
f
i
(
x
)
−
z
∗
)
}
(2)
其中,
w
i
=
(
w
1
,
.
.
.
,
w
m
)
w
i
=
(
w
1
,
.
.
.
,
w
m
)
满足
∑
m
i
=
1
w
i
=
1
∑
i
=
1
m
w
i
=
1
及
w
i
≥
0
w
i
≥
0
,为一个子问题的权重向量,
z
∗
=
(
z
∗
1
,
z
∗
2
,
.
.
.
,
z
∗
m
)
z
∗
=
(
z
1
∗
,
z
2
∗
,
.
.
.
,
z
m
∗
)
满足
z
∗
i
<
min
{
f
i
(
x
)
|
x
∈
Ω
}
z
i
∗
<
min
{
f
i
(
x
)
|
x
∈
Ω
}
,为一理想目标向量。
传统Tchebycheff分解中的子问题目标函数的几何属性还没有被研究。据我们所知,本工作首次研究了Tchebycheff分解中的子问题目标函数的几何属性。
命题 2.1:
令
z
∗
=
(
z
∗
1
,
.
.
.
,
z
∗
m
)
z
∗
=
(
z
1
∗
,
.
.
.
,
z
m
∗
)
为(1)的一个理想目标向量,
w
=
(
w
1
,
.
.
.
,
w
m
)
w
=
(
w
1
,
.
.
.
,
w
m
)
为正权重向量。若一个给定的目标向量
F
(
x
)
=
(
f
1
(
X
)
,
.
.
.
,
F
m
(
x
)
)
F
(
x
)
=
(
f
1
(
X
)
,
.
.
.
,
F
m
(
x
)
)
位于直线
L
1
:
w
1
(
f
1
(
x
)
−
z
∗
1
)
=
.
.
.
=
w
m
(
f
m
(
x
)
−
z
∗
m
)
L
1
:
w
1
(
f
1
(
x
)
−
z
1
∗
)
=
.
.
.
=
w
m
(
f
m
(
x
)
−
z
m
∗
)
如图1(a)所示。那么,
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
w
T
(
F
(
x
)
−
z
∗
)
m
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
w
T
(
F
(
x
)
−
z
∗
)
m
(3)
证明
由于
F
(
x
)
F
(
x
)
位于直线
L
1
L
1
,我们得到
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
=
=
(
2
)
max
1
≤
i
≤
m
{
w
i
(
f
i
(
x
)
−
z
∗
i
)
}
=
=
=
L
1
w
1
(
f
1
(
x
)
−
z
∗
1
)
=
.
.
.
=
w
m
(
f
m
(
x
)
−
z
∗
m
)
=
∑
m
i
=
1
w
i
(
f
i
(
x
)
−
z
∗
i
)
m
=
w
T
(
F
(
x
)
−
z
∗
)
m
■
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
===
(
2
)
max
1
≤
i
≤
m
{
w
i
(
f
i
(
x
)
−
z
i
∗
)
}
===
L
1
w
1
(
f
1
(
x
)
−
z
1
∗
)
=
.
.
.
=
w
m
(
f
m
(
x
)
−
z
m
∗
)
=
∑
i
=
1
m
w
i
(
f
i
(
x
)
−
z
i
∗
)
m
=
w
T
(
F
(
x
)
−
z
∗
)
m
◼
公式(3)用于说明
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
的几何属性,而不是找到
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
的最优解,即,
min
x
∈
Ω
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
min
x
∈
Ω
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
。以
F
(
x
)
=
(
1
/
2
,
1
/
4
)
F
(
x
)
=
(
1
/
2
,
1
/
4
)
,
z
∗
=
(
0
,
0
)
z
∗
=
(
0
,
0
)
及
w
=
(
1
/
3
,
2
/
3
)
w
=
(
1
/
3
,
2
/
3
)
为例,如图1(a)所示,我们可以使用等式(3)来解释子问题适应值
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
,
w
w
,与
的关系。式(3)(即
w
T
(
F
(
x
)
−
z
∗
)
/
m
w
T
(
F
(
x
)
−
z
∗
)
/
m
)给出了
l
1
l
1
-范式的加权形式,为
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
的对偶式【21,pp. 637】。
F
(
x
)
F
(
x
)
不位于
L
1
L
1
的情形可以如下命题描述。
命题 2.2:
令
z
∗
=
(
z
∗
1
,
.
.
.
,
z
∗
m
)
z
∗
=
(
z
1
∗
,
.
.
.
,
z
m
∗
)
为一个(1)的理想目标向量,
w
=
(
w
1
,
.
.
.
,
w
m
)
w
=
(
w
1
,
.
.
.
,
w
m
)
为一个正的权重向量。给定一个目标向量
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
,
F
^
(
x
)
=
(
f
^
1
(
x
)
,
.
.
.
,
f
^
m
(
x
)
)
F
^
(
x
)
=
(
f
^
1
(
x
)
,
.
.
.
,
f
^
m
(
x
)
)
可以如下构建:1)
F
^
(
x
)
F
^
(
x
)
与
F
(
x
)
F
(
x
)
有相同的子问题适应值,即,
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
g
t
c
h
(
F
^
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
g
t
c
h
(
F
^
(
x
)
|
w
,
z
∗
)
;2)
F
^
(
x
)
F
^
(
x
)
位于图1(d)所示的直线
L
1
L
1
。那么,如下等式可以满足:
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
w
T
(
F
^
(
x
)
−
z
∗
)
m
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
w
T
(
F
^
(
x
)
−
z
∗
)
m
(4)
证明
由
F
^
(
x
)
F
^
(
x
)
的构建,我们得到
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
=
=
1
)
=
=
=
=
=
=
=
2
)
F
^
(
x
)
is in
L
1
w
T
(
F
^
(
x
)
−
z
∗
)
m
■
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
===
1
)
=======
2
)
F
^
(
x
)
is in
L
1
w
T
(
F
^
(
x
)
−
z
∗
)
m
◼
备注
给定目标向量
F
(
x
)
F
(
x
)
,
F
^
(
x
)
=
(
f
^
1
(
x
)
,
.
.
.
,
f
^
m
(
x
)
)
F
^
(
x
)
=
(
f
^
1
(
x
)
,
.
.
.
,
f
^
m
(
x
)
)
实际上是
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
的等值线与
L
1
L
1
在目标空间的交点,如图1(d)所示,并且
f
^
i
(
x
)
=
z
∗
i
+
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
w
i
,
i
=
1
,
.
.
.
,
m
f
^
i
(
x
)
=
z
i
∗
+
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
w
i
,
i
=
1
,
.
.
.
,
m
由于这样的事实:
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
=
=
1
)
g
t
c
h
(
F
^
(
x
)
|
w
,
z
∗
)
=
=
=
2
)
w
1
(
f
^
1
(
x
)
−
z
∗
1
)
=
.
.
.
=
w
m
(
f
^
m
(
x
)
−
z
∗
m
)
■
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
===
1
)
g
t
c
h
(
F
^
(
x
)
|
w
,
z
∗
)
===
2
)
w
1
(
f
^
1
(
x
)
−
z
1
∗
)
=
.
.
.
=
w
m
(
f
^
m
(
x
)
−
z
m
∗
)
◼
以
F
(
x
)
=
(
1
,
1
)
F
(
x
)
=
(
1
,
1
)
,
z
∗
=
(
0
,
0
)
z
∗
=
(
0
,
0
)
,及
w
=
(
1
/
3
,
2
/
3
)
w
=
(
1
/
3
,
2
/
3
)
为例,我们能得到:
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
{
1
3
(
1
−
0
)
,
2
3
(
1
−
0
)
}
=
2
/
3
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
{
1
3
(
1
−
0
)
,
2
3
(
1
−
0
)
}
=
2
/
3
,
f
^
1
(
x
)
=
z
∗
1
+
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
w
1
=
0
+
2
/
3
1
/
3
=
2
f
^
1
(
x
)
=
z
1
∗
+
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
w
1
=
0
+
2
/
3
1
/
3
=
2
,
f
^
2
(
x
)
=
z
∗
2
+
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
w
2
=
0
+
2
/
3
2
/
3
=
1
f
^
2
(
x
)
=
z
2
∗
+
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
w
2
=
0
+
2
/
3
2
/
3
=
1
.
B. 改进Tchebycheff分解
为处理最优解与相应的子问题权重向量之间的非线性关系【5-8,22-24】,研究【10】提出了改进Tchebycheff分解。并没有与(2)中的
w
i
w
i
相乘,改进Tchebycheff分解通过用
f
i
(
x
)
−
z
∗
i
f
i
(
x
)
−
z
i
∗
除以
w
i
w
i
来构建子问题,如下:
min
x
∈
Ω
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
∗
i
w
i
}
min
x
∈
Ω
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
i
∗
w
i
}
(5)
对改进Tchebycheff分解中的一个子问题目标函数的几何属性的研究如下。
命题 2.3:
令
z
∗
=
(
z
∗
1
,
.
.
.
,
z
∗
m
)
z
∗
=
(
z
1
∗
,
.
.
.
,
z
m
∗
)
为(1)中的一理想目标向量,
w
=
(
w
1
,
.
.
.
,
w
m
)
w
=
(
w
1
,
.
.
.
,
w
m
)
为一正的权重向量。若一给定的目标向量
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
位于直线
L
2
:
f
1
(
x
)
−
z
∗
1
w
1
=
.
.
.
=
f
m
(
x
)
−
z
∗
m
w
m
L
2
:
f
1
(
x
)
−
z
1
∗
w
1
=
.
.
.
=
f
m
(
x
)
−
z
m
∗
w
m
如图1(b)所示。那么,
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
∥
F
(
x
)
−
z
∗
∥
1
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
‖
F
(
x
)
−
z
∗
‖
1
(6)
证明
由于
F
(
x
)
F
(
x
)
在
L
2
L
2
上,我们可以得出,
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
=
=
(
5
)
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
∗
i
w
i
}
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
===
(
5
)
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
i
∗
w
i
}
=
=
=
L
2
f
1
(
x
)
−
z
∗
1
w
1
=
.
.
.
=
f
m
(
x
)
−
z
∗
m
w
m
===
L
2
f
1
(
x
)
−
z
1
∗
w
1
=
.
.
.
=
f
m
(
x
)
−
z
m
∗
w
m
=
∑
m
i
=
1
(
f
i
(
x
)
−
z
∗
i
)
∑
m
i
=
1
w
i
=
∥
F
(
x
)
−
z
∗
∥
1
■
=
∑
i
=
1
m
(
f
i
(
x
)
−
z
i
∗
)
∑
i
=
1
m
w
i
=
‖
F
(
x
)
−
z
∗
‖
1
◼
以
F
(
x
)
=
(
1
/
4
,
2
/
4
)
F
(
x
)
=
(
1
/
4
,
2
/
4
)
,
z
∗
=
(
0
,
0
)
z
∗
=
(
0
,
0
)
,及
w
=
(
1
/
3
,
2
/
3
)
w
=
(
1
/
3
,
2
/
3
)
为例,式(6)可以如下计算:
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
{
f
1
(
x
)
−
z
∗
1
w
1
,
f
2
(
x
)
−
z
∗
2
w
2
}
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
{
f
1
(
x
)
−
z
1
∗
w
1
,
f
2
(
x
)
−
z
2
∗
w
2
}
=
max
{
1
/
4
−
0
1
/
3
,
2
/
4
−
0
2
/
3
}
=
3
4
=
∥
F
(
x
)
−
z
∗
∥
1
=
max
{
1
/
4
−
0
1
/
3
,
2
/
4
−
0
2
/
3
}
=
3
4
=
‖
F
(
x
)
−
z
∗
‖
1
当
F
(
x
)
F
(
x
)
不在
L
2
L
2
时,以下命题描述了
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
的几何属性。
命题 2.4:
令
z
∗
=
(
z
∗
1
,
.
.
.
,
z
∗
m
)
z
∗
=
(
z
1
∗
,
.
.
.
,
z
m
∗
)
为(1)中的一理想目标向量,
w
=
(
w
1
,
.
.
.
,
w
m
)
w
=
(
w
1
,
.
.
.
,
w
m
)
为一正的权重向量。给定一目标向量
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
,可以由满足以下两个约束生成
F
~
(
x
)
=
(
f
~
1
(
x
)
,
.
.
.
,
f
~
m
(
x
)
)
F
~
(
x
)
=
(
f
~
1
(
x
)
,
.
.
.
,
f
~
m
(
x
)
)
:1)
f
~
(
x
)
f
~
(
x
)
和
F
(
x
)
F
(
x
)
位于同一等值线上,即,
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
g
m
t
c
h
(
F
~
(
x
)
|
w
,
z
∗
)
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
g
m
t
c
h
(
F
~
(
x
)
|
w
,
z
∗
)
;及2)
f
~
(
x
)
f
~
(
x
)
位于直线
L
2
L
2
上,如图1(e)所示。那么,
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
∥
∥
F
~
(
x
)
−
z
∗
∥
∥
1
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
‖
F
~
(
x
)
−
z
∗
‖
1
(7)
证明
据
F
~
(
x
)
F
~
(
x
)
的情况,我们得到
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
=
=
=
1
)
g
m
t
c
h
(
F
~
(
x
)
|
w
,
z
∗
)
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
===
1
)
g
m
t
c
h
(
F
~
(
x
)
|
w
,
z
∗
)
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
2
)
F
~
(
x
)
is in
L
2
{Proposition 2.3}
∥
∥
F
~
(
x
)
−
z
∗
∥
∥
1
■
====================
2
)
F
~
(
x
)
is in
L
2
{Proposition 2.3}
‖
F
~
(
x
)
−
z
∗
‖
1
◼
备注
在几何中,
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
等同于
F
~
(
x
)
−
z
∗
F
~
(
x
)
−
z
∗
的
l
1
l
1
-范式,如图1(e)所示。
F
~
(
x
)
F
~
(
x
)
为直线
L
2
L
2
与
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
的等值线的交点,如图1(e)所示。
F
~
(
x
)
=
(
f
~
1
(
x
)
,
.
.
.
,
f
~
m
(
x
)
)
=
z
∗
+
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
⋅
w
F
~
(
x
)
=
(
f
~
1
(
x
)
,
.
.
.
,
f
~
m
(
x
)
)
=
z
∗
+
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
⋅
w
由于
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
=
=
1
)
g
m
t
c
h
(
F
~
(
x
)
|
w
,
z
∗
)
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
===
1
)
g
m
t
c
h
(
F
~
(
x
)
|
w
,
z
∗
)
=
=
=
=
=
2
)
L
2
f
~
1
(
x
)
−
z
∗
1
w
1
=
.
.
.
=
f
~
m
(
x
)
−
z
∗
m
w
m
■
=====
2
)
L
2
f
~
1
(
x
)
−
z
1
∗
w
1
=
.
.
.
=
f
~
m
(
x
)
−
z
m
∗
w
m
◼
例如,给定
F
(
x
)
=
(
0.5
,
2
)
F
(
x
)
=
(
0.5
,
2
)
,
z
∗
=
(
0
,
0
)
z
∗
=
(
0
,
0
)
,及
w
=
(
1
/
3.2
/
3
)
w
=
(
1
/
3.2
/
3
)
,我们可以计算
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
{
0.5
−
0
1
/
3
,
2
−
0
2
/
3
}
=
3
,
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
=
max
{
0.5
−
0
1
/
3
,
2
−
0
2
/
3
}
=
3
,
f
~
1
(
x
)
=
z
∗
1
+
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
⋅
w
1
=
0
+
3
⋅
1
/
3
=
1
,
f
~
1
(
x
)
=
z
1
∗
+
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
⋅
w
1
=
0
+
3
⋅
1
/
3
=
1
,
f
~
2
(
x
)
=
z
∗
2
+
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
⋅
w
2
=
0
+
3
⋅
2
/
3
=
2.
f
~
2
(
x
)
=
z
2
∗
+
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
⋅
w
2
=
0
+
3
⋅
2
/
3
=
2.
III. 提出的对方向向量进行
l
p
l
p
-范式约束的Tchebycheff分解
通过对改进Tchebycheff分解进行拓展,本文提出一种新的对方向向量进行
l
p
l
p
-范式约束的Tchebycheff分解方法,简称为
p
p
-Tch。在
-Tch中,每个子问题的构建基于一个满足
∥
λ
∥
p
=
1
‖
λ
‖
p
=
1
的方向向量
λ
λ
,而不是改进Tchebycheff分解中使用的满足
∥
w
∥
1
=
∑
m
i
=
1
w
i
=
1
‖
w
‖
1
=
∑
i
=
1
m
w
i
=
1
的权重向量
w
w
,即,
(8)
其中,
λ
=
(
λ
1
,
.
.
.
,
λ
m
)
λ
=
(
λ
1
,
.
.
.
,
λ
m
)
满足
∥
λ
∥
p
=
1
‖
λ
‖
p
=
1
及
λ
1
,
.
.
.
,
λ
m
>
0
λ
1
,
.
.
.
,
λ
m
>
0
。注意,改进Tchebycheff分解(5)是
p
=
1
p
=
1
时的
p
p
-Tch的一种特殊形式,近似于Chebyshev近似问题【21,pp. 293】,是
-Tch(8)的一个同等问题,可用公式描述为:
min
x
∈
Ω
t
min
x
∈
Ω
t
s
.
t
.
f
i
(
x
)
−
z
∗
i
λ
i
≤
t
,
i
=
1
,
.
.
.
,
m
s
.
t
.
f
i
(
x
)
−
z
i
∗
λ
i
≤
t
,
i
=
1
,
.
.
.
,
m
A.
p
p
-Tch中的子问题目标函数的几何属性
命题 3.1:
令
为(1)的一个理想目标向量,方向向量
λ
λ
为一正向量且满足
∥
λ
∥
p
=
1
‖
λ
‖
p
=
1
。若一给定的目标向量
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
位于直线
L
3
:
f
1
(
x
)
−
z
∗
1
λ
1
=
.
.
.
=
f
m
(
x
)
−
z
∗
m
λ
m
.
L
3
:
f
1
(
x
)
−
z
1
∗
λ
1
=
.
.
.
=
f
m
(
x
)
−
z
m
∗
λ
m
.
那么
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
∥
F
(
x
)
−
z
∗
∥
p
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
‖
F
(
x
)
−
z
∗
‖
p
(9)
证明
由于
f
i
(
x
)
−
z
∗
i
≥
0
f
i
(
x
)
−
z
i
∗
≥
0
并且对于
∀
i
∈
{
1
,
2
,
.
.
.
,
m
}
∀
i
∈
{
1
,
2
,
.
.
.
,
m
}
有
λ
i
>
0
λ
i
>
0
,
k
(
x
)
≜
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
=
=
(
8
)
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
∗
i
λ
i
}
k
(
x
)
≜
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
===
(
8
)
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
i
∗
λ
i
}
=
=
=
L
3
f
1
(
x
)
−
z
∗
1
λ
1
=
.
.
.
=
f
m
(
x
)
−
z
∗
m
λ
m
≥
0
===
L
3
f
1
(
x
)
−
z
1
∗
λ
1
=
.
.
.
=
f
m
(
x
)
−
z
m
∗
λ
m
≥
0
(10)
由于对于
i
=
1
,
.
.
.
,
m
i
=
1
,
.
.
.
,
m
有
f
i
(
x
)
−
z
∗
i
=
λ
i
⋅
k
(
x
)
f
i
(
x
)
−
z
i
∗
=
λ
i
⋅
k
(
x
)
,且
F
(
x
)
−
z
∗
=
k
(
x
)
⋅
λ
F
(
x
)
−
z
∗
=
k
(
x
)
⋅
λ
,我们有
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
k
(
x
)
=
=
=
=
=
∥
λ
∥
p
=
1
k
(
x
)
⋅
∥
λ
∥
p
=
=
=
=
=
=
=
=
k
(
x
)
≥
0
(
10
)
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
k
(
x
)
=====
‖
λ
‖
p
=
1
k
(
x
)
⋅
‖
λ
‖
p
========
k
(
x
)
≥
0
(
10
)
∥
k
(
x
)
⋅
λ
∥
p
=
=
=
=
=
=
=
=
=
=
=
k
(
x
)
⋅
=
F
(
x
)
−
z
∗
∥
F
(
x
)
−
z
∗
∥
p
‖
k
(
x
)
⋅
λ
‖
p
===========
k
(
x
)
⋅
=
F
(
x
)
−
z
∗
‖
F
(
x
)
−
z
∗
‖
p
(11)
■
◼
以
p
=
2
p
=
2
,
F
(
x
)
=
(
1
,
2
)
F
(
x
)
=
(
1
,
2
)
,
λ
=
(
1
/
5
–
√
,
2
/
5
–
√
)
λ
=
(
1
/
5
,
2
/
5
)
,及
z
∗
=
(
0
,
0
)
z
∗
=
(
0
,
0
)
为例,我们能得到
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
max
{
f
1
(
x
)
−
z
∗
1
λ
1
,
f
2
(
x
)
−
z
∗
2
λ
2
}
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
max
{
f
1
(
x
)
−
z
1
∗
λ
1
,
f
2
(
x
)
−
z
2
∗
λ
2
}
=
max
{
1
−
0
1
/
5
–
√
,
2
−
0
2
/
5
–
√
}
=
5
–
√
=
∥
F
(
x
)
−
z
∗
∥
2
=
max
{
1
−
0
1
/
5
,
2
−
0
2
/
5
}
=
5
=
‖
F
(
x
)
−
z
∗
‖
2
命题3.1描述的情形在
p
=
2
p
=
2
时可以用图1(c)说明。如图所示,
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
为
p
=
2
p
=
2
时的
z
∗
z
∗
到
F
(
x
)
F
(
x
)
的欧氏距离。
F
(
x
)
F
(
x
)
不位于
L
3
L
3
的情形可以用如下命题描述。
命题 3.2:
,令
z
∗
=
(
z
∗
1
,
.
.
.
,
z
∗
m
)
z
∗
=
(
z
1
∗
,
.
.
.
,
z
m
∗
)
为(1)的一理想目标向量,方向向量
λ
λ
为满足
∥
λ
∥
p
=
1
‖
λ
‖
p
=
1
的方向向量。给定一目标向量
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
F
(
x
)
=
(
f
1
(
x
)
,
.
.
.
,
f
m
(
x
)
)
,
F
¯
(
x
)
=
(
f
¯
1
(
x
)
,
.
.
.
,
f
¯
m
(
x
)
)
F
¯
(
x
)
=
(
f
¯
1
(
x
)
,
.
.
.
,
f
¯
m
(
x
)
)
满足两个约束:1)
F
¯
(
x
)
F
¯
(
x
)
与
F
(
x
)
F
(
x
)
具有相同的适应值,即,
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
g
p
t
c
h
(
F
¯
(
x
)
|
λ
,
z
∗
)
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
g
p
t
c
h
(
F
¯
(
x
)
|
λ
,
z
∗
)
;2)
F
¯
(
x
)
F
¯
(
x
)
位于直线
L
3
L
3
上,如图1(f)所示。那么,
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
∥
∥
F
¯
(
x
)
−
z
∗
∥
∥
p
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
‖
F
¯
(
x
)
−
z
∗
‖
p
(12)
证明
由
F
¯
(
x
)
F
¯
(
x
)
的组成,我们能得到
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
=
=
1
)
g
p
t
c
h
(
F
¯
(
x
)
|
λ
,
z
∗
)
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
2
)
F
¯
(
x
)
is in
L
3
P
r
o
p
o
s
i
t
i
o
n
3.1
∥
∥
F
¯
(
x
)
−
z
∗
∥
∥
p
■
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
===
1
)
g
p
t
c
h
(
F
¯
(
x
)
|
λ
,
z
∗
)
==================
2
)
F
¯
(
x
)
is in
L
3
P
r
o
p
o
s
i
t
i
o
n
3.1
‖
F
¯
(
x
)
−
z
∗
‖
p
◼
根据
F
¯
(
x
)
F
¯
(
x
)
的两个约束,我们能得到
F
¯
(
x
)
=
(
f
¯
1
(
x
)
,
.
.
.
,
f
¯
m
(
x
)
)
=
z
∗
+
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
⋅
λ
F
¯
(
x
)
=
(
f
¯
1
(
x
)
,
.
.
.
,
f
¯
m
(
x
)
)
=
z
∗
+
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
⋅
λ
例如,给定
p
=
2
p
=
2
,
F
(
x
)
=
(
0.5
,
2
)
F
(
x
)
=
(
0.5
,
2
)
,
λ
=
(
1
/
5
–
√
,
2
/
5
–
√
)
λ
=
(
1
/
5
,
2
/
5
)
,及
z
∗
=
(
0
,
0
)
z
∗
=
(
0
,
0
)
,我们可以计算
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
max
{
0.5
−
0
1
/
5
–
√
,
2
−
0
2
/
5
–
√
}
=
5
–
√
,
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
max
{
0.5
−
0
1
/
5
,
2
−
0
2
/
5
}
=
5
,
f
¯
1
(
x
)
=
z
∗
1
+
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
⋅
λ
1
=
0
+
5
–
√
⋅
1
/
5
–
√
=
1
,
f
¯
1
(
x
)
=
z
1
∗
+
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
⋅
λ
1
=
0
+
5
⋅
1
/
5
=
1
,
f
¯
2
(
x
)
=
z
∗
2
+
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
⋅
λ
2
=
0
+
5
–
√
⋅
2
/
5
–
√
=
2.
f
¯
2
(
x
)
=
z
2
∗
+
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
⋅
λ
2
=
0
+
5
⋅
2
/
5
=
2.
B. 改进Tchebycheff分解与
p
p
-Tch的关系
改进Tchebycheff分解与
-Tch在构造子问题时具有相似之处,即,
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
=
=
=
=
=
=
λ
=
w
∥
w
∥
p
g
p
t
c
h
(
F
(
x
)
|
w
∥
w
∥
p
,
z
∗
)
g
p
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
======
λ
=
w
‖
w
‖
p
g
p
t
c
h
(
F
(
x
)
|
w
‖
w
‖
p
,
z
∗
)
=
=
=
(
8
)
max
1
≤
i
≤
m
⎧
⎩
⎨
f
i
(
x
)
−
z
∗
i
w
i
∥
w
∥
p
⎫
⎭
⎬
=
∥
w
∥
p
⋅
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
∗
i
w
i
}
===
(
8
)
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
i
∗
w
i
‖
w
‖
p
}
=
‖
w
‖
p
⋅
max
1
≤
i
≤
m
{
f
i
(
x
)
−
z
i
∗
w
i
}
=
=
=
(
5
)
∥
w
∥
p
⋅
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
===
(
5
)
‖
w
‖
p
⋅
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
(13)
其中,
p
p
-Tch与改进Tchebycheff分解的不同之处在于产生权重因子
的方法。
式(13)可以被一般化。更具体来说,若
g
(
F
(
x
)
|
w
,
z
∗
)
g
(
F
(
x
)
|
w
,
z
∗
)
表示一个分解方法(如,传统Tchebycheff分解,改进Tchebycheff分解,加权和方法【20】或PBI方法【3】)的子问题,那么,那么一个泛化的子问题目标函数可以定义为
c
(
w
)
⋅
g
(
F
(
x
)
|
w
,
z
∗
)
c
(
w
)
⋅
g
(
F
(
x
)
|
w
,
z
∗
)
,其中,
c
(
w
)
c
(
w
)
为只依赖于权重向量
w
w
的系数,且对于任何
有
c
(
w
)
>
0
c
(
w
)
>
0
。在
p
p
-Tch中,
。
C. 提出的泛化子问题的优点
泛化子问题相比于原始子问题的优点在于泛化能够调整子问题在竞争中的重要性/权重,这对应其被后代解更新的几率。
1) 通过划分可行目标空间调节子问题的重要性:
c
(
w
)
c
(
w
)
能被看作为子问题的权重/重要性。子问题偏好区域的定义可以介绍如下:
Υ
i
=
{
F
(
x
)
|
x
∈
Ω
,
arg
min
1
≤
i
≤
N
{
c
(
w
j
)
⋅
g
(
F
(
x
)
|
w
j
,
z
∗
)
}
=
i
}
Υ
i
=
{
F
(
x
)
|
x
∈
Ω
,
arg
min
1
≤
i
≤
N
{
c
(
w
j
)
⋅
g
(
F
(
x
)
|
w
j
,
z
∗
)
}
=
i
}
(14)
其中,
N
N
为子问题的个数。在
中,
c
(
w
i
)
⋅
g
(
F
(
x
)
|
w
i
,
z
∗
)
c
(
w
i
)
⋅
g
(
F
(
x
)
|
w
i
,
z
∗
)
为所有
c
(
w
j
)
⋅
g
(
F
(
x
)
|
w
j
,
z
∗
)
,
j
=
1
,
.
.
.
,
N
c
(
w
j
)
⋅
g
(
F
(
x
)
|
w
j
,
z
∗
)
,
j
=
1
,
.
.
.
,
N
中的最小的。其他定义子问题偏好区域的方法可参见【25,26】。
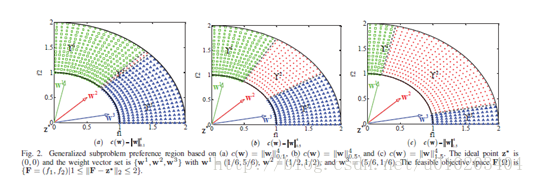
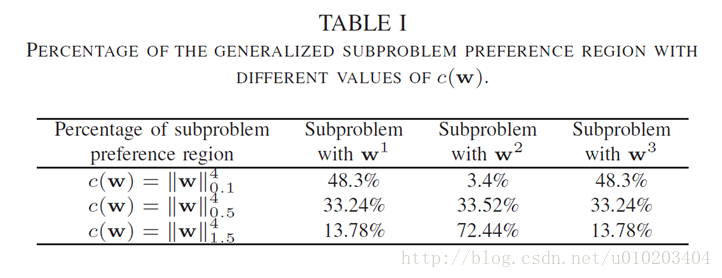
基于(14),
c
(
w
)
c
(
w
)
对于用改进Tchebycheff分解划分可行目标空间的影响如图2和表I所示。
在图2,使用了
c
(
w
)
=
∥
w
∥
4
p
c
(
w
)
=
‖
w
‖
p
4
且
p
p
在三张子图中分别被设为
,
0.5
0.5
,和
1.5
1.5
。图表表明,提高
p
p
值会缩小边界问题的偏好区域,即,与
和
w
3
w
3
关联的子问题,会增加居间问题的偏好区域,即,与
w
2
w
2
关联的第二个子问题。表I总结了泛化子问题偏好区域占可行目标空间的比率。
调节
c
(
w
)
c
(
w
)
能调整子问题偏好区域,因此,更多的更新机会会被分配到更感兴趣的子问题从而加速其收敛。例如,MOEA/D用三个子问题在双目标ZDT4【27】和DTLZ4【28】问题的测试如图2所示。广泛使用的模拟二进制交叉(simulated binary crossover,SBX)和多项式变异(polynomial mutation)【29】应用于生成子代。使用
c
(
w
)
c
(
w
)
的不同设定,关联于
w
1
w
1
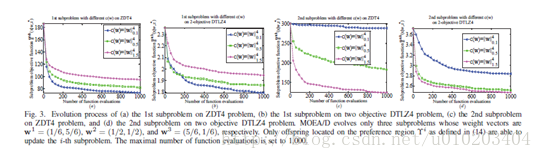
的第一个子问题拥有最大的偏好区域,示于图2(a),且收敛最快,示于图3(a)和(b),这对应于
c
(
w
)
=
∥
w
∥
4
0.1
c
(
w
)
=
‖
w
‖
0.1
4
。同样地,当
c
(
w
)
=
∥
w
∥
4
1.5
c
(
w
)
=
‖
w
‖
1.5
4
时,第二个子问题具有三者中最大的偏好区域,如图2所示,并取得了最快的收敛率,如图3(c)和(d)所示。观察可以得出,具有更大偏好区域的子问题更有可能被频繁更新,不断被改善,这将导致更快的收敛率。
提升划分全部子问题改善空间的均匀度:
为阐明这一问题,基于最大适应度提升标准,我们首次如下给出子问题改善区域的定义:
Υ
i
=
{
F
(
y
)
|
y
∈
Ω
,
g
(
F
(
y
)
|
w
i
,
z
∗
)
<
g
(
F
(
x
i
)
|
w
i
,
z
∗
)
,
Υ
i
=
{
F
(
y
)
|
y
∈
Ω
,
g
(
F
(
y
)
|
w
i
,
z
∗
)
<
g
(
F
(
x
i
)
|
w
i
,
z
∗
)
,
i
=
arg
max
1
≤
j
≤
N
{
c
(
w
)
⋅
[
g
(
F
(
x
i
)
|
w
j
,
z
∗
)
−
g
(
F
(
y
)
|
w
j
,
z
∗
)
]
}
}
i
=
arg
max
1
≤
j
≤
N
{
c
(
w
)
⋅
[
g
(
F
(
x
i
)
|
w
j
,
z
∗
)
−
g
(
F
(
y
)
|
w
j
,
z
∗
)
]
}
}
其中,
x
i
x
i
为第
i
i
个子问题的当前解。不等式
表明子代
y
y
对于第
个子问题比当前解
x
x
具有更好的适应值。(15)中最后的约束确认取得最大适应值提升的子问题。
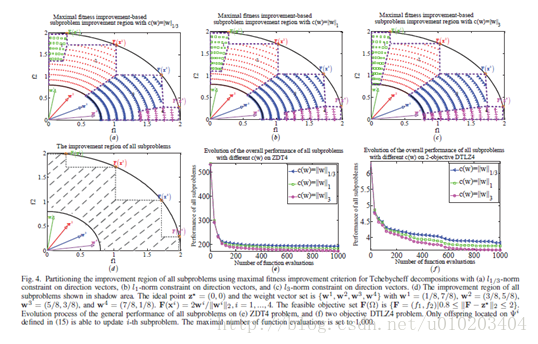
一个所有子问题提升区域的示例如图4(d)所示。通过使用(15)和改进Tchebycheff分解,
对所有子问题提升区域的划分的影响示于图4(a)-(c)。使用了
c
(
w
)
=
∥
w
∥
p
c
(
w
)
=
‖
w
‖
p
,且在图4(a)-(c)中2,
p
p
分别被设为
,
1
1
,和
。结果表明,提升
p
p
值能提升划分所有子问题提升区域的均匀度。此现象对于可行目标空间的边界区域更为明显,即,图4(a)-(c)中的
和
Υ
4
Υ
4
。
通过
c
(
w
)
c
(
w
)
,算法能够调节提升区域的均匀度以提高算法的性能。一个简单的示例如图4(a)-(c)所示,其中,MOEA/D融合了使用不同
c
(
w
)
c
(
w
)
设定的四个均匀的子问题。双目标ZDT4和DTLZ4问题被选作测试问题。多项式变异和SBX应用于生成子代。第
i
i
个子问题的当前解将被子代
更新,若其对应的目标向量位于
Υ
i
Υ
i
。提升区域的均匀划分将使所有的子问题得到更好的一般结果,如图4(e)-(f)所示。
IV. 基于最大适应值改善的种群更新策略
种群更新机制是MOEAs的关键组成,近年来已被充分研究。例如,基于差分进化(differential evolution,DE)【17】的MOEA/D,其限制了一个子代解能更新的父代解的数目。自适应全局替换MOEA/D(MOEA/D with an adaptive global replacement,MOEA/D-AVR)【19】基于最小函数值用一个新生成解替换父代解。基于稳定匹配模型的MOEA/D【30】在更新种群时,使用了一个稳定匹配模型来使每个子问题与一个单一解匹配,因此不同子问题有不同解。为提升种群的多样性,Li等人【31】进一步提出了基于交互关系的选择来选取精英解使其在进化过程中存活。基于一种泛化资源调度策略的MOEA/D【32】使用一种全局替换策略更新子问题解。这些种群更新策略已成功地提升了MOEA/D的性能,然而,它们大多是设计用于只是优化了一部分子问题的表现【17】【19】【32】。

为提升算法性能,本文提出了一种基于最大适应值提升的全局种群更新策略,示于算法1。尤其,对于目标子问题给定一般解
y
y
,在算法1的前两步,
y
y
能够取得最大适应值提升的子问题
l
l
可以识别如下
(16)
之后,在第3步,相应的解
x
l
x
l
被
y
y
替换,若
y
y
在子问题
l
l
的表现优于
。最后,为提升所提出的算法的鲁棒性,少量的父代解(不超过一个预定义的数目
n
r
−
1
n
r
−
1
)同样被随机选择并被
y
y
替换,如第4步所示。使用不同
p
p
-Tchs的影响在实验研究中被考察,其基于如下公式:
算法1给出的种群更新策略基于
p
p
-Tch,但是,在实验研究中使用的是2-Tch。选择
的原因是,首先
p
p
应该大于1,以提升子问题更新区域的均匀度,并且,
优于
p
>
2
p
>
2
,因为,相比于其他更大的
p
p
值,在2-Tch中,对于欧氏距离来说,子问题目标函数具有一个更加清晰的几何属性。2-Tch的一个子问题定义如下:
(17)
其中,
λ
=
(
λ
1
,
…
,
λ
m
)
λ
=
(
λ
1
,
…
,
λ
m
)
且
∥
λ
∥
2
=
1
‖
λ
‖
2
=
1
及
λ
1
,
…
,
λ
m
≥
0
λ
1
,
…
,
λ
m
≥
0
。
在算法1中,适应值的提升使用
g
p
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
p
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
g
p
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
p
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
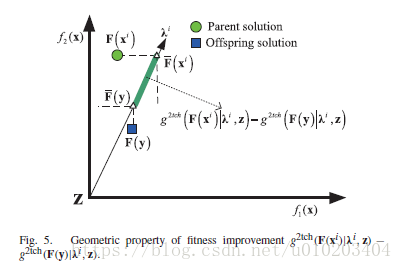
进行计算。此适应值提升在2-Tch的相应的几何属性示于图5。按照命题6,适应值提升计算如下:
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
=
∥
F
¯
¯
¯
¯
(
x
i
)
−
z
∥
2
−
∥
F
¯
¯
¯
¯
(
y
)
−
z
∥
2
=
∥
F
¯
¯
¯
¯
(
x
i
)
−
F
¯
¯
¯
¯
(
y
)
∥
2
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
=
‖
F
¯
(
x
i
)
−
z
‖
2
−
‖
F
¯
(
y
)
−
z
‖
2
=
‖
F
¯
(
x
i
)
−
F
¯
(
y
)
‖
2
其中
F
¯
¯
¯
¯
(
x
i
)
=
z
+
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
⋅
λ
i
F
¯
(
x
i
)
=
z
+
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
⋅
λ
i
F
¯
¯
¯
¯
(
y
)
=
z
+
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
⋅
λ
i
F
¯
(
y
)
=
z
+
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
⋅
λ
i
其实,这是
F
¯
¯
¯
¯
(
y
)
F
¯
(
y
)
到
F
¯
¯
¯
¯
(
x
i
)
F
¯
(
x
i
)
的距离,如图5所示。
与其他两种具有代表性策略,即MOEA/D-AGR使用的基于最小适应值的策略与MOEA/D使用的随机提升策略,所提出的基于最大适应值提升的策略具有如下优点:
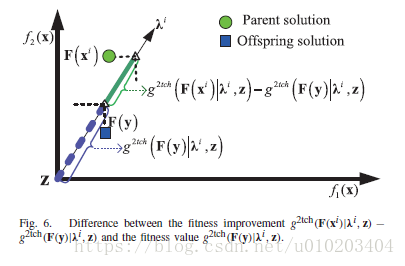
-
好的子代个体在提出的策略中能够存活更长时间。为解释这一点,适应值提升与适应值的区别首先可以使用一个双目标优化问题在图6进行说明。比如,在用一个子代
y
y
更新了一个特定子问题
i
i
之后,相应的适应值提升
和新的适应值
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
g2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
分别使用实线和虚线部分表示。按照图6的注释,一个两步的例子进一步示于图7,以区分三种种群更新策略的工作过程。尤其,两个有潜力的解
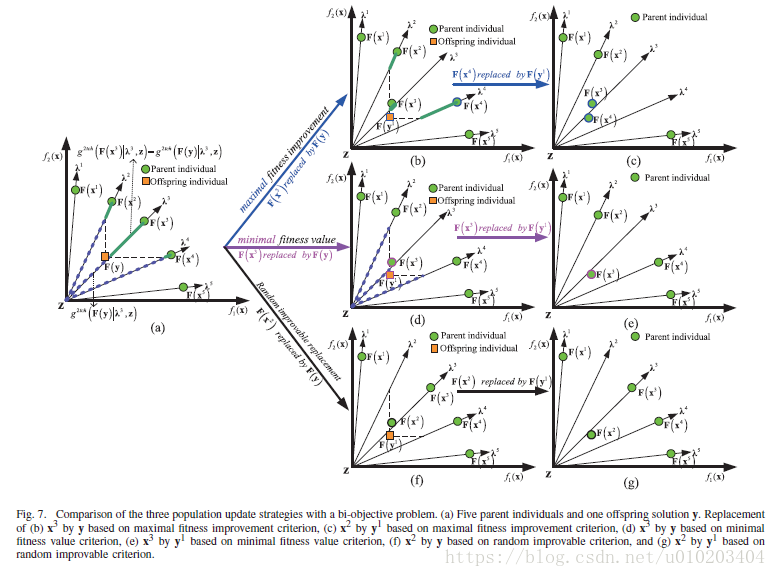
y
y
和
y
1
y1
被生成,并用于依次更新种群。在图7(a)的例子中,第一个有潜力的子代解
y
y
占优三个父代解
x
2
x2
,
x
3
x3
和
x
4
x4
。解
y
y
在第三个子问题同时取得最大适应值提升与最小适应值由于:
arg
max
1
≤
i
≤
5
[
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
]
=
3
arg
max
1
≤
i
≤
5
[
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
]
=
3
arg
min
1
≤
i
≤
5
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
=
3
arg
min
1
≤
i
≤
5
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
=
3
因此,在第一步中,基于最大适应值提升与最小适应值的种群更新策略使用子代
y
y
更新
x
3
x3
,分别示于图7(b)和(d)。MOEA/D所用的策略随机替换一个可提升的父代个体,比如图7(f)的
x
2
x2
。为清晰起见,一个新生成的子代解
y
y
用于替换最多一个父代个体,即,
n
r
=
1
nr
=
1
,示于图7。在第二步,如图7(b),(d)和(f)所示,给定第二个潜力解
y
1
y1
,三种策略分别用
y
1
y1
替换了
x
4
x4
,
x
3
x3
与
x
2
x2
,如图7(c),(e)和(g)所示。其原因如下:
arg
max
1
≤
i
≤
5
[
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
]
=
4
arg
max
1
≤
i
≤
5
[
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
]
=
4
arg
min
1
≤
i
≤
5
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
=
3
arg
min
1
≤
i
≤
5
g
2
t
c
h
(
F
(
y
)
|
λ
i
,
z
)
=
3
在图7(f)中,MOEA/D所用的更新策略能够随机用
y
1
y1
替换
x
2
x2
或
x
3
x3
。图7(g)假定
x
2
x2
被
y
1
y1
替换。可以观察到,所提出的基于最大适应值提升策略成功地保留了第一个潜力个体
y
y
,即,图7(c)中的
x
3
x3
,然而,另两个策略舍弃了
y
y
,如图7(e)和(g)所示。换句话说,在提出的更新策略中,好的解更可能幸存。
-
提出的策略提升了在所有子问题上的泛化性能,即,
∑
N
i
=
1
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
∗
)
∑i
=
1
N
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
∗
)
,而不是部分子问题。使用
∑
N
i
=
1
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
∗
)
∑i
=
1
N
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
∗
)
来评估整个种群性能的合理性亦将在节VI的
R
2
t
c
h
2
R2
2
t
c
h
指标(20)的定义中解释。给定一个种群
A
=
{
x
1
,
…
,
x
N
}
A=
{
x
1
,
…
,
x
N
}
,如下假定是合理的:
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
∗
)
=
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
g2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
∗
)
=
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
其中,
x
i
xi
为MOEA/D中子问题
i
i
的当前最优解。理想目标向量
一般是事先未知的,故【3】中提出的用参考点
z
z
估计
z
∗
z∗
的方法在本文采用了。所有子问题的一般性能能够通过将
A
A
中所有个体的适应值相加而进行估计,其为
g
2
t
c
h
(
F
(
A
)
|
D
,
z
)
=
∑
i
=
1
N
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
g2
t
c
h
(
F
(
A
)
|
D
,
z
)
=
∑
i
=
1
N
g
2
t
c
h
(
F
(
x
i
)
|
λ
i
,
z
)
其中,
D
=
{
λ
1
,
…
,
λ
N
}
D=
{
λ
1
,
…
,
λ
N
}
且较小的
g
2
t
c
h
(
F
(
A
)
|
D
,
z
)
g2
t
c
h
(
F
(
A
)
|
D
,
z
)
意味着整个种群或所有子问题的较好的一般性能。
令所有三个比较的策略由同一初始种群
A
A
开始,一个新生成的子代解
y
y
用于只替换一个父代解。不失一般性,提出的基于最大适应值提升的策略应该更新子问题
l
l
,而其他两种策略更新子问题
。根据(16)中最大适应值提升的定义,很明显:
g
2
t
c
h
(
F
(
x
l
)
|
λ
l
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
l
,
z
)
≥
g
2
t
c
h
(
F
(
x
j
)
|
λ
j
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
j
,
z
)
g
2
t
c
h
(
F
(
x
l
)
|
λ
l
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
l
,
z
)
≥
g
2
t
c
h
(
F
(
x
j
)
|
λ
j
,
z
)
−
g
2
t
c
h
(
F
(
y
)
|
λ
j
,
z
)
相应地,更新子问题
l
l
得到的新种群的适应值和小于或等于更新子问题
的,即:
g
2
t
c
h
(
F
(
A
)
|
D
,
z
)
−
g
2
t
c
h
(
F
(
x
l
)
|
λ
l
,
z
)
+
g
2
t
c
h
(
F
(
y
)
|
λ
l
,
z
)
≤
g
2
t
c
h
(
F
(
A
)
|
D
,
z
)
−
g
2
t
c
h
(
F
(
x
j
)
|
λ
j
,
z
)
+
g
2
t
c
h
(
F
(
y
)
|
λ
j
,
z
)
g
2
t
c
h
(
F
(
A
)
|
D
,
z
)
−
g
2
t
c
h
(
F
(
x
l
)
|
λ
l
,
z
)
+
g
2
t
c
h
(
F
(
y
)
|
λ
l
,
z
)
≤
g
2
t
c
h
(
F
(
A
)
|
D
,
z
)
−
g
2
t
c
h
(
F
(
x
j
)
|
λ
j
,
z
)
+
g
2
t
c
h
(
F
(
y
)
|
λ
j
,
z
)
换句话说,提出的策略能够在所有子问题上得到更好的一般性能,相比于另外两种在MOEA/D和MOEA/D-AGR使用的更新策略。
V. 提出的MOEA/D-2TCHMFI的细节

2-Tch与提出的基于最大适应值改进的种群更新策略被组合到MOEA/D框架中,以组成新算法,称为MOEA/D-2TCHMFI。MOEA/D-2TCHMFI致力于就解的收敛性而言,提升MOEA/D,在算法2进行了概述。权重向量/方向向量的选择对于寻找在PF均匀分布的解是关键的。对于一个分解方法,权重的一种最优分布能够根据【5】-【7】得到,若一个MOP的PF的几何形状是事先知道的,且提供了分布良好的Pareto最优解集的清晰定义的话。
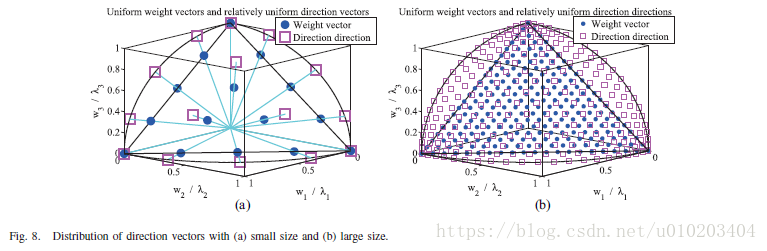
在算法2中,步骤1设置方向向量
{
λ
1
,
…
,
λ
N
}
{
λ
1
,
…
,
λ
N
}
如下:
λ
i
=
w
i
∥
w
i
∥
2
,
i
=
1
,
…
,
N
λ
i
=
w
i
‖
w
i
‖
2
,
i
=
1
,
…
,
N
其中,
{
w
1
,
…
,
w
N
}
{
w
1
,
…
,
w
N
}
为由【3】中建议的方法随机生成的权重向量。均匀权重向量
{
w
1
,
…
,
w
N
}
{
w
1
,
…
,
w
N
}
及相应的方向向量
{
λ
1
,
…
,
λ
N
}
{
λ
1
,
…
,
λ
N
}
的可视化在图8中。步骤2仅选择了
⌊
N
/
5
⌋
⌊
N
/
5
⌋
子问题,这基于它们在每一代生成子代的最近的表现。步骤3使用2-Tch与基于最大适应值提升标准的种群更新策略来迭代地进化选择的子问题。尤其地,在步骤3.1中,每个子问题通过主要来自其邻域的子问题的信息进行优化。参考点
z
z
在步骤3.2更新,父代解在步骤3.3根据算法1进行更新。在步骤3.4中,若代数
g
e
n
g
e
n
可以被
30
30
整除,子问题
i
i
的适应值在近30代的相应的减少计算如下:
其中,
x
i
,
g
e
n
x
i
,
g
e
n
与
x
i
,
g
e
n
−
30
x
i
,
g
e
n
−
30
分别为在当前代与代数
g
e
n
−
30
g
e
n
−
30
时子问题
i
i
的解。根据【16】,MOEA/D-2TCHMFI基于
更新每个子问题
π
i
,
i
=
1
,
…
,
N
π
i
,
i
=
1
,
…
,
N
,如下:
π
i
=
1
,
i
f
Δ
i
>
0.001
π
i
=
1
,
i
f
Δ
i
>
0.001
π
i
=
(
0.95
+
0.05
×
Δ
i
0.001
)
×
π
i
,
o
t
h
e
r
w
i
s
e
π
i
=
(
0.95
+
0.05
×
Δ
i
0.001
)
×
π
i
,
o
t
h
e
r
w
i
s
e
最后,在步骤4,若达到预定义的最大适应值评估次数,算法终止。
VI. 基于2-Tch的一元
R
2
R
2
指标
为证实所提算法的有效性,本节介绍了一种基于2-Tch的
R
2
R
2
指标。
R
2
R
2
首先由Hanson与Jaszkiewicz【15】在1998年提出。最近,
R
2
R
2
指标日益吸引到了研究兴趣【33】-【38】。
R
2
R
2
指标的大多数研究【15】,【34】-【38】是基于传统的Tchebycheff分解的,少数【33】基于改进的Tchebycheff分解。然而,基于这两种Tchebycheff分解方法的
R
2
R
2
指标的几何属性并不易懂。在这里,具有更清晰的几何属性的新的
R
2
R
2
指标被提出以估计超体积度量,如下:
R
2
t
c
h
2
(
A
|
z
∗
)
=
∫
λ
∈
Λ
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
}
d
u
∫
Λ
d
u
R
2
2
t
c
h
(
A
|
z
∗
)
=
∫
λ
∈
Λ
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
}
d
u
∫
Λ
d
u
(18)
其中
Λ
=
{
λ
=
(
λ
1
,
…
,
λ
m
)
|
λ
i
≥
0
,
i
=
1
,
…
,
m
,
∥
λ
∥
2
=
1
}
Λ
=
{
λ
=
(
λ
1
,
…
,
λ
m
)
|
λ
i
≥
0
,
i
=
1
,
…
,
m
,
‖
λ
‖
2
=
1
}
且
d
u
d
u
为在
Λ
Λ
上的Lebesgue度量【39】。若没有决策者(DM)的参考信息,可以合理地假定方向向量
λ
λ
服从
Λ
Λ
上的一个均匀分布。
∫
Λ
d
u
∫
Λ
d
u
等于
2
−
m
2
−
m
倍的
m
m
维单位超球的表面积,因为
为单位超球表面在第一象限的部分,其中,
m
m
为目标函数的数目。子问题目标函数
可看作为DM的一个效用函数/参照【20】。给定种群
A
A
的所有个体中的选择权,DM倾向于选择具有
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
}
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
}
的那一个,示于图9(a)。
R
2
t
c
h
2
(
A
|
z
∗
)
R
2
2
t
c
h
(
A
|
z
∗
)
越小,DM所期望的效用/参照就越好。
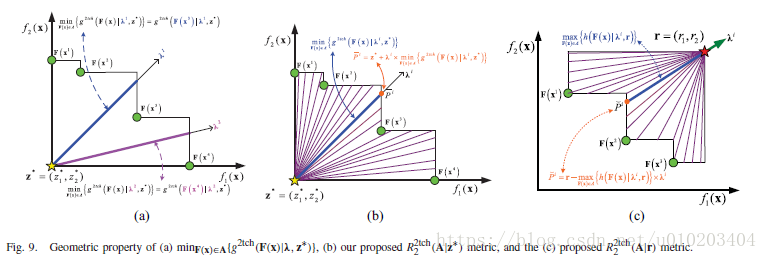
所提出的
R
2
t
c
h
2
R
2
2
t
c
h
度量的几何属性示于图9(b)。尤其,一个点
P
¯
¯
¯
¯
i
P
¯
i
被引入以便于
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
的计算,即:
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
=
∥
P
¯
¯
¯
¯
i
−
z
∗
∥
2
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
=
‖
P
¯
i
−
z
∗
‖
2
很容易证明:
R
2
t
c
h
2
(
A
|
z
∗
)
≈
∑
M
i
=
1
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
M
R
2
2
t
c
h
(
A
|
z
∗
)
≈
∑
i
=
1
M
min
F
(
x
)
∈
A
{
g
2
t
c
h
(
F
(
x
)
|
λ
i
,
z
∗
)
}
M
=
∑
M
i
=
1
∥
P
¯
¯
¯
¯
i
−
z
∗
∥
2
M
=
∑
i
=
1
M
‖
P
¯
i
−
z
∗
‖
2
M
其中,
M
M
为方向向量集的大小。因此,所提出的
指标的几何属性实际上为连接
z
∗
z
∗
与
P
¯
¯
¯
¯
i
P
¯
i
的线段的平均长度。
P
¯
¯
¯
¯
i
P
¯
i
的分布很适合估计集
A
=
{
x
1
,
x
2
,
x
3
,
x
4
}
A
=
{
x
1
,
x
2
,
x
3
,
x
4
}
的超体的表面。按【35】的建议,
R
2
t
c
h
2
(
A
|
z
∗
)
R
2
2
t
c
h
(
A
|
z
∗
)
能够用于估计集
A
A
的超体积。(20)中的一个简化的形式的解释提供于补充材料的附录A中。如补充材料的附录B所证明,所提出的一元指标
R
2
t
c
h
2
R
2
2
t
c
h
(DM所期望的效用/参考)是对于Pareto占优严格单调的,这对于一种评估指标【40】是必要的。
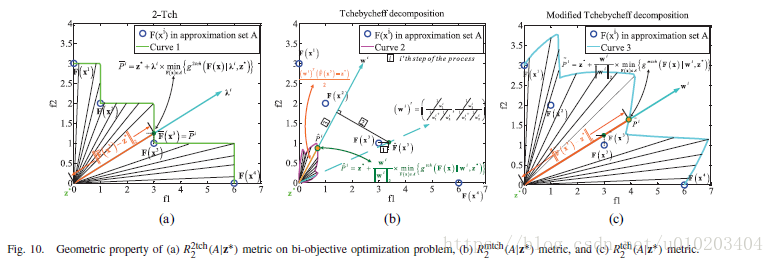
基于2-Tch的
R
2
R
2
指标对于另外两种基于传统Tchebycheff分解和改进的Tchebycheff分解的指标的优势示于图10。通过分别用
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
与
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
g
m
t
c
h
(
F
(
x
)
|
w
,
z
∗
)
替换(18)中的
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
g
2
t
c
h
(
F
(
x
)
|
λ
,
z
∗
)
,可以令
R
t
c
h
2
(
A
|
z
∗
)
R
2
t
c
h
(
A
|
z
∗
)
与
R
m
t
c
h
2
(
A
|
z
∗
)
R
2
m
t
c
h
(
A
|
z
∗
)
分别表示这两种指标。图10展示了
R
2
t
c
h
2
(
A
|
z
∗
)
R
2
2
t
c
h
(
A
|
z
∗
)
,
R
t
c
h
2
(
A
|
z
∗
)
R
2
t
c
h
(
A
|
z
∗
)
与
R
m
t
c
h
2
(
A
|
z
∗
)
R
2
m
t
c
h
(
A
|
z
∗
)
在一个双目标优化问题中的几何含义。
R
2
t
c
h
2
(
A
|
z
∗
)
R
2
2
t
c
h
(
A
|
z
∗
)
,
R
t
c
h
2
(
A
|
z
∗
)
R
2
t
c
h
(
A
|
z
∗
)
与
R
m
t
c
h
2
(
A
|
z
∗
)
R
2
m
t
c
h
(
A
|
z
∗
)
分别为从理想点
z
∗
z
∗
到曲线1-3的平均距离。可以从图10(a)看出,
R
2
t
c
h
2
(
A
|
z
∗
)
R
2
2
t
c
h
(
A
|
z
∗
)
表示从理想点
z
∗
z
∗
到非占优解集的超体表面的的平均距离。相比而言,
R
t
c
h
2
(
A
|
z
∗
)
R
2
t
c
h
(
A
|
z
∗
)
与
R
m
t
c
h
2
(
A
|
z
∗
)
R
2
m
t
c
h
(
A
|
z
∗
)
均不能表明与非占优解集的分布的直观关系,示于图10(b)和(c)中。
VII. 实验研究
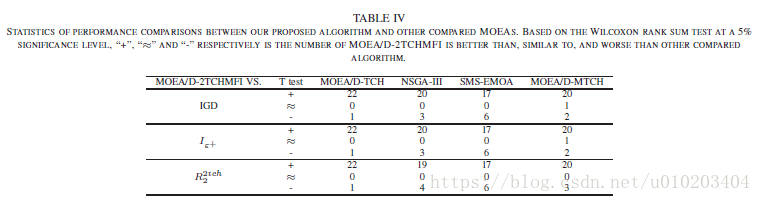
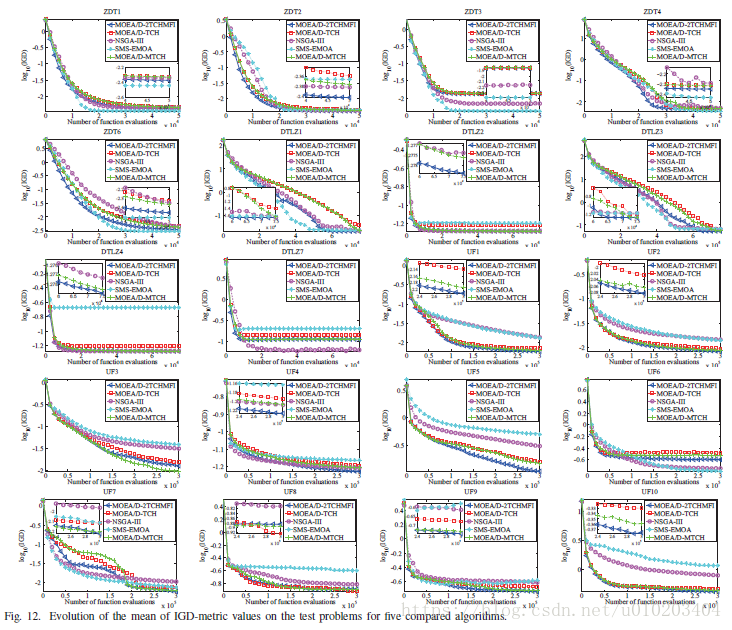
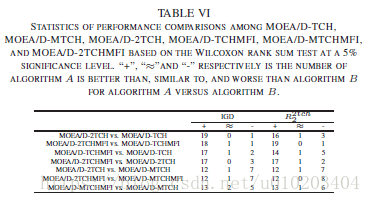
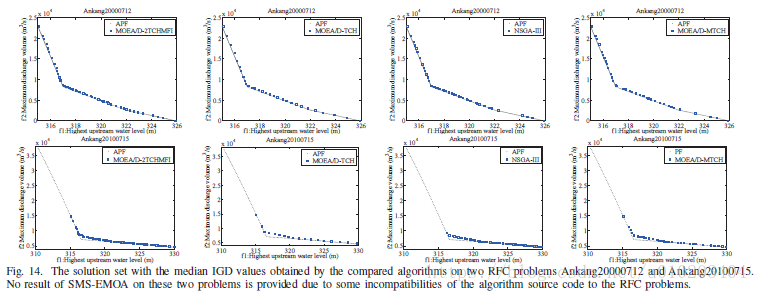

参考文献