深度广度优先遍历最小生成树

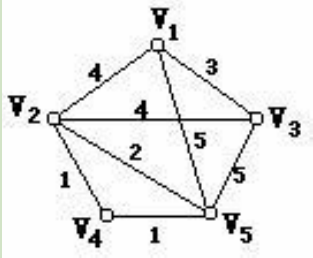
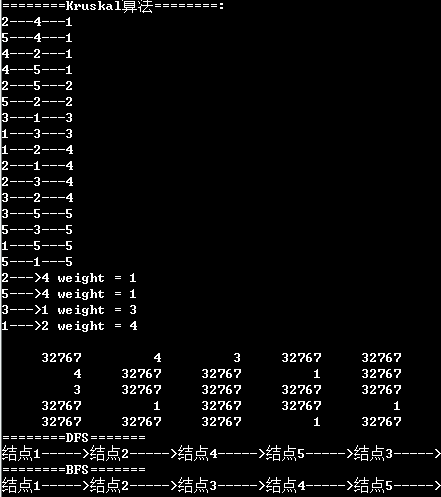
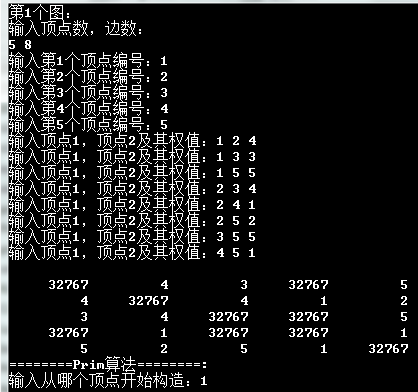
怎么用图的深度和广度优先遍历来遍历树呢？我是这样想的，把树构造成图就行了。

// 图的遍历.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include "LinkQueue.h"
#include <stdio.h>
#include <stdlib.h>
#define VRType int//在这里是权值类型
#define MAX_VERTEX_NUM 10//最大顶点个数
#define VertexType char //顶点类型
#define INFINITY 32767 //无穷大，不连通
//边的结构
typedef struct ArcCell{
	VRType adj;//权值
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
//图的结构
typedef struct {
	VertexType vexs[MAX_VERTEX_NUM];//顶点向量
	AdjMatrix arcs;//邻接矩阵
	int vexnum,arcnum;//顶点数，边数
}MGraph;
//辅助数组，记录从U到V-U的最小代价的边
typedef struct {
	VertexType adjvex;
	VRType lowcost;
}Closedge;
//
typedef struct edge{
	int begin;//起始顶点位置
	int end;//终点位置
	VRType weight;//权重
}Edge[100];

//函数声明
void CreateMGraph(MGraph &G);//创建图
void PrintGraph(MGraph G);//打印图
void Prim(MGraph G,VertexType v,MGraph &TG);//
void Kruskal(MGraph G,MGraph &TG);
//找到结点v在图G中的序号，返回，没找到返回-1
int LocateVex(MGraph G,VertexType v);
void InitGraph(MGraph &G,int arcnum,int vertexnum);//初始化图
//把G图中的一条边添加到TG中去
void AddArc(MGraph &TG,MGraph G,VertexType v1,VertexType v2,VRType weight);
//返回v结点的第一个邻接顶点的序号,没找到返回-1
int FirstAdjVex(MGraph G,VertexType v);
//返回v相对于w的下一个邻接点，若w是v的最后一个邻接顶点，返回-1
int NextAdjVex(MGraph G,VertexType v,VertexType w);
//递归深度优先遍历图
int visited[MAX_VERTEX_NUM] = {0};//访问标记数组
void DFSG(MGraph G,void (*Visit)(VertexType));
void DFS(MGraph G,int i);
//非递归广度优先遍历图
void BFSG(MGraph G,void(*Visit)(VertexType));
//对结点的操作函数
void (*VisitFunc)(VertexType v);//全局变量，方便访问VisitNode
void VisitNode(VertexType v);

int main(){
	int i=1;
	MGraph G,TG;
	VertexType v;
	while(i){
		InitGraph(TG,0,1);
		printf("第%d个图：\n",i++);
		CreateMGraph(G);
		PrintGraph(G);
		//Prim算法
		printf("========Prim算法========:\n输入从哪个顶点开始构造：");
		fflush(stdin);
		scanf("%c",&v);
		Prim(G,v,TG);
		PrintGraph(TG);
		/*---------------
		for(int k=0;k<TG.vexnum;k++){
			printf("%c-%d----",TG.vexs[k],LocateVex(TG,TG.vexs[k]));
		}
		printf("\n");
		/*---------------*/
		printf("========DFS=======\n");
		DFSG(TG,VisitNode);
		printf("\n========BFS=======\n");
		BFSG(TG,VisitNode);
		//Kruskal算法
		printf("\n========Kruskal算法========:\n");
		InitGraph(TG,0,1);//重新初始化TG
		Kruskal(G,TG);
		PrintGraph(TG);
		printf("========DFS=======\n");
		DFSG(TG,VisitNode);
		printf("\n========BFS=======\n");
		BFSG(TG,VisitNode);
		system("pause");
	}
	return 0;
}
//函数实现
int minimum(Closedge *closedge,MGraph G){
	int i=0,j,k,min;
	while(!closedge[i].lowcost){//找到第一个权值不为零的
		i++;
	}
	min = closedge[i].lowcost;
	k = i;
	for(j=i+1;j<G.vexnum;j++){
		if(closedge[j].lowcost >0 && min >closedge[j].lowcost){
			min = closedge[j].lowcost;
			k = j;
		}
	}
	return k;
}
/*---------*/
void printCloseE(Closedge*close,int n){
	for(int i=0;i<n;i++){
		printf("closedge[%d].adjvex=%c || closedge[%d].lowcost=%d\n",i,close[i].adjvex,i,close[i].lowcost);
	}
}
/*---------*/
void Prim(MGraph G,VertexType v,MGraph &TG){
	int k = LocateVex(G,v),i=0,j=0;
	Closedge closedge[MAX_VERTEX_NUM];
	//辅助矩阵初始化
	for(i=0;i<G.vexnum;i++){
			closedge[i].adjvex = v;
			closedge[i].lowcost = G.arcs[k][i].adj;
	}
	closedge[k].lowcost = 0;//把结点v加入集合U中
	/*--------
	printCloseE(closedge,G.vexnum);
	/*--------*/
	for(i=1;i<G.vexnum;i++){
		k = minimum(closedge,G) ;//求出最小生成树的下一个节点，第k顶点
		printf("%c--->%c\n",closedge[k].adjvex,G.vexs[k]);

		AddArc(TG,G,closedge[k].adjvex,G.vexs[k],closedge[k].lowcost);
		closedge[k].lowcost = 0;//第k结点加入U
		//重新选择最小边
		for(j=0;j<G.vexnum;j++){
			if( G.arcs[k][j].adj < closedge[j].lowcost){
				closedge[j].adjvex = G.vexs[k];
				closedge[j].lowcost = G.arcs[k][j].adj;
			}
		}
		/*--------
		printf("===============\n");
		printCloseE(closedge,G.vexnum);
		/*--------*/
	}
}
//打印边数组
void print(Edge *E,int n,MGraph G){
	for(int i=0;i<n;i++){
		printf("%c---%c---%d\n",G.vexs[E[i]->begin],G.vexs[E[i]->end],G.arcs[E[i]->begin][E[i]->end].adj);
	}
}
//按权值从小到大排序
int cmp(const void *a,const void *b){
	return ((struct edge*)a)->weight - ((struct edge*)b)->weight;
}
void Kruskal(MGraph G,MGraph &TG){
	Edge *E = (Edge*)malloc(sizeof(Edge)*G.arcnum*2) ;
	int i=0,j=0,k=0;
	for(i=0;i<G.vexnum;i++){
		for(j=0;j<G.vexnum;j++){
			if(G.arcs[i][j].adj != INFINITY){
				E[k]->begin = i;
				E[k]->end = j;
				E[k]->weight = G.arcs[i][j].adj;
				k++;
			}
		}
	}
	qsort(E,k,sizeof(E[0]),cmp);
	print(E,k,G);
	int *vset = (int *)malloc(sizeof(int)*G.vexnum);
	for (i=0;i<G.vexnum;i++){                                  //初始化辅助数组    
        vset[i]=i;  
    }  
    k=1;                                                   //生成的边数，最后要刚好为总边数   
    j=0;                                                   //E中的下标   
    while (k<G.vexnum){   
        int set1 = vset[E[j]->begin];  
        int set2 = vset[E[j]->end];                                  //得到两顶点属于的集合   
		/*----------
		printf("set1 = %d||set2 = %d\n",set1,set2);
		/*----------*/
        if (set1!=set2){                                    //不在同一集合内的话，把边加入最小生成树   
			printf("%c--->%c weight = %d\n",G.vexs[E[j]->begin],G.vexs[E[j]->end],E[j]->weight);

			//加进边
			AddArc(TG,G,G.vexs[E[j]->begin],G.vexs[E[j]->end],E[j]->weight);
            k++;  
            for (i=0;i<G.vexnum;i++)  
            {  
                if (vset[i]==set2)  
                {  
                    vset[i]=set1; 
                }  
            }
			/*----------
			for(int c=0;c<G.vexnum;c++){
				printf("vset[%d]=%d ",c,vset[c]);
			}
			printf("\n");
			/*----------*/
        }  
        j++;  
    }  
	free(vset);
	free(E);
}
void CreateMGraph(MGraph &G){
	printf("输入顶点数，边数：");
	int vexnum=0,arcnum=0;
	scanf("%d %d",&vexnum,&arcnum);
	//初始化矩阵
	InitGraph(G,arcnum,vexnum);

	int i=0,j=0;
	for(i=0;i<G.vexnum;i++){
		printf("输入第%d个顶点编号：",i+1);
		fflush(stdin);
		scanf("%c",&G.vexs[i]);
	}
	char v1,v2;
	int w;
	for(int k=0;k<G.arcnum;k++){
		printf("输入顶点1，顶点2及其权值：");
		fflush(stdin);
		scanf("%c %c %d",&v1,&v2,&w);
		i = LocateVex(G,v1);
		j = LocateVex(G,v2);
		G.arcs[i][j].adj = w;
		G.arcs[j][i] = G.arcs[i][j];//对称边
	}
}
int LocateVex(MGraph G,VertexType v){
	for(int i=0;i<G.vexnum;i++){
		if(v == G.vexs[i]){
			return i;
		}
	}
	return -1;
}
//初始化一个图
void InitGraph(MGraph &G,int arcnum,int vertexnum){
	G.arcnum = arcnum;
	G.vexnum = vertexnum;
	for(int i=0;i<MAX_VERTEX_NUM;i++){
		for(int j=0;j<MAX_VERTEX_NUM;j++){
			G.arcs[i][j].adj = INFINITY;
		}
	}
}
//打印一个图，二维
void PrintGraph(MGraph G){
	printf("\n");
	for(int i=0;i<G.vexnum;i++){
		for(int j=0;j<G.vexnum;j++){
			printf("%10d",G.arcs[i][j].adj);
			/*-----------
			printf("%d",G.arcs[i][j].adj);
			if(G.arcs[i][j].adj!=INFINITY){
				printf("(%c-%d)",G.vexs[i],i);
			}
			printf("\t");
			/*-------------*/
		}
		printf("\n");
	}
}
//向TG图中加一条边
void AddArc(MGraph &TG,MGraph G,VertexType v1,VertexType v2,VRType weight){
	int i = LocateVex(G,v1);
	int j = LocateVex(G,v2);
	TG.vexs[i] = v1;
	TG.vexs[j] = v2;
	/*------------
	printf("%c-%d\n%c-%d",G.vexs[i],i,G.vexs[j],j);
	/*------------*/
	if(i>=0 && j>=0){
		TG.arcs[i][j].adj = weight;
		TG.arcs[j][i].adj = weight;
		TG.arcnum++;
		TG.vexnum++;
	}
}

int FirstAdjVex(MGraph G,VertexType v){
	int k = LocateVex(G,v);
	for(int i=0;i<G.vexnum;i++){
		if(G.arcs[k][i].adj != INFINITY){//第一个权值不为无穷大的点就是
			return i;
		}
	}
	return -1;
}
///
int NextAdjVex(MGraph G,VertexType v,VertexType w){
	int a = LocateVex(G,v);
	int b = LocateVex(G,w);
	for(int i=b+1;i<G.vexnum;i++){
		if(G.arcs[a][i].adj != INFINITY){
			return i;
		}
	}
	return -1;
}
/
void DFSG(MGraph G,void (*Visit)(VertexType)){
	int i=0;
	VisitFunc = Visit;
	for(i=0;i<G.vexnum;i++){
		visited[i] = 0;//初始化，0代表没访问
	}
	for(i=0;i<G.vexnum;i++){
		if(!visited[i]){//第i个结点没被访问，就递归搜索
			DFS(G,i);
		}
	}
}
void DFS(MGraph G,int i){
	//从第i个结点出发深度优先遍历图
	visited[i] = 1;
	VisitFunc(G.vexs[i]);
	for(int j = FirstAdjVex(G,G.vexs[i]);j>=0;j = NextAdjVex(G,G.vexs[i],G.vexs[j])){
		if(!visited[j]){
			DFS(G,j);
		}
	}
}
/
void BFSG(MGraph G,void(*Visit)(VertexType)){
	int i=0,k=0;
	for(i=0;i<G.vexnum;i++){
		visited[i] = 0;
	}
	VertexType u;
	LinkQueue Q;
	InitQueue(Q);
	for(i=0;i<G.vexnum;i++){
		if(!visited[i]){
			visited[i] = 1;
			Visit(G.vexs[i]);
			EnQueue(Q,G.vexs[i]);
			while(!QueueEmpty(Q)){
				DeQueue(Q,u);
				for(k=FirstAdjVex(G,u);k>=0;k=NextAdjVex(G,u,G.vexs[k])){
					if(!visited[k]){
						visited[k] = 1;
						Visit(G.vexs[k]);
						EnQueue(Q,G.vexs[k]);
					}
				}
			}
		}
	}
}
//
void VisitNode(VertexType v){
	printf("结点%c----->",v);
}

广度优先用到的队列：

#include <stdio.h>
#include <stdlib.h>
#define QElemType char

typedef struct QNode{
	QElemType data;
	QNode *next;
}*QueuePtr;
struct LinkQueue{
	QueuePtr front,rear;
};

void InitQueue(LinkQueue &Q){
	if(!(Q.front=Q.rear = (QueuePtr)malloc(sizeof(QNode)))){
		exit(-1);//溢出
	}
	Q.front->next = NULL;
}
void EnQueue(LinkQueue &Q,QElemType e){
	QueuePtr p;
	if(!(p = (QueuePtr)malloc(sizeof(QNode)))){
		exit(-1);
	}
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
}
int DeQueue(LinkQueue &Q,QElemType &e){
	QueuePtr p;
	if(Q.front==Q.rear){
		return -1;
	}
	p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if(Q.rear==p){
		Q.rear = Q.front;
	}
	free(p);
	return 1;
}
int QueueEmpty(LinkQueue Q){
	if(Q.front==Q.rear){
		return 1;
	}else{
		return 0;
	}
}

运行结果：

输出的排版变了一下，别忘了。。。

原文链接：https://blog.csdn.net/jimo_lonely/article/details/50170137

你可能也喜欢