前言
本文为我自己的学习笔记,是Cadence Virtuoso系列的第四篇文章,也是入门系列的文章,采用的软件版本是Cadence Virtuoso IC617。其他文章请点击上方,看我制作的Cadence Virtuoso专栏内容。
本文主要记录了如何用Cadence Virtuoso IC617仿真CMOS反相器,这将帮助学习者更加深入理解Cadence仿真,本文涉及时域仿真和多曲线仿真。
固定W与L时的输入输出特性
原理图
使用第一篇文章中提到的SMIC 0.18um工艺作为原理图使用的工艺,建立如下原理图,用于测量输出电压随输入电压的变化而变化的曲线。VDD由V2控制,设置固定值为3V,输入由V1控制,设置为变量vin。此处设置MOS的W和L为固定值,分别为220nm和180nm。
易错一:此原理图为CMOS反相器,由一个N-MOS和一个P-MOS组成。
易错二:N-MOS的B极连接到GND,P-MOS的B极连接到VDD。

为了避免篇幅太长,同时大部分仿真设置前面的文章都讲过,所以这里就一笔带过仿真的有关设置。默认现在在看这篇文章的人,已经阅读过前面的仿真V-I特性曲线的文章。
没有看过的请点击下方链接,跳转到目录中的**“设置单一变量仿真”**,里面以下提到的所有选项的详细解释。
用Cadence Virtuoso IC617仿真V-I特性曲线
设置仿真变量
选择菜单中的Launch,选择第一项ADE L。
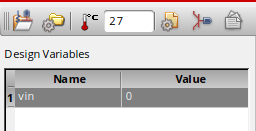
在弹出的窗口中选择Copy From Cellview,就能把原理图中的变量vin导入进来。

同时,设置变量的初始值,这里设置初始值为0。
设置仿真分析
对扫描类型进行设置。选择AED L窗口中,右边的图标。

这里设置直流DC仿真,仿真的变量是vin,范围是0-3V,点击OK确认。

最终,会在窗口中显示设置后的提示。

设置仿真输出
点击右边的图标,设置仿真输出。

在弹出的窗口中,不推荐直接输入节点名字,更推荐直接点击From Design。

我们需要仿真的是电压,而不是前面仿真V-I特性曲线中的电流,所以我们选择的是连线,而不是器件的节点。被选中的连线被标记上了颜色,其中,输入被标记成了绿色,输出标记成了红色。

回到原来窗口,可以看出,输出为电压型,命名为“net XXX”,前文提到的电流型为“NM0 / X”。点击OK确认修改。

最终,会在窗口中显示设置后的提示。

最终仿真结果
经过上面三步,可以得出仿真器中的三个子窗口里都有数据了。点击右边的开始图标,可以得到仿真结果。

得出了仿真曲线。其中红色的是输入电压曲线,绿色的是输出电压曲线。在此W和L下,vin=vout的点位于约1.16V处,即38.7% VDD处。

扫描W对输入输出特性的影响
在上一节中,介绍了固定MOS的W与L时,输入与输出的特性。为了直观地观察在不同晶体管尺寸下的电路特性,我们需要用扫描变量的方式来对电路进行仿真。
原理图
将原理图改成如下图。即,把MOS的W改成变量。这里只记录扫描W的过程,扫描L的过程同理,不再赘述。

具体的设置如下,改动的是Total Width。

仿真设置
在左边窗口中,添加所有变量并设置初值之后,选择Tools中的Parametric Analysis。

添加两个变量,都是从220nm开始扫描,扫描步进为110nm。可以通过Sweep选项框中的勾,来切换扫描的变量。点击绿色按钮开始仿真。

仿真结果
设置扫描N-MOS的W,结果如下。可以看出随着W的变大,输出曲线左移,也就是vin=vout的点左移。

设置扫描P-MOS的W,结果如下。可以看出随着W的变大,输出曲线右移,也就是vin=vout的点右移。

输入为方波时的输入输出特性
前面记录的都是输入电压作为变量,进行直流DC分析。现在将输入换成方波,进行时域分析。
原理图
在前面原理图的基础上,将输入电压源V1改成方波输入。具体如下,选取器件库中的vpulse加入原理图中。

方波信号的参数设置如下。这里主要设置其峰值范围为0-3V,周期为2ns,脉冲宽度为1ns,最终得到一个50%占空比的方波。

设置好的原理图如下。注意把MOS的W改回常数。

仿真设置
选择菜单中的Launch,选择第一项ADE L。
由于是时域分析,就不需要设置变量了,直接设置扫描类型。

设置为第一项,时域分析,设置扫描时间为10ns,即5个周期。

设置输出。

在弹出的窗口中,不推荐直接输入节点名字,更推荐直接点击From Design。

我们需要仿真的是电压,而不是前面仿真V-I特性曲线中的电流,所以我们选择的是连线,而不是器件的节点。被选中的连线被标记上了颜色,其中,输入被标记成了绿色,输出标记成了红色。

回到原来窗口,可以看出,输出为电压型,命名为“net XXX”,前文提到的电流型为“NM0 / X”。点击OK确认修改。

最终,会在窗口中显示设置后的提示。

仿真结果
经过上面三步,可以得出仿真器中的三个子窗口里都有数据了。点击右边的开始图标,可以得到仿真结果。

结果曲线图。可以看出,已经达到了反相的效果。

拖动时间轴手柄,可以拉开曲线以及选择时间,观察上升和下降沿。

经验小结
在设计中,我们一般会使 vin=vout 这个平衡点位于 0.5*VDD 处,此时两只晶体管的 Ids 相等,但由于 P-MOS 和 N-MOS 的工艺参数并不相等,这就需要我们对两只晶体管的 W / L 进行设计。
一般情况
一般情况下,可以得出以下关系。其中,K最好比2稍微大一点点,这样效果更佳。
(
W
L
)
p
=
K
(
W
L
)
n
K
≈
2
,
(
W
L
)
n
⩾
3
\Big( {W \over L} \Big)_p = K \Big( {W \over L} \Big)_n \newline \enspace \newline K \approx 2,\enspace \Big( {W \over L} \Big)_n \geqslant 3
(
L
W
)
p
=
K
(
L
W
)
n
K
≈
2
,
(
L
W
)
n
⩾
3
例如设计以下尺寸,能满足上面提到的关系。
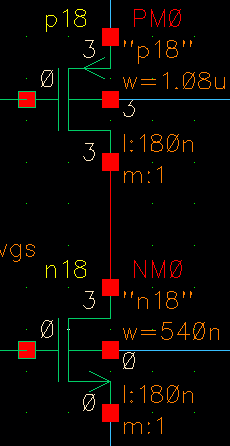
此时,vin=vout 这个平衡点点位于约1.40V处,即46.7% VDD处。

尺寸受限情况
如果设计受限,W不能接受太长的尺寸,只能将K值变大,才能满足要求。就变成了以下的式子。
(
W
L
)
p
=
K
(
W
L
)
n
K
>
2
\Big( {W \over L} \Big)_p = K \Big( {W \over L} \Big)_n \newline \enspace \newline K > 2
(
L
W
)
p
=
K
(
L
W
)
n
K
>
2
例如设计以下尺寸,此时K=3。
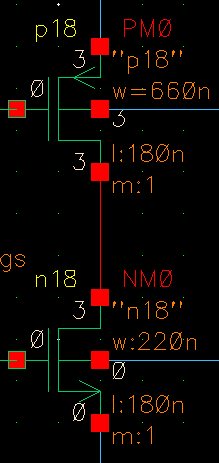
此时,vin=vout 这个平衡点点位于约1.44V处,即48% VDD处。

分析原理
从MOS的V-I特性公式入手。有以下关系,它们的电流相等,同时展开两边的式子。
I
D
S
n
=
I
D
S
p
1
2
K
n
(
W
L
)
n
(
V
G
S
−
V
T
n
)
2
(
1
+
λ
n
V
D
S
)
=
1
2
K
p
(
W
L
)
p
(
V
G
S
−
V
T
p
)
2
(
1
+
λ
p
V
D
S
)
I_{DSn} = I_{DSp} \\\enspace\\ {1 \over 2} K_n \Big( {W \over L} \Big)_n (V_{GS}-V_{Tn})^2 (1+\lambda_nV_{DS}) \\=\\ {1 \over 2} K_p \Big( {W \over L} \Big)_p (V_{GS}-V_{Tp})^2 (1+\lambda_pV_{DS})
I
D
S
n
=
I
D
S
p
2
1
K
n
(
L
W
)
n
(
V
G
S
−
V
T
n
)
2
(
1
+
λ
n
V
D
S
)
=
2
1
K
p
(
L
W
)
p
(
V
G
S
−
V
T
p
)
2
(
1
+
λ
p
V
D
S
)
这里的工艺参数选用的是SMIC 0.18um工艺库参数,在我的上一篇文章中已经计算得出。可以点击下面查看。
用Cadence Virtuoso IC617仿真工艺库参数
在关系式中,VGS = VDS = 0.5*VDD,同时忽略右边部分影响不大的式子,就得出下面的关系式。
(
V
G
S
−
V
T
n
)
2
(
1
+
λ
n
V
D
S
)
=
1.855
(
V
G
S
−
V
T
p
)
2
(
1
+
λ
p
V
D
S
)
=
1.819
∵
1.855
≈
1.819
∴
I
D
S
n
=
I
D
S
p
⟹
K
n
(
W
L
)
n
=
K
p
(
W
L
)
p
(V_{GS}-V_{Tn})^2 (1+\lambda_nV_{DS}) =1.855 \\\enspace\\ (V_{GS}-V_{Tp})^2 (1+\lambda_pV_{DS}) =1.819 \\\enspace\\ \because 1.855 \approx 1.819 \\\enspace\\ \therefore I_{DSn} = I_{DSp} \enspace\Longrightarrow\enspace K_n \Big( {W \over L} \Big)_n = K_p \Big( {W \over L} \Big)_p
(
V
G
S
−
V
T
n
)
2
(
1
+
λ
n
V
D
S
)
=
1
.
8
5
5
(
V
G
S
−
V
T
p
)
2
(
1
+
λ
p
V
D
S
)
=
1
.
8
1
9
∵
1
.
8
5
5
≈
1
.
8
1
9
∴
I
D
S
n
=
I
D
S
p
⟹
K
n
(
L
W
)
n
=
K
p
(
L
W
)
p
也就是说,最后这个关系式,和工艺参数Kn与Kp,以及我们设计的晶体管尺寸比有关。将式子变形,变成比值的形式。
(
W
L
)
p
(
W
L
)
n
=
K
n
K
p
=
K
≈
2.4
{\Big( {W \over L} \Big)_p \over\Big( {W \over L} \Big)_n}={K_n \over K_p}=K\approx2.4
(
L
W
)
n
(
L
W
)
p
=
K
p
K
n
=
K
≈
2
.
4
这个结果和前面得出的结果是一致的,K需要稍微大于2,此时效果最好。
当然,采用不同的工艺(尤其是更先进的工艺),以及VDD改变时,这个K值会有一些细微的变化。
同时,对于模拟电路来说,我们很多设计都是建立在“经验”和“估算”上的,这里所记录的经验能适用于部分情况,但不能适用于所有情况。本节的标题也将其归纳为“经验”而不是“定理”。