
作者:vxbomath
同学们学好函数这个高中数学的枢纽章节函数,对于同学学习其他的章节一定会有很好的帮助,今天老师给大家将函数的三要素的定义域。
定义域是函数的灵魂,我在做题的时候忘掉什么,都不能忘掉定义域;如果忘掉定义域做题的时候就会出现错误的,不管是求函数问题,还是解方程过程一定要记住。定义域是函数的灵魂;不能忘掉。
再解已知解析式型的时候定义域用四个类型能想全面:
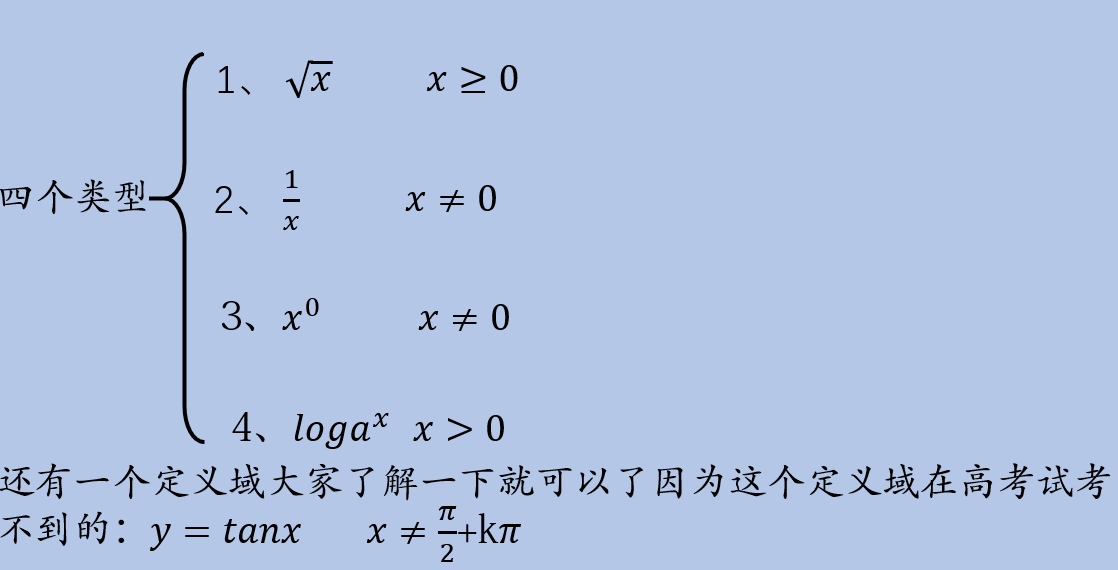
定义域是函数的灵魂这个点大家不要忘,因为这个点并不是考察同学们的学习能力,而是考察同学们细不细心;如果同学们在做函数问题的时候没有条件反射想定域,那么这个点很有可能会出错,这点错后面的点就会跟着错。我们通过一个例题把四个类型都讲一遍;接着看题:
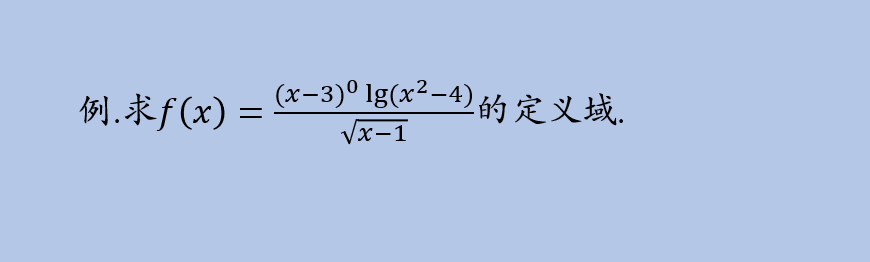
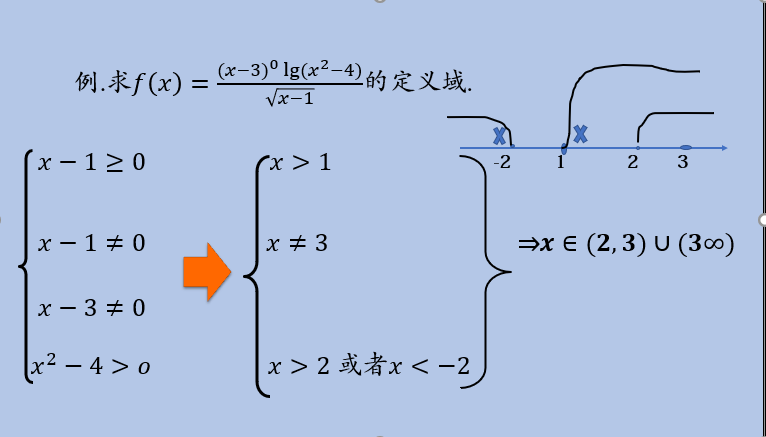
审题:根号下x,x大于等于0,出现了根号,就要强调x减1大于等于0,还要强调x分之1分母不为0,所以x减一不等于0;在强调x的0次幂,x不等于0,这里出现了(x-3)的0次幂,所以x减3不对等于0;最后强调log这里的X被称为真数,所以x的2次幂减4是大于0,这是四个点我们要结合来接题;看1和2是X大于1的,第三个是x不等三的,第四个是x平方大于4写成x大于2或者x小于负二,在去他的交集,我们在取交集的时候由于x不等于3.所以我们不要看它。同学们我要的是每个区间上出现连个线段的部分。这就说明:x属于2到3并3到正无穷大;
接下来我讲抽象函数:
解抽象函数记住这两句话:

这里我们要注意这里的X的本身,这里的本身二字非常重要,第二句里的f()内部的限定是一致的,是被称为解这类题的桥梁;
看题:

审题:已知f(x)的定义域是3到5,说定域就是说X的本身范围。那么求f(2x-1)定义域就是求x本身范围。f(x)的定义域为3到5.我就认为x小于等于5、大于等于3,现在让我们求f(2x-1)的定义域是在求X范围这里我们就要使用桥梁,因为放入f()里的限制是一样的。所以认为2-x也是小于等于5、大于等于3,说明x小于等于3、大于等于;所f(2x-1)的定义域为2到3;

接着看下一题:

审题:已知f(2x-1)的定义域为3到5,求f(x)的定义域;说定义域就是说x的本身。所以x小于等于5、大于等于3;求f(x)的定义域 ,找到f()内部的限制 ,根据已知发现是2x-1放进去了;所以根据X小于等于5、大于等于3;得出2x-1的范围是小于等于9、大于等于5;用桥梁把f(x)的限定放进去,就得到x小于等于9、大于等于5;所以f(x)的定义域为5到9;

接着看下一题:

审题:已知f(2x-1)的定义域是3到5,求f(4x-1)的定义域.说定义域就是说x本身;说明x大于等于3、小于等于5,所以2x-1大于等于5、小于等于9;桥梁是4x减1大于等于5、小于等于9;求定义域就是求X本身范围,所以反解x;x小于等于2分之5、大于等于2分之3,;所以f(4x-1)的定义域为2分之3到2分之5;

接下来讲的是已知定义域求参数范围;

审题;发现这道题含参数K了,它说定义域为R,求k的取值范围,不管x取什么值的时候,根号下面的式子是恒大得0的,遇到这样的题型不管函数、不等式、方程问题只要最高思想含参了;养成好习惯谈论参数是否存在;
假设两种情况:
- k得0,f(x)等于根号1,已知定义域是R,那么x就属于R,x在取什么值得时候都是根号1,所以根号1是成立的;
- k不得0,就是2次式了,这里就认为是二次函数式,会发现有无穷个点使得函数值是小0的。那么这样的函数值放在根号里面是没有意义的;
所以必须要k大于0 ,会发现k大于0也是不成立的;
Delta小于等于0,等于0也是可以,因为根号0,也是有意义;现在来解题k大于0,Delta=k方减4k小于等于0;在解k大于0,k大于等于0、小于4;在取交集所以k大于0、小于等于4;在根据第1第2个点去并集所以k属于0到4;
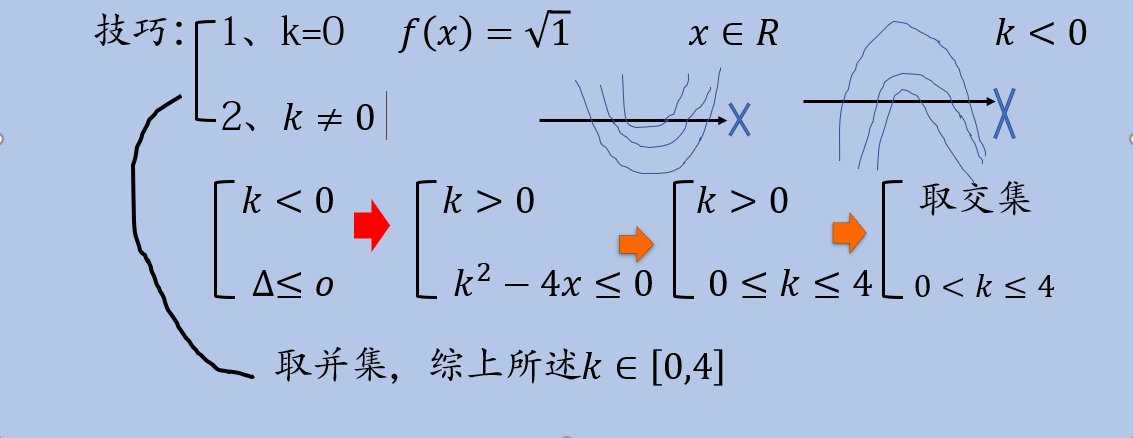
今天的知识就分享到这里,需要更多高质量的解题技巧可以私聊老师,可以评论在下方老师会统一回复大家!