模板持续更新中… …
1 、判断闰年
闰年:能被400整除;或 能被4整除,但不能被100整除。
static boolean is (int x ){
return x%400==0 || (x%4==0 && x%100!=0)
}
2 、 最小公倍数
//least Common Multiple—> lcm
// 两个数比较
static int lcm1(int a,int b){
return a*b/gcd(a,b);
}
static int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
//多个数的最小公倍数
static int lcm2(int [] a){
int n = a.length;
int L = a[0];
for(int i=1;i<n;i++)
L = lcm1(L,a[i]);
return L;
}
3.1 、最大公约数 — 辗转相除法(欧几里得算法)
//Greatest Common Divisor—–> gcd
此算法当 a、b两个整数较大时,做a%b取模运算的性能会比较差。
//求两个数的最大公约数
static int gcd1 (int a,int b){
return b==0?a:gcd1(b,a%b);
}
//求多个数的最大公约数
static int gcd2(int [] a){
int n = a.length;
int L = a[0];
for(int i=1;i<n;i++)
L = gcd1(L,a[i]);
return L;
}
3.2 、最大公约数 — 更相减损术
此方法避免了大整数取模可能出现的性能问题,但当两个数相差较大时(如:2,999990),其运算次数远大于辗转相除法。so,看3.3
static int gcd(int a,int b){
if(a==b)
return a;
int big = a>b ? a : b;
int small = a<b ? a : b;
return gcd(big -small , samll);
}
3.3 、最大公约数 — 更相减损术+移位运算
此模板代码中,判断整数奇偶性的方式是让整数和1进行与运算,如果(a&1)==0,则说明整数a是偶数;如果(a&1)!=0,则说明整数a是奇数。
此算法的基本思路:
#当a和b均为偶数时:
gcd(a,b) = 2 x gcd(a/2 , b/2) = 2 x gcd(a>>1 , b>>1)
#当a为偶数,b为奇数时,gcd(a,b) = gcd(a/2 , b) = gcd(a>>1,b)
#当a为奇数,b为偶数时,gcd(a,b) = gcd(a,b/2)=gcd(a,b>>1)
#当a和b均为奇数时,先利用更相减损术运算一次,gcd(a,b) = gcd(b,a-b),此时 a-b必然是偶数,然后又可以继续进行移位运算。
//GetCommonDivisor
static int gcd(int a,int b){
if(a==b)
return a;
if((a&1)==0 && (n&1)==0){
return gcd(a>>1 , b>>1)<<1 ;
}else if((a&1)==0 && (b&1)!=0){
return gcd(a>>1,b);
}else if((a&1)!=0 && (b&1)==0){
return gcd(a,b>>1);
}else{
int big = a>b ? a : b;
int small = a<b ? a : b;
return gcd(big -small , samll);
}
}
3.4 、 欧几里得算法扩展–裴蜀(贝祖)等式
对任何整数 a,b 和他们的最大公约数d,关于未知数 x和 y的线性丢番图方程(称为裴蜀等式):
ax + by = m 有整数解时,当且仅当m是d的倍数
裴蜀等式 有解时必然有无穷多个整数解,每组解x,y都称为裴蜀数,可用扩展欧几里得算法求得
方程 12x + 42y = 6 有解
特别的, 方程ax+ by =1 有整数解当且仅当 a和b 互素
/**
* 扩展欧几里得
* 调用完成后 x、y是ax + by=gcd(a,b)的解*/
static long x = 0,y = 0;
public static ext_gcd(long a , long b){
if(b==0){
x = 1;
y = 0;
return a;
}
long res = ext_gcd(b,a%b);
long x1 = x; // 备份 x
x = y ; // 更新 x
y = x1 - a/b*y ; // 更新 y
return res;
}
/**
* 线性方程
* ax + by = m 当 m是gcd(a,b)倍数时有解
* 等价于 ax = m mod b */
public static long linearEquation(long a , long b, long m)throws Exception{
long d = ext_gcd(a,b);
// m不是gcd(a,b)的倍数时
if(m % d != 0) throw new Exception("无解");
long n = m / d; //约一下,考虑m是d的倍数
x *= n;
y *= n;
return d;
}
4.1 、筛素数O(n^(3/2))
static boolean is(int n){
if(n==1)
return false;
for(int i=2;i<Math.sqrt(n);i++)
if(n%i==0)
return false;
return true;
}
4.2 、 埃氏筛法-素数
利用数组下标,再依次修改数组是否为素数。
素数定理:1-n的数中的素数个数为: n/logn,用于开数组的大小。
测试得到:该方法求第十万个素数 用时 156ms .
public static long CountPN(int N ){
//N是 第N个素数
//已知在整数x内大概有 x/log(x)个素数
// 以下几行代码 仅为开辟数组空间所用,如果空间足够,直接开Long_MaxValue也可。
int n = 2;
while(n/Math.log(n) < N){
n++;
}
// 开辟一个数组,下标是自然数,值是标记
//基本思路是筛选法,把非素数标记出来
boolean arr[] = new boolean [n];
int x = 2;
while(x<n){
if(arr[x] == true){//true表示不是素数
x++;
continue;
}
// 对每个x,我们从2倍开始,对x的k倍全部标记为-1
int k = 2;
while(x*k < n){
arr[x * k] = true;
k++;
}
x++;
}
// 筛完之后,这个很长的数组里面非素数下标对应的值为 true
int count = 0;
long result = 0;
for(int i=2;i<arr.length;i++){
//是素数 计数+1
if(arr[i] == false){
count++;
}
if(sum == N)
result = i;
}
return result;
}
5 、 进制问题
手工取余法
※ Integer.toString( i , radix ) ; 将i转为radix进制
5.1 、进制(位运算 )问题 — 判断一个整数是否为
2
的整数次幂
如果采用循环,2^n>num时 执行return ,必超时。
如果将左移位代替 for循环中的 乘2 运算,虽会提高性能,但时间复杂度仍为O(logn) , O(1)解法 看下面代码
此方法运用了:2的整数次幂的二进制表示为:第一位为1,其余全为0;2的整数次幂-1的二进制表示:全为1
例 64 —-1000000 | … 63 —-111111
。。 32 —-100000 | … 31—-11111
public static boolean isPowerOf(int num){
return (num & num-1) == 0;
}
5.2 、 进制(位运算 )问题 —- 二进制中1的个数
输入一个整数,输出该数二进制表示中n的个数
n和n-1做一次 与运算,消除一个最低位的1,一次类推
static int count1(int n){
int count = 0;
while( n!= 0){
n = (n-1)&n;
count++;
}
return count;
}
5.3 、 进制(位运算 )问题 —- 将整数的奇偶位互换
整数的二进制位互换
static int m(int n){
int ou = n & 0xaaaaaaaa ; // 和 1010 1010 。。。 做与运算,取出偶数位
int ji = n & 0x55555555 ; // 和 0101 0101 。。。 做与运算,取出奇数为
return (ou>>1) ^ (ji<<1) ; // 异或运算 连起来
}
5.4 、 进制(位运算 )问题 —- 0~1间浮点实数的二进制表示
例:给定一个介于0和1之间的实数,如0.625,类型为double,打印它的二进制表示:0.101
因为小数点后的二进制分别表示为0.5,0.25,0.125…
如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”
整数的10进制转二进制是除以2,小数的是乘2(每次乘2,判断整数位,整数位是1则二进制写1,不足1写0,扣掉整数位,重复)
static String binaryX(int m){
StringBuilder sb = new StringBuilder("0.");
while(m > 0){
//乘2
double r = m*2;
if(r>=1){
sb.append("1");
//消除整数部分
m = r-1;
}else{
sb.append("0");
m = r;
}
if(sb.length()>34){ // 32位二进制,+ 0. 的两位
return "ERROR";
}
}
return sb.toString();
}
5.5 、 进制(位运算 )问题 —- 出现 k 次与出现 1 次
数组中只有一个数出现了1次,其他数都出现了k次,请输出只出现1次的数。
出现k次的数 做不进位的k进制相加为0
//个人忽然感觉有比k进制求解更优的方法,所以那个k进制的破方法就不写了!
//以下为个人思路,题目太简单 其实没有作为模板的意义,可以忽略本题
//时间复杂度 O(n) 空间复杂度O(n)
static int search1(int [] a){
Array.sort(a);
if(a[0]!=a[1] && a[1]==a[2])
return a[0];
if(a[a.length-1] != a[a.length-2] && a[a.length-2] ==a[a.length-3])
return a[a.length-1];
else{
for(int i=1 ;i<a.length-2;i++){
if(a[i]!=a[i-1] && a[i]!=a[i+1])
return a[i];
}
}
return -1;
}
5.6 、 进制(位运算 )问题 —- Nim游戏(此题思维很重要)
一共有N堆石子,编号 1…n ,第i堆中有a[i]个石子
每一次操作Alice和Bob可以从任意一堆石子中取出任意数量的石子,至少取一颗,至多取出这一堆剩下的所有石子。
两人轮流行动,取光所有石子的雅芳获胜。Alice先手
.
给定a,假设两人都采用最优策略,谁会获胜?
// ※ 所有堆的石子数,面临全部异或为0 则输
static boolean solve(int [] a){
int res = 0;
for(int i=0;i<a.length;i++){
res ^= a[i];
}
return res != 0 ;
}
5.7 、 进制(位运算 )问题 —- 阶梯尼姆博弈
5.8 、进制(位运算 )问题 —- 天平称重(蓝桥杯真题)
天平称重:变种三进制
用天平称重时,我们希望用尽可能少的砝码组合称出尽可能多的重量。如果有无限个砝码,但他们的重量分别是 1,3 , 9, 27 ,… …等3的指数幂。神奇之处在于用它们的组合可以称出任意整数重量(砝码允许放在左右两个盘中)。
.
本题目要求编程实现:对用户给定的重量,给出砝码组合方案,重量<1000000
例如:
用户输入
5
程序输出
9-3-1
import java.util.Scanner;
import java.util.List;
public class Main{
public static void main(String [] args){
Scanner in = new Scanner(System.in);
int n = in.nextInt();
//转成3进制
String x = Integer.toString(n,3);
//翻转后,转成字符数组
char[]arr = new StringBuilder(x).reverse().toString().toCharArray();
//放处理之后的 0 -1 1
List<Integer> list = new ArrayList<>();
for(int i=0;i<arr.length;i++){
if(arr[i] == '2'){
list.add(0,-1);// -1插在开头
if(i==arr.length-1){
list.add(0,1); // 最后一个字符,进位
}else{
++arr[i+1]; // 否则,对下一个数字加1
}
}else if(arr[i] == '3'){
list.add(0,0); //插入0
//更高位进1
if(i==arr.length-1){
list.add(0,1);
}else{
++arr[i+1];
}
}else{
list.add(0,arr[i]-'0');
}
}
StringBuilder sb = new StringBuilder();
for(int i=0;i<list.size();i++){
if(list.get(i)==1)
sb.append("+").append((int)Math.pow(3,list.size()-i-1));
if(list.get(i)==-1)
sb.append("-").append((int)Math.pow(3,list.size()-i-1));
}
System.out.Println(sb.subString(1));
}
}
6.1、 子数组最大累加和
给定一个数组arr,返回子数组的最大累加和
例:arr = [1,-2,3,5,-2,6,-1] ; 所有的子数组中[3,5,-2,6]可以累加出
最大的和12,所以返回12
public class Main{
//法一:暴力破解 O(n^2)
static void findByForce(int [] arr){
int maxSum = arr[0];
for(int j=0;j<arr.length;j++){
int sum = arr[j] ;//某个元素为子数组的第一个元素
int maxOfJ = sum;
for(int i=j+1;i<arr.length;i++){
sum+=arr[i];//累加后续元素
if(sum>maxOfJ){
maxOfJ = sum;
}
}
if(maxOfJ>maxSum){
maxSum = maxOfJ;
}
}
System.out.println(maxSum);
}
// 法二: 递推法 O (n)
//※ 单向扫描求和,sum是负数则丢弃,是正数保留
static int findByDp(int [] arr){
int sunJ = arr[0]; //前J个元素的最大贡献
int max = sumJ;
for(int j=1;j<arr.length;j++){
if(sumJ => 0){ //左子表的最大和为正,继续向后加
sumJ += arr[j];
}else{
sumJ = arr[j];
}
if(sumJ > max){
max = sumJ;
}
}
return max;
}
public static void main(String [] args){
int [] arr = {100,-20,55,-79,20,22,73,-35};
findByForce(arr);
System.out.println(findByDp(arr));
}
}
6.2 、 子矩阵最大累加和
给定一个矩阵matrix , 其中的值有正,有负,有0 ,返回子矩阵的最大累加和。
例如,matrix为:
-1 -1 -1
-1 .2 .2
-1 -1 -1
其中最大累加和的子矩阵为: 2 2
所以返回 4
//本题暴力解法不可取,时间复杂度太高
//先按列求和(单行按列--到--所有行按列求和),化为一维数组
//再运用上一题中的递推法,最终比较出最大子矩阵的累加和
import java.util.Scanner;
public class Main{
// O(n^3)
private static int maxSum(int [][] matrix){
int beginRow = 0 ; //以它为起始行
int M = matrix.length;
int N = matrix[0].length;
int [] sums = new int [N]; //按列求和
int max = 0; //历史最大的子矩阵和
while(beginRow < M){ //起始行
for(int i = beginRow ;i<M;i++){ //从起始行到第i行
//按列累加
for(int j=0;j<N;j++){
sums[j]+=matrix[i][j];
}
//累加完成
int t = finByDp(sums); //用到上一题的递推法
if(t > max) max = t;
}
Arrays.fill(sums,0);//快速地将sums的每个元素都设为0
//另起一行作为起始行,把sum清零
beginRow++;
}
return max;
}
public static void main(String [] args){
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int n = in.nextInt();
int [][] a = new int [m][n];
//输入数据代码 略
//竞赛中 尽量考虑边界情况,及矩阵为空,m=n=0,
//执行方法体时,则会出现下标0 越界的情况,也可将此判断语句放在方法体内
if(a.length==0){
System.out.println("0")
}else{
System.out.println(maxSum(a));
}
}
}
7 .、 字符串操作

7.1 、 字符串操作—字符串压缩
字符串压缩问题:将给定的字符串,按照规格压缩,输出压缩后的字符串。压缩规格为:相同字符连续,则压缩为“字符+数字个数”,如”aaaa”压缩为”a4”,srcStr = “aaacccddef” 返回:“a3c3d2ef”
import java.util.Scanner;
public class Main{
public static StringBuffer yasuo(String s) {
int lins = 0 ,n = s.length();
StringBuffer str = new StringBuffer();
for(int i=0;i<n;i+=lins) {
int count = 0;
for(int j=i;j<n;j++) {
if(s.charAt(i)==s.charAt(j))
count++ ;
else
break ;
}
if(count==1)
str.append(s.charAt(i));
else
str.append(s.charAt(i)).append(count);
lins = count;
}
return str;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s1 = in.nextLine();
System.out.println( yasuo(s1) );
}
}
7.2 、 字符串操作— 去除字符串中连续出现的K个字符char
移除字符串中连续出现的k个字符 ch
可以用扫描字符数组的方法,但是用正则表达式更为快捷
static String remove(String str , int k ,char ch){
String regexp = ch+"{"+K+"}";
return str.replaceAll(regexp,"");
}
7.3 、 字符串操作—判断回文字符串
“回文串”是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串。
// 方法一 : 字符逐一比较
static boolean isHuiWen(String str){
int count = 0;
for(int i = 0; i < str.length()/2; i++) {
if((str.substring(i,i+1)).equals(str.substring(str.length() -1-i,str.length()-i))) {
count ++;
}
}
if(count == str.length()/2) {
return true;
}
return false;
}
// 方法二 : 使用StringBuffer/StringBuild 的reverse()方法进行字符串翻转
static boolean isHuiWen(String str){
StringBuilder sb=new StringBuilder(str);
sb.reverse();
String newStr=new String(sb);
if(str.equals(newStr)){
return true;
}
return false;
}
7.4 、 字符串操作—字符串匹配–RabinKarp(上)
O(m*n)
RabinKarp:hash法
- 对目标字符串按d进制求值,mod h 取余作为其 hash
- 对源串,依次求出m个字符的hash ,保存在数组中(滚动计算)
- 匹配时,只需比对目标串的hash值和预存的源串的hash值表
需要匹配的字符串为三个字符时,计算哈希值示例:
( ( 0+A1 ) *31 ) + A2 ) * 31 + A3 = A1 * 31^2 +A2 * 31 + A3
更多字符时同理递推。计算哈希值的方法有很多种,尽量选择不产生重复值的方法
// p为模式串 , s为源串
static void match(String p , String s){
long hash_p = hash(p); // p的hash值
int p_len = p.length();
for(int i=0;i+p_len <= s.length();i++){
long hash_i = hash(s.subString(i,i+p_len));
if(hash_i == hash_p){
if(p == s.substring(i,i+n))//此行代码为了避免hash冲突
System.out.println("match:"+i);
}
}
}
/**
* 使用 100000 个不同字符串产生的冲突数,大概在0~3波动,
* 使用100百万个不同的字符串,冲突数大概110+范围波动
*/
static long seed = 31 ; //求哈希值的一个种子,素数
static long hash(String str){
long hash = 0;
for(int i=0; i != str.length() ; i++){
hash = seed * hash + str.charAt(i);
}
return hash % Long.MAX_VALUE;
}
7.5 、 字符串操作—字符串匹配–RabinKarp(下)
O(2m+n)
RabinKarp:滚动hash法
-计算了前1-3字符的hash 值value1,在计算2-4时的值value2时: value2 = (value1+A4)* 31 – A1* 31^4
此滚动方法降低了时间复杂度
static void match(String p,String s){
long hash_p = hash(p); // p的hash值
long[] hashOfS = hash(s,p.length());
match(hash_p,hashOfS);
}
static void match(long hash_p , long []hash_s){
for(int i=0;i<hash_s.length;i++){
if(hash_s[i] == hash_p ){
if(p == s.substring(i,i+n))//此行代码为了避免hash冲突
System.out.Println("math:"+i)
}
}
}
/**
* n 是子串(模式串)的长度
* 用滚定方法求出s中长度为n的每个子串的hash,组成一个hash数组
*/
static long seed = 31;
static long hash(String str){
long hash = 0;
for(int i=0; i != str.length() ; i++){
hash = seed * hash + str.charAt(i);
}
return hash % Long.MAX_VALUE;
}
static long[] hash(String s,int n){
long[]res = new long[s.length()-n+1];
//前m个字符的hash
res[0] = hash(s.substring(0,n));
for(int i = n;i<s.length();i++){
char newChar = s.charAt(i);
char ochar = s.charAt(i-n);
//前n个字符的hash*seed-前n个字符的第一字符*seed的n次方
long v = (res[i-n]*seed + newChar - (long)Math.pow(seed,n)*ochar) % Long.MAX_VALUE;
if(v<0) v+=Long.MAX_VALUE;
res[i-n+1] = v;
}
return res;
}
7.6 、 字符串操作—字符串匹配–KMP(上)-暴力破解
//如果匹配成功返回 源字符串中对应模式串的第一个字符索引
static int indexOf(String s,Stirng p){
int i = 0;
int sc = i;
int j = 0;
while(sc < s.length()){
if(s.charAt(sc) == p.charAt(j)){
sc++;
j++;
if(j==p.length())
return i;
}else{
i++;
sc = i; //扫描指针以i为起点
j = 0; // j 恢复为0
}
}
return -1;
}
7.6 、 字符串操作—字符串匹配–KMP(下)- next数组
next[ j ] = k —–> j失配,j回溯到K
public class KMP {
private int[][] dp;
private String pat;
public KMP(String pat) {
this.pat = pat;
int M = pat.length();
// dp[状态][字符] = 下个状态
dp = new int[M][256];
// base case
dp[0][pat.charAt(0)] = 1;
// 影子状态 X 初始为 0
int X = 0;
// 构建状态转移图(稍改的更紧凑了)
for (int j = 1; j < M; j++) {
for (int c = 0; c < 256; c++) {
dp[j][c] = dp[X][c];
dp[j][pat.charAt(j)] = j + 1;
// 更新影子状态
X = dp[X][pat.charAt(j)];
}
}
public int search(String txt) {
int M = pat.length();
int N = txt.length();
// pat 的初始态为 0
int j = 0;
for (int i = 0; i < N; i++) {
// 计算 pat 的下一个状态
j = dp[j][txt.charAt(i)];
// 到达终止态,返回结果
if (j == M) return i - M + 1;
}
// 没到达终止态,匹配失败
return -1;
}
}
7.7 、 字符串操作—字符串匹配–后缀数组
7.8 、 字符串操作—字符串匹配–前缀树(字典树)
8.1 、 快速幂运算– a的n次方(上)
以最快的速度求a的n次方
O(logn)
例:
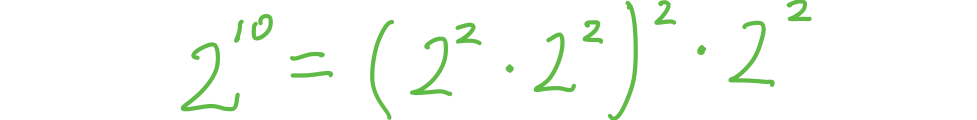
public static int ex(int a ,int n){
if(n==1)
return a;
int temp = a; //a的一次方
int res = 1;
int exponent = 1;
while((exponent << 1) <n){
temp = temp * temp ;
exponent = exponent<<1;
}
res *= ex(a, n-exponent);
return res * temp;
}
8.2 、快速幂运算 – n的m次方(下)巧算
public static long ex2(long n , long m){
long pingfangshu = n ; //n的1次方
long result = 1 ;
while( m != 0){
// 遇1累乘现在的幂
if((m&1)==1)
result *= pingfangshu;
//每移一位,幂累乘方一次
pingfangshu *= pingfangshu ;
// 右移一位
m >>= 1;
}
return result;
}
8.3 、 快速幂运算 – 矩阵幂运算
因为矩阵快速幂运算会用到矩阵相乘,所以放在了9.3
9.1 、 矩阵相乘–方阵
static int[][] multiply(int[][] a,int[][] b){
int n = a.length;
int[][] ans = new int[n][n];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
for(int k=0;k<n;k++)
ans[i][j] += a[i][k]*a[k][j];
return ans;
}
9.2 、 矩阵相乘–一般矩阵
static long[][] multiply(long [][] m1,long [][] m2){
int m1Row = m1.length;
int m1Line = m1[0].length;
if(m1Line != m2.length) throw new IllArgumentException();
int m2Line = m2[0].length;
//新矩阵的行数为m1的行,列数为m2的列数
long[][] result = new long[m1.row][m2.Line];
for(int i=0;i<m1Row;i++){
for(j=0;j<m2Line;j++){
for(int k=0;k<m1Line;k++){
result[i][j] += m1[i][k]*m2[k][j]
}
}
}
return result;
}
9.3 矩阵相乘 – 矩阵快速幂运算
//求矩阵m的p次方
public static long[][] matrixPower(long[][] matrix , long p){
//初始化结果为单位矩阵,对角线为1
long[][] result = new long[matrix.length][matrix[0].length];
//单位矩阵相当于整数1
for(int i =0;i<result.length;i++){
result[i][i] = 1;
}
// 平方数
long[][] pingfang = matrix; // 一次方
while(p !=0){
if((p & 1) !=0){//当前二进制位的最低位为1 ,将当前平方数乘到结果中
result = multiply(result,pingfang);
}
//平方数继续上翻
pingfang = multiply(pingfnag,pingfang);
p>>=1;
}
return result;
}
10.1 、 01背包
f[v]=max{f[v],f[v-c[i]]+w[j]}此状态转移方程,将原来的二维数组变为一维数组。降低了空间复杂的,之所以一维数组也能得到结果,是因为通过一维数组的循环存入数据得到的。对二维数组而言,调用数组左上方的数据。而一维数组通过双重循环,外层正序,内层逆序的原则,使要用到的数据 已经存储在一维数组 当前索引的左侧。
import java.util.Scanner;
public class 01backpack{
public static void main(String [] args){
Scanner in = new Scanner(System.in);
int m = in.nextInt();//大小
int n = in.nextInt();//物品数
int [] dp = new int [m+1];//开背包质量的大小
for(int i=1;i<=n;i++){
int v = in.nextInt(); //物品体积
int w = in.nextInt(); //物品价值
for(int j=m;j>=v;j--)
dp[j] = Math.max(dp[j],dp[j-v]+w);
}
System.out.println(dp[m]);
}
}
10.2 、完全背包
import java.util.Scanner;
public class FullBackpack{
public static void main(String [] args){
Scanner in = new Scanner(System.in);
int m = in.nextInt();//大小
int n = in.nextInt();//物品数
int [] dp = new int [m+1];//开背包质量的大小
for(int i=1;i<=n;i++){
int v = in.nextInt(); //物品体积
int w = in.nextInt(); //物品价值
for(int j=v;j<=m;j++)
dp[j] = Math.max(dp[j],dp[j-v]+w);
}
System.out.println(dp[m]);
}
}