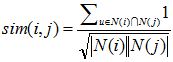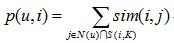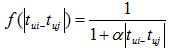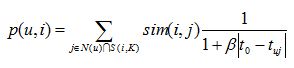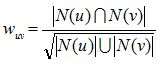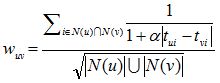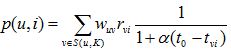本节首先介绍各种不同的时间效应,然后研究如何将这些时间效应建模到推荐系统的模型中,最后通过实际数据集对比不同模型的效果。
1. 时间效应
时间信息对用户兴趣的影响表现在以下几个方面:用户兴趣是变化的;物品也是有生命周期的;季节效应。在给定时间信息后,推荐系统从一个静态系统变成了一个时变的系统,而用户行为数据也变成了时间序列。包含时间信息的用户行为数据集由一系列三元组构成,其中每个三元组(u,i,t)代表了用户u在时刻t对物品i产生过行为。
实现推荐系统的实时性除了对用户行为的存取有实时性要求,还要求推荐算法本身具有实时性,而推荐算法本身的实时性意味着:(1)实时推荐系统不能每天都给所有用户离线计算推荐结果,然后在线展示昨天计算出来的结果。所以,要求在每个用户访问推荐系统时,都根据用户这个时间点前的行为实时计算推荐列表。(2)推荐算法需要平衡考虑用户的近期行为和长期行为,即要让推荐列表反应出用户近期行为所体现的兴趣变化,又不能让推荐列表完全受用户近期行为的影响,要保证推荐列表对用户兴趣预测的延续性。
推荐系统每天推荐结果的变化程度被定义为推荐系统的时间多样性。时间多样性高的推荐系统中用户会经常看到不同的推荐结果。提高推荐结果的时间多样性需要分两步解决:首先,需要保证推荐系统能够在用户有了新的行为后及时调整推荐结果,使推荐结果满足用户最近的兴趣;其次,需要保证推荐系统在用户没有新的行为时也能够经常变化一下结果,具有一定的时间多样性。
2. 时间上下文推荐算法
(1)最近最热门
在没有时间信息的数据集中,我们可以给用户推荐历史上最热门的物品。那么在获得用户行为的时间信息后,最简单的非个性化推荐算法就是给用户推荐最近最热门的物品了。给定时间T,物品i最近的流行度ni(T)可以定义为如下,其中,α是时间衰减参数。
(2)时间上下文相关的ItemCF算法
首先回顾一下前面提到的基于物品的协同过滤算法,它通过sim(i,j)计算物品的相似度:而在给用户u做推荐时,通过p(u,i)计算用户u对物品i的兴趣。
在得到时间信息(用户对物品产生行为的时间)后,我们可以通过如下公式改进相似度计算和修正预测公式。
上面的sim(i,j)中引入了和时间有关的衰减项f(|t(ui)-t(uj)|),其中 t(ui) 是用户u对物品i产生行为的时间。f函数的含义是,用户对物品i和物品j产生行为的时间越远,则f函数值越小。其中衰减函数的选择如上。alpha是时间衰减参数,它的取值在不同系统中不同。如果一个系统用户兴趣变化很快,就应该取比较大的alpha,反之需要取比较小的alpha 。p(u,i)中,t0是当前时间,公式表明,t(uj)越靠近 t0,和物品j相似的物品就会在用户u的推荐列表中获得越高的排名。beta是时间衰减参数,需要根据不同的数据集选择合适的值。上面的推荐算法可以通过如下代码实现。
def ItemSimilarity(train, alpha):
#calculate co-rated users between items
C = dict()
N = dict()
for u, items in train.items():
for i,tui in items.items():
N[i] += 1
for j,tuj in items.items():
if i == j:
continue
C[i][j] += 1 / (1 + alpha * abs(tui - tuj))
#calculate finial similarity matrix W
W = dict()
for i,related_items in C.items():
for j, cij in related_items.items():
W[u][v] = cij / math.sqrt(N[i] * N[j])
return Wdef Recommendation(train, user_id, W, K, t0):
rank = dict()
ru = train[user_id]
for i,pi in ru.items():
for j, wj in sorted(W[i].items(), key=itemgetter(1), reverse=True)[0:K]:
if j,tuj in ru.items():
continue
rank[j] += pi * wj / (1 + alpha * (t0 - tuj))
return rank
(3)时间上下文相关的UserCF算法
UserCF通过如下w(uv)计算用户u和用户v的兴趣相似度,其中N(u)是用户u喜欢的物品集合,N(v)是用户v喜欢的物品集合。在得到用户相似度后,UserCF通过p(u,i)预测用户对物品的兴趣:
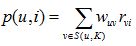
考虑到时间信息后,w(uv)和p(u,i)改进为如下。用户u和用户v对物品i产生行为的时间越远,那么这两个用户的兴趣相似度就会越小。
def UserSimilarity(train):
# build inverse table for item_users
item_users = dict()
for u, items in train.items():
for i,tui in items.items():
if i not in item_users:
item_users[i] = dict()
item_users[i][u] = tui
#calculate co-rated items between users
C = dict()
N = dict()
for i, users in item_users.items():
for u,tui in users.items():
N[u] += 1
for v,tvi in users.items():
if u == v:
continue
C[u][v] += 1 / (1 + alpha * abs(tui - tvi))
#calculate finial similarity matrix W
W = dict()
for u, related_users in C.items():
for v, cuv in related_users.items():
W[u][v] = cuv / math.sqrt(N[u] * N[v])
return Wdef Recommend(user, T, train, W):
rank = dict()
interacted_items = train[user]
for v, wuv in sorted(W[u].items, key=itemgetter(1), reverse=True)[0:K]:
for i, tvi in train[v].items:
if i in interacted_items:
#we should filter items user interacted before
continue
rank[i] += wuv / (1 + alpha * (T - tvi))
return rank