定义

给定一张图，图中有许多的节点还有许多长度不同的边将这些点点相互连接（

连通网

），找出连接所有点的最短方式就是最小生成树，可以证明，这样一种最小的情况是不会出现环的，由于所有的无环图都可以看作树，所以成为最小生成树。

解决问题类型

因为是求最小的，一般是修路问题（代价最小且连接所有点）。

基本算法

1、Prime算法—“加点法”

主要步骤：


1.将图保存邻接矩阵之中（便于访问是否邻接）；

2.任选一点作为起始点；

3.将此点加入到已确定点集之中；

4.依此点为原点，更新与之相关联的节点到点集的距离（最小）；

5. 选中剩余点中距离点集最近的点，加入点集，并以其为原点更新和他相邻接的点的距离；

6. 循环，直到点集中有n个点为止。

图形表示：


以下来源为这位大大（通俗易懂）

原图为：

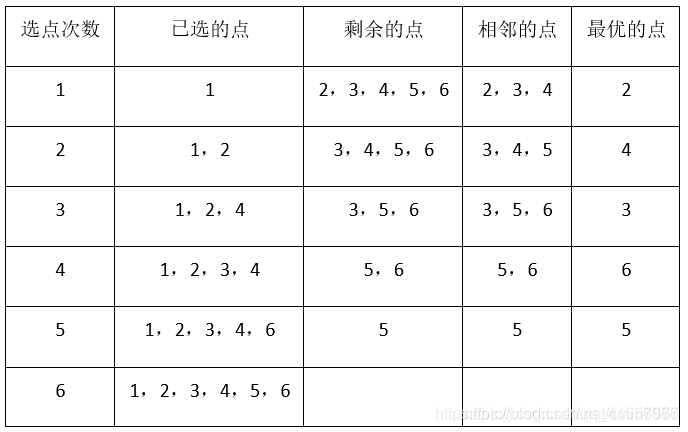
1.首先先找一个点，把这个点看成一个集合

2.找与这个点最近的一个点，也就是找与这个集合最近的一个点，由图可知与1点相邻的有2，3，4三个点，但最近的是2点，并且2点没在已选的集合中，所以把2点加到已选的集合中。



3.现在1和2是在已选的集合中，然后再找与已选集合最近的点，其中相邻的有3，4，5三个点，但最近的只有点4，所以把4点加到已选集合中。

4.然后再找与已选集合最近的点，以此类推下个点为3

6.再下个点为6

7.最后一个点为5，选完所有点后结束

（经过六个图形描述，最后一个自己动手画吧~~~）

2、Kruskal算法—“加边法”

算法思路：


（1）将图中的所有边都去掉。

（2）将边按权值从小到大的顺序添加到图中，保证添加的过程中不会形成环

（3）重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

主要步骤：


1.将图保存在临接矩阵之中（便于访问是否邻接）；

2先把所有的路径进行排序；

3.先选一天路径最小的边然后判断这两个点是否在同一个集合中，如果没有就把这两个点加到一个集合中；

4.然后依次找路径最小的边，并判断这条边上的两个点是否在同一个集合中，如果没在同一个集合中且这两个点没有都被标记过，就把这两个点合到同一个集合中；

5.循环来找，直到点找完为止。

图形表示：

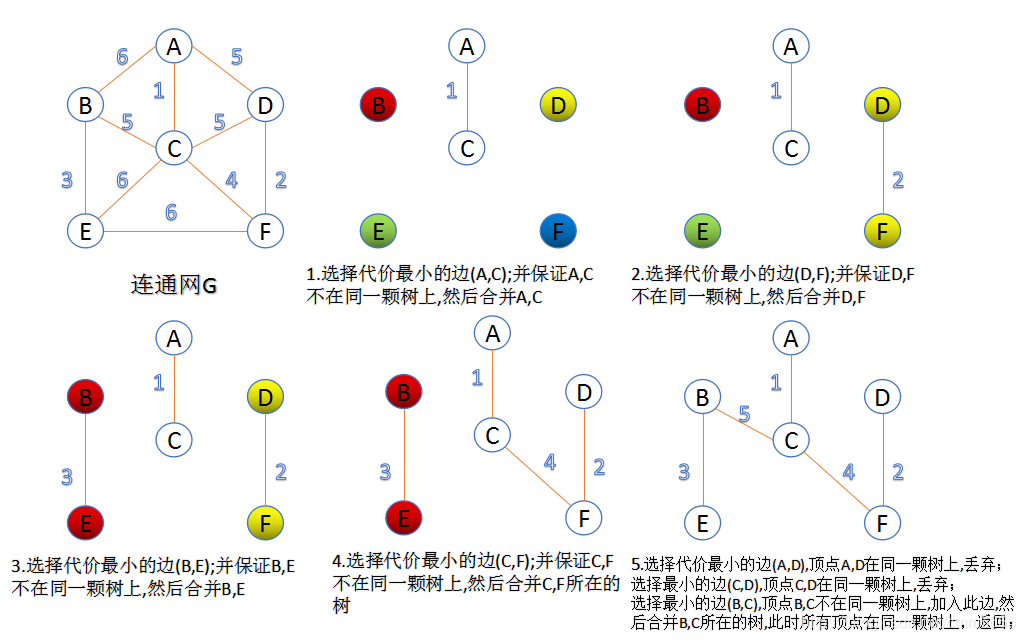
代码（2个）：

/************************************************************************
CSDN 勿在浮沙筑高台 http://blog.csdn.net/luoshixian099算法导论--最小生成树（Prim、Kruskal）2016年7月14日
************************************************************************/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INFINITE 0xFFFFFFFF   
#define VertexData unsigned int  //顶点数据
#define UINT  unsigned int
#define vexCounts 6  //顶点数量
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node 
{
    VertexData data;
    unsigned int lowestcost;
}closedge[vexCounts]; //Prim算法中的辅助信息
typedef struct 
{
    VertexData u;
    VertexData v;
    unsigned int cost;  //边的代价
}Arc;  //原始图的边信息
void AdjMatrix(unsigned int adjMat[][vexCounts])  //邻接矩阵表示法
{
    for (int i = 0; i < vexCounts; i++)   //初始化邻接矩阵
        for (int j = 0; j < vexCounts; j++)
        {
            adjMat[i][j] = INFINITE;
        }
    adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge)  //返回最小代价边
{
    unsigned int min = INFINITE;
    int index = -1;
    for (int i = 0; i < vexCounts;i++)
    {
        if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
        {
            min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
    for (int i = 0; i < vexCounts;i++)
    {
        closedge[i].lowestcost = INFINITE;
    }      
    closedge[s].data = s;      //从顶点s开始
    closedge[s].lowestcost = 0;
    for (int i = 0; i < vexCounts;i++)  //初始化辅助数组
    {
        if (i != s)
        {
            closedge[i].data = s;
            closedge[i].lowestcost = adjMat[s][i];
        }
    }
    for (int e = 1; e <= vexCounts -1; e++)  //n-1条边时退出
    {
        int k = Minmum(closedge);  //选择最小代价边
        cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成树
        closedge[k].lowestcost = 0; //代价置为0
        for (int i = 0; i < vexCounts;i++)  //更新v中顶点最小代价边信息
        {
            if ( adjMat[k][i] < closedge[i].lowestcost)
            {
                closedge[i].data = k;
                closedge[i].lowestcost = adjMat[k][i];
            }
        }
    }
}
void ReadArc(unsigned int  adjMat[][vexCounts],vector<Arc> &vertexArc) //保存图的边代价信息
{
    Arc * temp = NULL;
    for (unsigned int i = 0; i < vexCounts;i++)
    {
        for (unsigned int j = 0; j < i; j++)
        {
            if (adjMat[i][j]!=INFINITE)
            {
                temp = new Arc;
                temp->u = i;
                temp->v = j;
                temp->cost = adjMat[i][j];
                vertexArc.push_back(*temp);
            }
        }
    }
}
bool compare(Arc  A, Arc  B)
{
    return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //检查u,v分别属于哪颗树
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }
 
    if (index_u != index_v)   //u,v不在一颗树上，合并两颗树
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
    vector<Arc> vertexArc;
    ReadArc(adjMat, vertexArc);//读取边信息
    sort(vertexArc.begin(), vertexArc.end(), compare);//边按从小到大排序
    vector<vector<VertexData> > Tree(vexCounts); //6棵独立树
    for (unsigned int i = 0; i < vexCounts; i++)
    {
        Tree[i].push_back(i);  //初始化6棵独立树的信息
    }
    for (unsigned int i = 0; i < vertexArc.size(); i++)//依次从小到大取最小代价边
    {
        VertexData u = vertexArc[i].u;  
        VertexData v = vertexArc[i].v;
        if (FindTree(u, v, Tree))//检查此边的两个顶点是否在一颗树内
        {
            cout << vextex[u] << "---" << vextex[v] << endl;//把此边加入到最小生成树中
        }   
    }
}
 
int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);   //邻接矩阵
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0); //Prim算法，从顶点0开始.
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal算法
    return 0;
}