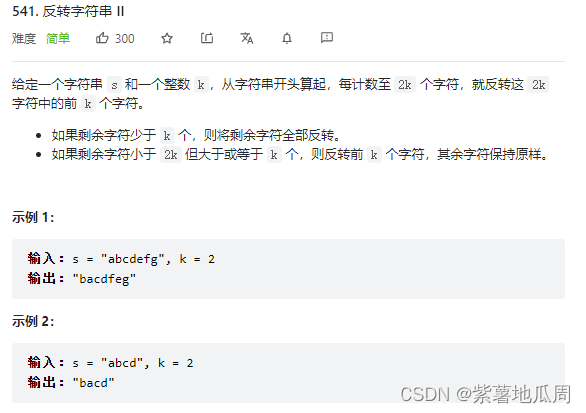
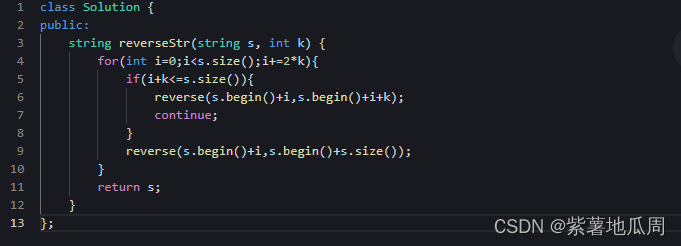
一、反转字符串
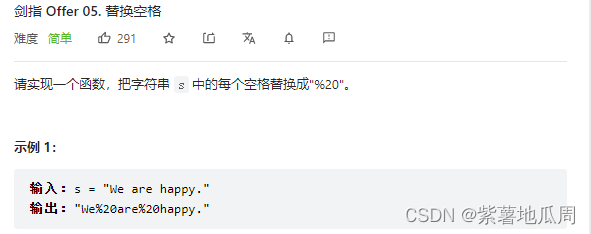
二、替换空格
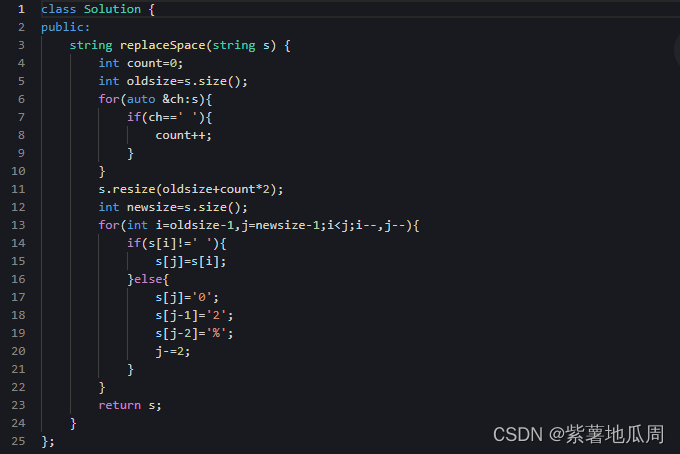
替换空格以后,字符串所占的长度会比原字符串多,所以我们首先需要扩充数组到每个空格替换成“%20”之后的大小。然后从后向前替换空格,(双指针法)
一个指针指向新长度的末尾,一个指针指向旧长度的末尾
之所以选择从后向前,是因为从前向后填充是O(n^2)的算法,因为每次添加元素都要将添加元素之后的所有元素向后移动。
注:很多数组填充类的问题,都可以预先给数组扩容到填充后的大小,然后再从后向前进行操作。
1)不用申请新的数组。
2)从后向前填充元素,避免了从前向后填充元素造成的每次添加元素都要将添加元素之后的所有元素向后移动。
三、颠倒字符串中的单词
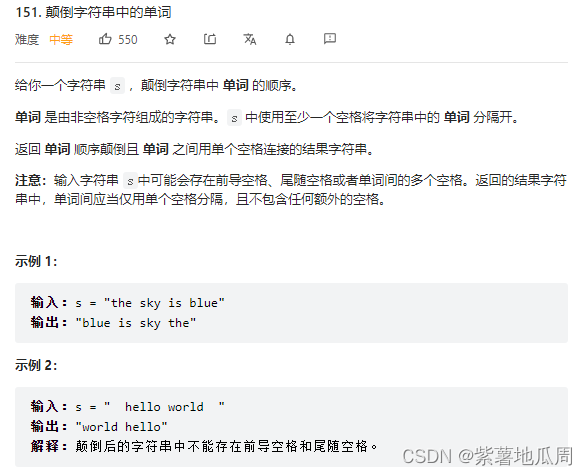
要求空间复杂度O(1)
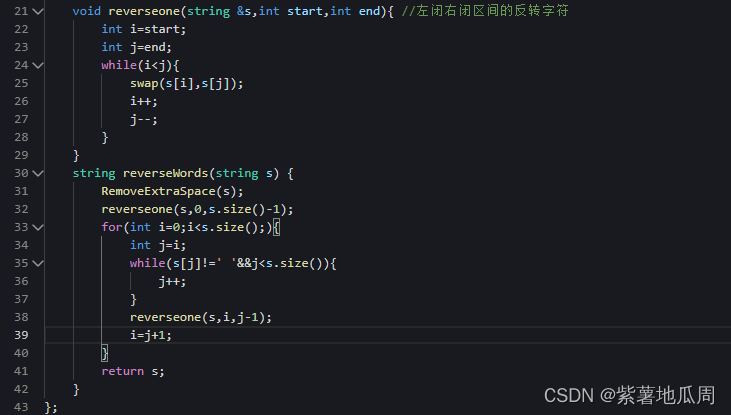
先将整个字符串反转,这样单词的以及单词本身都会是倒序的状态,再将单词反转,就可以得到结果
步骤如下:
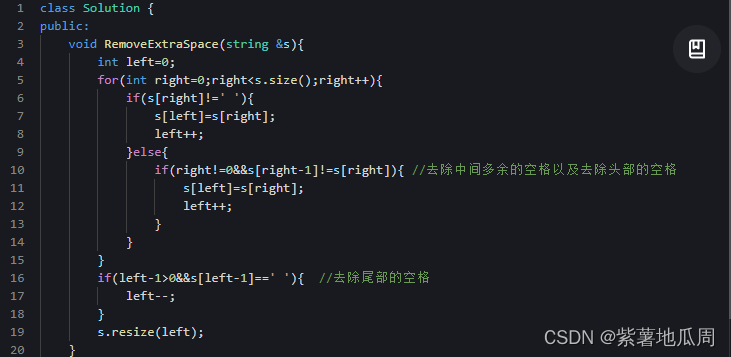
1)移除多余的空格,包括头尾以及中间多的
2)将整个字符串反转
3)将每个单词反转
示例,设一个s为“ the sky is blue ”
跟据上述步骤即 “the sky is blue”->”eulb si yks eht”->”blue is sky the”
四、左旋转字符串
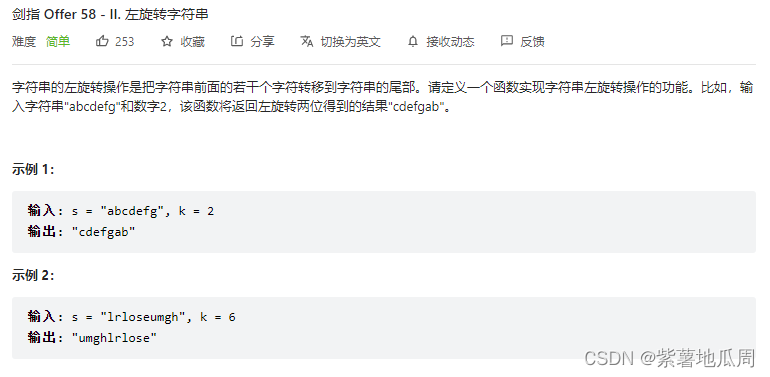
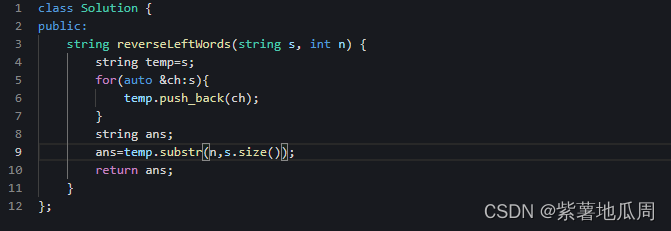
方法一:申请额外空间,利用辅助字符串操作
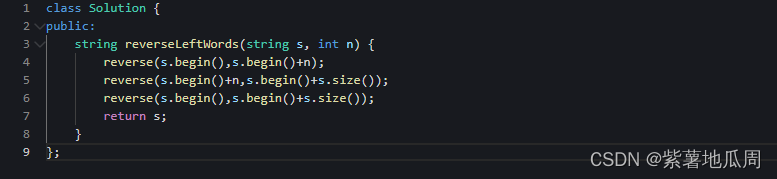
方法二:不申请额外空间,只在本串上操作
可以通过局部反转+整体反转达到左旋转的目的
1)反转区间为前n的子串
2)反转区间为n到末尾的子尾
3)反转整个字符串
最后就可以得到左旋n的目的,而不用定义新的字符串。
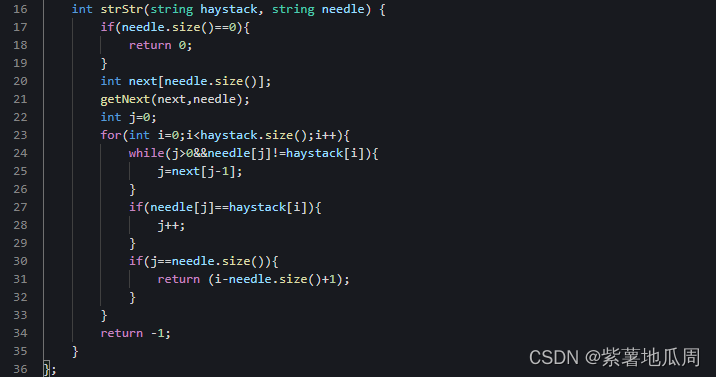
五、实现strStr()
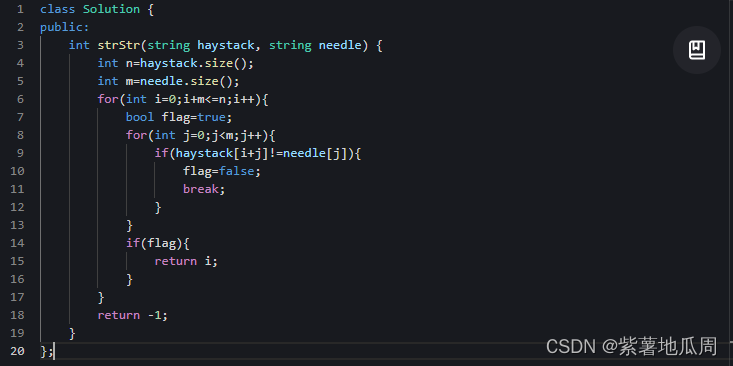
方法一:暴力求解
让字符串 needle 与字符串 haystack 的所有长度为 m 的子串均匹配一次。
为了减少不必要的匹配,每次匹配失败即立刻停止当前子串的匹配,对下一个子串继续匹配。如果当前子串匹配成功,返回当前子串的开始位置即可。如果所有子串都匹配失败,则返回 −1。
方法二:
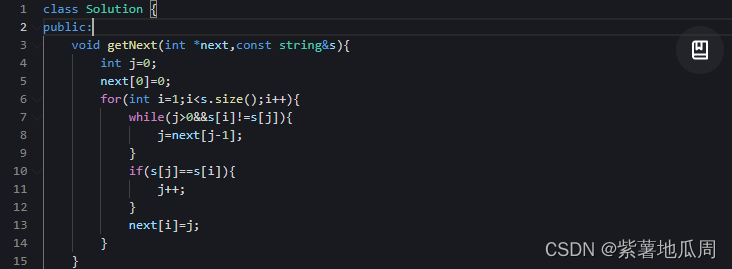
KMP算法
构造next数组
其实就是计算模式串s,前缀表的过程
1)初始化 (定义两个指针i,j,j指向前缀末尾位置,i指向后缀末尾位置)
2)处理前后缀不相同的情况(next[j]记录着j(包括j)之前的字串的相同前后缀的长度。当s[i]和s[j]不相同的时候,就要找j前一个元素在next数组里的值,即next[j-1])
3)处理前后缀相同的情况 (j指针指向位置加一,相等前后缀长度加一)
六、重复的子字符串(KMP)

这也是一道KMP算法的题,KMP算法中的next数组记录的就是最长相同前后缀,记录数组长度为len,当next[len-1]!=-1,则说明字符串有最长相同前后缀(就是字符串里的前缀子串和后缀子串的最长长度)。最长相等前后缀的长度为:next[len-1]。
如果len%(len-next[len-1])==0,则说明(数组长度-最长相等前后缀的长度)正好可以被数组的长度整除,说明该字符串有重复的子字符串。
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度,也就是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。

next[len – 1] = 8,8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
(len – (next[len – 1])) 也就是: 12(字符串的长度) – 8(最长公共前后缀的长度) = 4, 4正好可以被 12(字符串的长度) 整除,所以说明有重复的子字符串(asdf)。
