博客

多分类学习任务经常被划分为多个二分类学习任务，最后进行结果集成完成分类，一般有三种划分方法，“一对一”、“一对其余”、“多对多”(针对类别)。

ECOC(Error Correcting Output Codes,纠错输出码)作为输出表示，用于多分类学习任务。主要思想是，通过事先分别为








k










$k$
类类别定义一串编码序列(code word)。在分类的时候，只需比较待分类样本与各串编码的差异程度(distance measure)。如下图，在Dietterich一文中，一般对于ECOC的大部分应用，其Code Word的每一位都有实际的含义，假设有一预分类样本为110001，则由Hamming distance距离可得，Class 4的距离最小，因此将其划分为Class 4。ECOC还有一个显著的优点就是能够纠错，若最小Hamming distance为d，则ECOC最少能纠正









⌊









d




−


1










2

















⌋











$\lfloor {{d-1}\over{2}} \rfloor$
位的错误(即仍然将其划分为实际正确的类)。

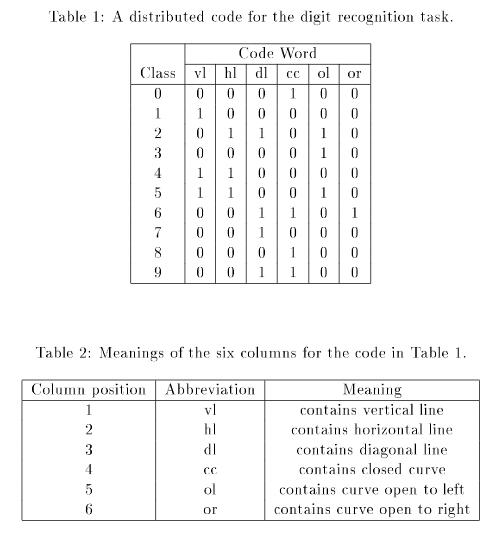
这里就有两个问题，各类的编码序列如何获得，差异程度如何定义。

ECOC编码设计

如先前的例子所示，我们需要构建一个矩阵，行表示一类样本的编码，列则表示一类特征。因此好的ECOC编码应该满足一下两个特征

1.Row separation.对于Hamming Distance，每个编码序列应该与其它编码良好可分。

2.Column separation.每一位编码应该与其余位置的编码不相关。这个可以通过该列与其余列以及其余列的补集的Hamming Distance达到很大来保证。

ECOC编码的纠错能力与Row separation直接相关，每一位编码应该与其余位置的编码不相关，这样ECOC才能工作良好，同时同一时刻多个不同位置发生错误的概率就会很低。如果出现这一情况，则ECOC不再能纠正它们。


同时如果两列编码互补，则其Hamming Distance达到最大，但这时这两列也是高度相关的，这是因为类似C4.5和后向传播算法会将一个类别编码及其互补的编码作为对称的一类，因此需要避免完全相同，但是也不能相互互补。


Dietterich一文中介绍了四种构造ECOC编码的方法。

Exhausive Codes(EC)

当








3


≤


k


≤


7










$3\le k \le 7$
时，我们构建一个长度为








(





2








k


−


1









−


1


)










$(2^{k-1}-1)$
的编码序列。并且如下构建，第一行全部为1，第二行前








(





2








k


−


2









)










$(2^{k-2})$
个0，后面剩余的








(





2








k


−


2









−


1


)










$(2^{k-2}-1)$
为1。第三行依次包含包含








(





2








k


−


3









)










$(2^{k-3})$
个0、








(





2








k


−


3









)










$(2^{k-3})$
个1、








(





2








k


−


3









)










$(2^{k-3})$
个0、








(





2








k


−


3









−


1


)










$(2^{k-3}-1)$
个1。在第








i










$i$
行









(





2








k


−


i









)











$(2^{k-i})$
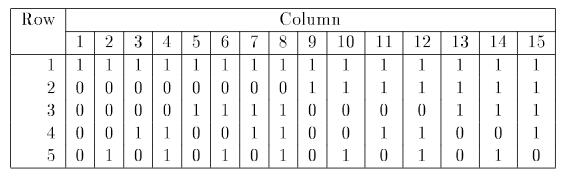
个0、1交替出现。下图为








k


=


5










$k =5$
的示例。

Column Selection From Exhausive Codes(CSEC)

当








8


≤


k


≤


11










$8\le k \le 11$
时，我们依然构建Exhausive Codes，然后在它的列中选择好的子集。使用改进的GSAT算法(

A New Method for Solving Hard Satisfiability Problems

)。

Randomized Hill Climbing

当








k


>


11










$k \gt 11$
时，使用随机搜索算法来得到期望长度为








L










$L$
的









k











$k$
个随机编码序列。

BCH Codes

当








k


>


11










$k \gt 11$
时，我们也可以使用BCH算法来设计编码(

On a class of error correcting binary group codes

&

Codes correcteurs d’erreurs

)。

参考资料：1.Thomas G.Dietterich，Ghulum Bakiri，1995，

Solving Multiclass Learning Problems via Error-Correcting Output Codes


2.周志华，P63-66，《机器学习》

本作品采用

知识共享署名-非商业性使用-相同方式共享 3.0 中国大陆许可协议

进行许可。