博客

看前先看右边界情况

原理

假设目标值在闭区间[l, r]中， 每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

代码模板

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (array(mid)<=target) l = mid;
        else r = mid - 1;
    }
    return l;
}

为什么相较于左边界的模板这里的mid要多加1

如下图情况，数组为A,目标值为0。

初始时，L=0,R=1,mid=(L+R)/2=0;

因为mid指向目标所以L依旧不动，因此L,R的位置永远不会改变，陷入死循环。



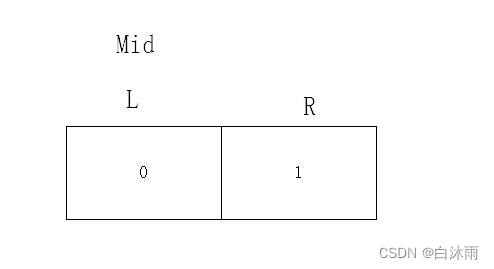
当mid=(L+R+1)/2=1时就不会陷入死循环。L=R退出循环

为什么要等于号放在小于上

和左边界情况类似，为了当mid等于目标值时保留mid右边的数组，因为右边界不可能在mid左边

当目标值不在是l指向第一个比目标值小的值的下标(目标值在最大值和最小值之间）

目标值小于最小值l指向最小值的下标

目标值大于最大值l指向最大值的下标

查找左右边界例题

//AC代码
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
      if(!nums.size())return{-1,-1} ;
       vector<int>s(2);
       s[0]=left_find( nums, target);
       s[1]=right_find( nums, target);
       return s;


    }

    int left_find(vector<int>& nums, int target){
        // 查找左边界
        int l =0,r=nums.size()-1;
        while(l<r){
            int mid=l+r>>1;
            if(nums[mid]>=target)r=mid;
            else l=mid+1;
        }
        cout<<l<<endl;
        if(nums[l]!=target)return -1;
        return l;
    }

    int right_find(vector<int>& nums, int target){
        // 查找右边界
        int l =0,r=nums.size()-1;
        while(l<r){
            int mid=l+r+1>>1;
            if(nums[mid]<=target)l=mid;
            else r=mid-1;
        }
        if(nums[l]!=target)return -1;
        return l;
    }
};