数据结构-线性表的基本操作

本文介绍我在学习数据结构的过程中如何利用线性表编写算法解决实际问题的方法

一、线性表

线性表是最基本、最简单、也是最常用的一种数据结构。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。

二、带头结点的单链表存储

编写一个Java语言程序，实现带头结点的单链表存储及基本操作，要求依次实现单链表插入、删除、追加、查找、取元素、判空、求长度等

（1）声明单链表结点类

public class Node<T>{
    public T data;                               //数据域，存储数据元素
    public Node<T> next;                         //地址域，引用后继结点

    public Node(T data, Node<T> next){
            //构造结点，data指定数据元素，next指定后继结点
        this.data = data;                        //T对象引用赋值
        this.next = next;                        //Node<T>对象引用赋值
    }
    public Node() {
        this(null, null);
    }
    public String toString(){                    //返回结点数据域的描述字符串
       return this.data.toString();
    }
}

（2）编写单链表存取数据，加入插入、删除、追加、查找、取元素、判空、求长度等操作代码

public class SinglyList<T> extends Object {
	public Node<T>head;
public SinglyList() {
		this.head=new Node<T>();
	}
	public SinglyList(T[] values) {//尾插法创建单链表，数组提供元素
		this();//创建只有头节点的单链表
		Node<T>rear=this.head;
		for(int i=0;i<values.length;i++) {
			rear.next=new Node<T>(values[i],null);//尾插法
			rear=rear.next;//指向新的尾结点
		}
	}
	public boolean isEmpty() {//判断单链表是否为空
		return this.head.next==null;
	}

	//存取
	public T get(int i) {//获取值，若i越界，返回null
		Node<T>p=this.head.next;
		for(int j=0;p!=null&&j<i;j++)
			p=p.next;//若p指向i，返回其data值
				return(i>=0&&p!=null)?p.data:null;
	}

	public void set(int i,T x) {//设置第i个元素为x
	int j=0;
	Node<T>p=this.head.next;
	for(i=0;p!=null&&j<i;j++) {//遍历单链表，寻找结点
		p=p.next;
	}
	if(i>=0&&p!=null) {
		p.data=x;
	}
	}

	public int size() {//返回单链表长度
		int len=0;
		Node tmp=head;
		while(tmp!=null) {
			len++;
			tmp=tmp.next;
		}
		return len;
	}
	  
	public String toString() {//返回单链表所有元素的描述字符，形式为"(,)"，覆盖Object类的toString方法
		String str=this.getClass().getName()+"(";
		for(Node<T>p=this.head.next; p!=null;p=p.next) {
			str+=p.data.toString();
			if(p.next!=null)
				str+=",";
		}return str+")";
		}

	    
	//插入
	public Node<T>insert(int i,T x){
		if(x==null)
			throw new NullPointerException("x==null");
		Node<T>front=this.head;
		for(int j=0;front.next!=null&&j<i;j++)
			front=front.next;
		front.next=new Node<T>(x,front.next);
		return front.next;
	}
	public Node<T>insert(T x){
		return insert(Integer.MAX_VALUE,x);
	}

	//删除
	public T remove(int i) {
		Node<T>front=this.head;
		for(int j=0;front.next!=null&&j<i;j++)
			front=front.next;
		if(i>=0&&front.next!=null) {
			T old =front.next.data;
			return old;
		}
		return null;
	}
	public void clear() {
		this.head.next=null;
	}
	
		public boolean contains(T key) {//判断单链表中是否包含key元素
		Node<T> p=this.head.next;
		for(;p!=null;p=p.next) {
			if(p.data.equals(key)) {
				return true;
			}
		}
		return false;
	}

	    public Node<T> search(T key) {                              //功能及参数：返回首个与key相等元素结点，若查找不成功返回null
	    Node<T> q=null;
	    for (Node<T> p=this.head.next;  p!=null;  p=p.next){
	    if (key.equals(p.data)){                        //执行T类的equals(Object)方法，运行时多态
	    q=p;
        break;
	}
	}
	        return q;
	    }

	    

public Node<T> insertDifferent(T x){
 Node<T> front=this.head, p=front.next;  //front是p的前驱结点
	   while (p!=null && !p.data.equals(x)){               //顺序查找
	            front = p; 
	            p = p.next;
	        }
	        if (p!=null) {//查找成功，元素重复，不插入，返回p结点
	        System.out.println("x="+x+"，元素重复，未插入。");
	            return p;
	        }
	        return front.next = new Node<T>(x,null);           //尾插入值为x结点，返回插入结点
	    }
	    
	    public T remove(T key){ //删除首个与key相等元素结点，返回被删除元素；查找不成功返回null。O(n)散列表用
	    
	        Node<T> front=this.head, p=front.next;
	        while (p!=null && !key.equals(p.data)){             //顺序查找首次出现的与key相等元素
	            front = p;                                     //front指向p的前驱结点
	            p=p.next;
	        }
	        if (p!=null){                                       //若查找成功，删除front的后继（p结点）
	            front.next = p.next;                           //包括头删除、中间/尾删除
	            return p.data;
	        }
	        return null;
	    }
	}
3）编写一个单链表，运行程序，输出操作菜单
public class text {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		String qq[]= {"1","2","4","3","5"};
		SinglyList<String> list=new SinglyList<String>(qq);
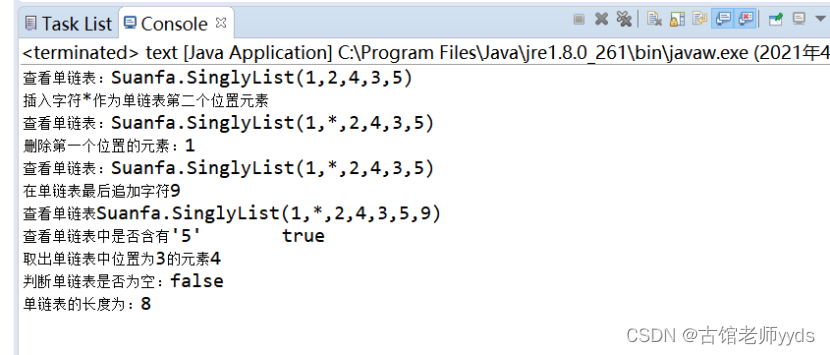
		System.out.println("查看单链表："+list.toString());
		System.out.println("插入字符"+list.insert(1,"*")+"作为单链表第二个位置元素");
		System.out.println("查看单链表："+list.toString());
		System.out.println("删除第一个位置的元素："+list.remove(0));
		System.out.println("查看单链表："+list.toString());
		System.out.println("在单链表最后追加字符"+list.insert("9"));
		System.out.println("查看单链表"+list.toString());
		System.out.println("查看单链表中是否含有'5'"+"\t"+list.contains("5"));
		System.out.println("取出单链表中位置为3的元素"+list.get(3));
		System.out.println("判断单链表是否为空："+list.isEmpty());
		System.out.println("单链表的长度为："+list.size());
		
	}

	}

结果运行截图

三、顺序表实现约瑟夫环

约瑟夫问题是个著名的问题：N个人围成一圈，第一个人从1开始报数，报M的将被杀掉，下一个人接着从1开始报。如此反复，最后剩下一个，求最后的胜利者。

要求：运行程序，输入约瑟夫环长度number、起始位置start、计数值distance，输出约瑟夫环执行过程。

（1）编写一个顺序表

public class SeqList <T> extends Object{
	protected Object[]element;
	protected int n;
	public SeqList(int length) {
		this.element=new Object[length];
		this.n=0;
	}
	public SeqList() {
		this(64);
	}
	public SeqList(T[] values) {
		this(values.length);
		for(int i=0;i<values.length;i++) 
	      this.element[i]=values[i];
	    this.n=element.length;
	}
	
	public boolean isEmpty() {
		return this.n==0;
	}
	
	public int size() {
		return this.n;
	}
	
	public T get(int i) {
		if(i>=0&&i<this.n)
			return(T)this.element[i];
		return null;
	}
	
	public void set(int i,T x) {
		if(x==null) throw new NullPointerException("x==null");
		if(i>=0&&i<this.n)
			this.element[i]=x;
		else throw new java.lang.IndexOutOfBoundsException(i+"");
	}
	public String toString() {
		String str=this.getClass().getName()+"(";
		if(this.n>0)
			str+=this.element[0].toString();
		for(int i=1;i<this.n;i++)
			str+=","+this.element[i].toString();
			return str+")";
	}

	public int insert(int i,T x) {
		if(x==null)throw new NullPointerException("x==null");
		if(i<0)i=0;
		if(i>this.n)i=this.n;
		Object[] source=this.element;
		if(this.n==element.length) {
			this.element=new Object[source.length*2];
			for(int j=0;j<i;j++)
				this.element[j]=source[j];
		}
		for(int j=this.n-1;j>=i;j--)
			this.element[j+1]=source[j];
		this.element[i]=x;
		this.n++;
		return i;
	}
	public int insert(T x) {
		return this.insert(this.n,x);
	}
	
  public T remove(int i) {
	if(this.n>0&&i>=0&&i<this.n) {
		T old=(T)this.element[i];
		for(int j=i;j<this.n-1;j++)
this.element[j]=this.element[j+1];
this.element[this.n-1]=null;
this.n--;
return old;
	}
	return null;
}
  public void clear() {
	  this.n=0;
  }
}

（2）约瑟夫环代码

public class Josephus {
 public Josephus(int number,int start,int distance) {
	    	System.out.print("Josephus("+number+","+start+","+distance+"),");
	    	SeqList<String>list=new SeqList<String>(number);
	    	for(int i=0;i<number;i++)
	    		list.insert((char)('A'+i)+"");
	    	System.out.println(list.toString());
	    	int i=start;
	    	while(list.size()>1) {
	    		i=(i+distance-1)%list.size();
	    		System.out.println("删除"+list.remove(i).toString());
	    		System.out.println(list.toString());
	    	}
	    	System.out.println("被赦免者是"+list.get(0).toString());
	    }
		public static void main(String[] args) {
			// TODO Auto-generated method stub
	         new Josephus(5,0,2);
		}
}

运行结果截图：

总结

单链表中的数据是以节点的形式存在的，每个节点有data域和next域组成，data域中存放的是节点的具体信息，next域中存放的是直接后继的存储位置。头节点：作为链表开始的标志。头节点的data域为空，即都取默认值；next域在只有头节点的空链表中也为空，在非空链表中存放的是下一个节点。在初始化时，是空链表，所以也是null。这里和创建节点类时的构造器不包含next域是一致的。

建议学习数据结构时书上的代码要多看，缺少的方法体在其他地方也都能找到，也可以在中国MOOC上查找类似课程，把不懂的再学一遍。