博客

入门算法学习，看的第一本是深入浅出的《算法图解》一书，本博客是对《算法图解》一书的学习笔记，将书中的分享的算法示例用Python3语言实现。

如果你也想要阅读这本书，百度云盘链接：

https://pan.baidu.com/s/1s967vfgEBd1vSrfwVI9Y3g

提取码：【be9k】

或者也可以留言你的邮箱，我将PDF共享给你~

二分查找

• 二分查找是一种算法，其输入是一个有序的元素列表（必须有序），如果要查找的元素包含在列表中，二分查找返回其位置；否则返回null。

二分查找工作原理

大家一定玩过‘猜数’这个游戏，就是我随便想一个1～100的数字。



你的目标是以最少的次数猜到这个数字。你每次猜测后，我会说小了、大了或对了。

假设你从1开始依次往上猜，猜测过程会是这样。



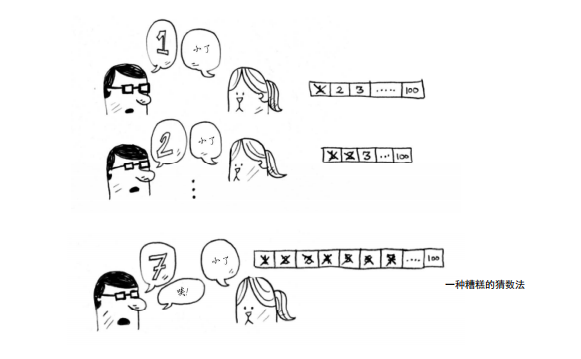
这是简单查找，更准确的说法是傻找。每次猜测都只能排除一个数字。如果我想的数字是99，


你得猜99次才能猜到！

最佳的查找方法是：







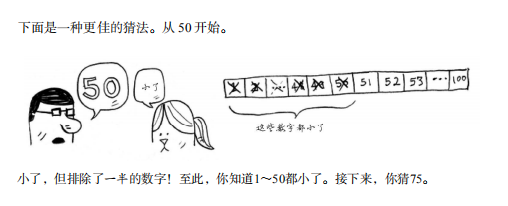
这就是二分查找，你学习了第一种算法！每次猜测排除的数字个数如下。




所以，

不管我心里想的是哪个数字，你在7次之内都能猜到

，因为每次

猜测都将排除很多数字！

仅当列表有序的时候，二分查找才管用!！

二分查找–案例

案例：函数binary_search接收一个”有序数组”和”一个元素”。

如果,指定的元素包含在数组中，这个函数将返回其位置。

def binary_search(list, num):                          
    low = 0                         # 最小索引
    high = len(list) - 1            # 最大索引

    while low <= high:
        mid = int((low + high) / 2)  # 向0取整，中间值的索引
        guess = list[mid]            # 猜中间值

        if guess == num:             # 找到了元素
            return ('got %d in index of %d') % (num, mid)

        if guess < num:              # 猜小了，增加最小索引
            low = mid + 1
        else:
            high = mid - 1           # 猜大了，缩小最大索引

    return None

my_list = [1,3,5,7,9]
find_num = 3
print(binary_search(my_list,find_num))
find_num1 = 4
print(binary_search(my_list,find_num1))

----------------------------
got 3 in index of 1
None      

运行时间

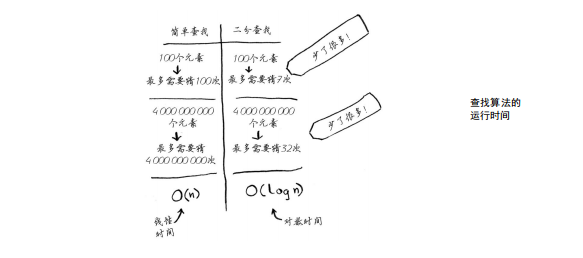
简单查找逐个地检查数字，如果列表包含100个数字，最多需要猜100次。如果列表包含40亿个数字，最

多需要猜40亿次。换言之，最多需要猜测的次数与列表长度相同，这被称为线性时间（linear time）。

二分查找则不同。如果列表包含100个元素，最多要猜7次；如果列表包含40亿个数字，最多

需猜32次。厉害吧？二分查找的运行时间为对数时间（或log时间）。