基本概念
-
随机变量、概率、概率分布和概率密度函数等的概念
-
条件概率、联合分布、全概率公式、贝叶斯法则
条件概率
两个随机变量
X,
Y
X,Y
X
,
Y
的
联合分布
由下式给出:
p(
x
,
y
)
=
p
(
X
=
x
,
Y
=
y
)
p(x, y) = p(X=x, Y=y)
p
(
x
,
y
)
=
p
(
X
=
x
,
Y
=
y
)
这个表达式描述了随机变量
X
X
X
取值为
x
x
x
并且
Y
Y
Y
取值
y
y
y
这一事件的概率,若
X
X
X
和
Y
Y
Y
相互独立
,则有以下结论
p
(
x
,
y
)
=
p
(
x
)
p
(
y
)
p(x, y) = p(x)p(y)
p
(
x
,
y
)
=
p
(
x
)
p
(
y
)
事实上,随机变量通常携带其他随机变量的信息,在已知
Y
=
y
Y = y
Y
=
y
的条件下,
X
=
x
X = x
X
=
x
的概率称为
条件概率
,表示为
p
(
x
∣
y
)
=
p
(
x
,
y
)
/
p
(
y
)
p(x|y) = {p(x, y)}/{p(y)}
p
(
x
∣
y
)
=
p
(
x
,
y
)
/
p
(
y
)
全概率公式:通过条件概率和概率测量公理,可以推出
全概率公式
如下
p
(
x
)
=
∑
y
p
(
x
∣
y
)
p
(
y
)
(
离
散
情
况
)
p
(
x
)
=
∫
p
(
x
∣
y
)
p
(
y
)
d
y
(
连
续
情
况
)
p(x) = \sum_{y}p(x|y)p(y) (离散情况)\\ p(x) = \int p(x|y)p(y){dy} (连续情况)
p
(
x
)
=
y
∑
p
(
x
∣
y
)
p
(
y
)
(
离
散
情
况
)
p
(
x
)
=
∫
p
(
x
∣
y
)
p
(
y
)
d
y
(
连
续
情
况
)
同样重要的还有
贝叶斯法则
:
p
(
x
∣
y
)
=
p
(
y
∣
x
)
p
(
x
)
p
(
y
)
=
p
(
y
∣
x
)
p
(
x
)
∑
x
′
p
(
y
∣
x
′
)
p
(
x
′
)
d
x
′
(
离
散
概
况
)
\begin{aligned} p(x|y)&= \frac{p(y|x)p(x)}{p(y)}\\&=\frac{p(y|x)p(x)}{\sum_{x’}{p(y|x’)p(x’)dx’}}(离散概况) \end{aligned}
p
(
x
∣
y
)
=
p
(
y
)
p
(
y
∣
x
)
p
(
x
)
=
∑
x
′
p
(
y
∣
x
′
)
p
(
x
′
)
d
x
′
p
(
y
∣
x
)
p
(
x
)
(
离
散
概
况
)
p
(
x
∣
y
)
=
p
(
y
∣
x
)
p
(
x
)
p
(
y
)
=
p
(
y
∣
x
)
p
(
x
)
∫
p
(
y
∣
x
′
)
p
(
x
′
)
(
连
续
情
况
)
\begin{aligned} p(x|y) &= \frac{p(y|x)p(x)}{p(y)}\\&=\frac{p(y|x)p(x)}{\int{p(y|x’)p(x’)}}(连续情况) \end{aligned}
p
(
x
∣
y
)
=
p
(
y
)
p
(
y
∣
x
)
p
(
x
)
=
∫
p
(
y
∣
x
′
)
p
(
x
′
)
p
(
y
∣
x
)
p
(
x
)
(
连
续
情
况
)
通常,由于
p
(
y
)
−
1
p(y)^-1
p
(
y
)
−
1
的值在同一个问题里面是不变的,所以可以使用
η
\eta
η
表示,称为贝叶斯法则中的归一化变量。
在贝叶斯法则中,如果
x
x
x
一个希望由
y
y
y
推测出来的数值,则概率
p
(
x
)
p(x)
p
(
x
)
称为先验概率分布。其中
y
y
y
称为数据
d
a
t
a
data
d
a
t
a
,也就是传感器测量值。
p
(
x
∣
y
)
p(x|y)
p
(
x
∣
y
)
称为
X
X
X
上的后验概率分布。通过贝叶斯法则,可以通过“逆”条件概率
p
(
y
∣
x
)
p(y|x)
p
(
y
∣
x
)
和先验概率
p
(
x
)
p(x)
p
(
x
)
一起起计算
p
(
x
∣
y
)
p(x|y)
p
(
x
∣
y
)
。所谓的逆条件概率,其实就是假设已知事件
x
x
x
发生的情况下,能够得到数据
y
y
y
的概率,它称为生成模型。
3.条件独立
以任意随机变量
Z
Z
Z
为条件的相互独立的两个变量
X
和
Y
X和Y
X
和
Y
,他们的概率满足
p
(
x
,
y
∣
z
)
=
p
(
x
∣
z
)
p
(
y
∣
z
)
p(x, y| z) = p(x|z)p(y|z)
p
(
x
,
y
∣
z
)
=
p
(
x
∣
z
)
p
(
y
∣
z
)
需要注意的是,条件独立并不意味为绝对独立,反之也不一定成立。
4.数学期望、协方差、熵
数学期望
即
均值
,可以由以下式求得
E
[
X
]
=
∑
x
x
p
(
x
)
(
离
散
)
E[X]=\sum_xxp(x)(离散)
E
[
X
]
=
x
∑
x
p
(
x
)
(
离
散
)
E
[
X
]
=
∫
x
p
(
x
)
d
x
(
连
续
)
E[X]=\int{xp(x)dx}(连续)
E
[
X
]
=
∫
x
p
(
x
)
d
x
(
连
续
)
数学期望具有
线性性质
协方差
可以由以下式子求得
C
o
v
[
X
]
=
E
[
X
−
X
[
x
]
2
]
=
E
[
X
2
]
−
E
[
X
]
2
Cov[X]=E[X-X[x]^2]=E[X^2] – E[X]^2
C
o
v
[
X
]
=
E
[
X
−
X
[
x
]
2
]
=
E
[
X
2
]
−
E
[
X
]
2
熵
,一个概率分布的熵可以按如下求得
H
p
(
x
)
=
E
[
−
l
o
g
2
p
(
x
)
]
H_p(x)=E[-log_2{p(x)}]
H
p
(
x
)
=
E
[
−
l
o
g
2
p
(
x
)
]
容易推导出
H
p
(
x
)
=
−
∑
x
p
(
x
)
l
o
g
2
p
(
x
)
H_p(x)=-\sum_x{p(x)log_2p(x)}
H
p
(
x
)
=
−
x
∑
p
(
x
)
l
o
g
2
p
(
x
)
H
p
(
x
)
=
−
∫
p
(
x
)
l
o
g
2
x
d
x
H_p(x)=-\int{p(x)log_2{x}dx}
H
p
(
x
)
=
−
∫
p
(
x
)
l
o
g
2
x
d
x
机器人环境交互
环境交互
-
环境传感器测量
-
控制动作改变世界状态
-
环境测量数据提供了环境的暂态信息,在
tt
t
时间里的测量数据表示为
zt
z_t
z
t
-
控制数据携带环境中关于状态改变的信息,控制数据用
ut
u_t
u
t
表示
状态和概率生成
状态用来表示环境特征,需要注意的是,
假设一个状态可以最好的预测未来,则称其为完整的。换句话说,完整性包裹过去的状态测量以及控制的信息,但是不包括其他可以更加精确的预测未来的附加信息
如果一个状态
x
x
x
是完整的,那么它是所有以前时刻发生的所有的状态的充分总结。用公式表示如下
p
(
x
t
∣
x
0
:
t
−
1
,
z
1
:
t
−
1
,
u
1
:
t
)
=
p
(
x
t
−
1
,
u
t
)
=
p
(
x
t
∣
x
t
−
1
,
u
t
)
p(x_t|x_{0:t-1},z_{1:t-1},u_{1:t}) = p(x_{t-1},u_t)=p(x_t|x_{t-1}, u_t)
p
(
x
t
∣
x
0
:
t
−
1
,
z
1
:
t
−
1
,
u
1
:
t
)
=
p
(
x
t
−
1
,
u
t
)
=
p
(
x
t
∣
x
t
−
1
,
u
t
)
同时,这个式子充分表达了
条件独立
的特性,这在以后会经常用到。
当状态
x
x
x
是完整的时,就有如下式子成立
p
(
z
t
∣
x
0
:
t
,
z
1
:
t
−
1
,
u
1
:
t
)
=
p
(
z
t
∣
x
t
)
p(z_t|x_{0:t},z_{1:t-1},u_{1:t})=p(z_t|x_t)
p
(
z
t
∣
x
0
:
t
,
z
1
:
t
−
1
,
u
1
:
t
)
=
p
(
z
t
∣
x
t
)
p
(
z
t
∣
x
t
)
p(z_t|x_t)
p
(
z
t
∣
x
t
)
称为
测量概率
,
p
(
x
t
∣
x
t
−
1
,
u
t
)
p(x_t|x_{t-1},u_t)
p
(
x
t
∣
x
t
−
1
,
u
t
)
称为
状态转移概率
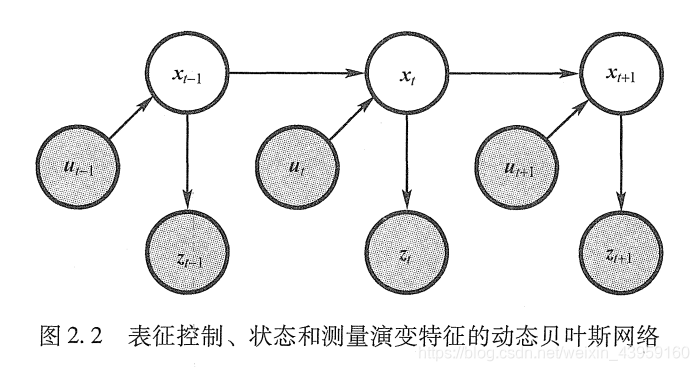
状态转移概率和测量概率一起描述机器人以及其环境组成的动态随即系统。图2.2所示的动态贝叶斯网络显示了由这些概率定义的状态和测量的演变。时刻
t
t
t
的状态依赖
t
−
1
t-1
t
−
1
时刻的状态和控制
u
t
u_t
u
t
,测量
z
t
z_t
z
t
随机的依赖时刻
t
t
t
的状态。这样的时间生成模型也称为隐形马尔可夫模型或动态贝叶斯网络。
置信度
概率机器人中另外一个重要的概念是
置信度分布
。置信度反映了机器人有关的环境状态的内部信息。概率机器人通过条件概率分布表示置信度,对于真实状态,置信度分布为每一种可能的假设分配一个概率(或者概率密度值)。置信度分布是以可获得的数据为条件的关于状态变量的后验概率。这里用
b
e
l
(
x
t
)
bel(x_t)
b
e
l
(
x
t
)
表示状态变量
x
t
x_t
x
t
的置信度,它是下式的缩写
b
e
l
(
x
t
)
=
p
(
x
t
∣
z
1
:
t
,
u
1
:
t
)
bel(x_t)=p(x_t|z_{1:t}, u_{1:t})
b
e
l
(
x
t
)
=
p
(
x
t
∣
z
1
:
t
,
u
1
:
t
)
这个后验是时刻
t
t
t
下状态
x
x
x
的概率分布,以
过去所有的测量
z
1
:
t
z_{1:t}
z
1
:
t
和过去所有的控制
u
1
:
t
u_{1:t}
u
1
:
t
为条件。
这个默认置信度是在综合了测量
z
t
z_t
z
t
之后得到的,有时,可以证明在刚刚执行完控制
u
t
u_t
u
t
之后,综合
z
t
z_t
z
t
之前计算后验是有效的。这个后验可以表示为
b
e
l
‾
(
x
t
)
=
p
(
x
t
∣
z
1
:
t
−
1
,
u
1
:
t
)
\overline{bel}(x_t)=p(x_t|z_{1:t-1}, u_{1:t})
b
e
l
(
x
t
)
=
p
(
x
t
∣
z
1
:
t
−
1
,
u
1
:
t
)
在概率滤波中,这个概率称为
预测
。它反映了一个事实:
b
e
l
‾
(
x
t
)
\overline{bel}(x_t)
b
e
l
(
x
t
)
是基于以前状态的后验,在综合测量
z
t
z_t
z
t
之前,预测了时刻
t
t
t
的状态,由
b
e
l
‾
(
x
t
)
\overline{bel}(x_t)
b
e
l
(
x
t
)
计算
b
e
l
(
x
t
)
bel(x_t)
b
e
l
(
x
t
)
称为修正或者
测量更新
。
贝叶斯滤波
算法描述
现在开始进入正题,大多数计算置信度的通用算法都是基于贝叶斯滤波算法的。算法描述如下
A
_
B
a
y
e
s
_
f
i
l
t
e
r
(
b
e
l
(
x
t
)
,
u
t
,
z
t
)
:
f
o
r
a
l
l
x
t
d
o
b
e
l
‾
(
x
t
)
=
∫
p
(
x
t
∣
u
t
,
x
t
−
1
)
p
(
x
t
−
1
)
d
x
t
−
1
b
e
l
(
x
t
)
=
η
p
(
z
t
∣
x
t
)
b
e
l
‾
(
x
t
)
e
n
d
f
o
r
r
e
t
u
r
n
b
e
l
(
x
t
)
\begin{aligned} A\_B&ayes\_filter(bel(x_t), u_t, z_t):\\ &for\ all\ x_t\ do\\ &\quad\ \overline{bel}(x_t) = \int{p(x_t|u_t, x_{t-1})p(x_{t-1})}dx_{t-1}\\ &\quad\ bel(x_t)= \eta p(z_t|x_t)\overline{bel}(x_t)\\ &end \ for\\ &return\ bel(x_t) \end{aligned}
A
_
B
a
y
e
s
_
f
i
l
t
e
r
(
b
e
l
(
x
t
)
,
u
t
,
z
t
)
:
f
o
r
a
l
l
x
t
d
o
b
e
l
(
x
t
)
=
∫
p
(
x
t
∣
u
t
,
x
t
−
1
)
p
(
x
t
−
1
)
d
x
t
−
1
b
e
l
(
x
t
)
=
η
p
(
z
t
∣
x
t
)
b
e
l
(
x
t
)
e
n
d
f
o
r
r
e
t
u
r
n
b
e
l
(
x
t
)
-
贝叶斯滤波算法的第一步叫做控制更新,即上述描述的第3行,通过基于状态
xt
−
1
x_{t-1}
x
t
−
1
的置信度和控制
ut
u_t
u
t
来计算
xt
x_t
x
t
的置信度,这种跟新称为
控制更新
或者
预测
-
贝叶斯滤波算法的第二个步骤叫做测量更新,位于上述描述的第4行。书上说的有点迷糊,其实就是一个贝叶斯公式。根据上一次状态和这一次控制,得到新的预测为先验概率,配合生成模型计算后验概率
be
l
(
x
t
)
bel(x_t)
b
e
l
(
x
t
)
. -
通过上述的分析,不难发现,要使用这样一个算法,我们需要知道一个初始状态
be
l
(
x
0
)
bel(x_0)
b
e
l
(
x
0
)
作为边界条件。如果知道
x0
x_0
x
0
的确切的值,应当使用一个点式群体分布进行初始化。若不知道,或者可以完全忽略
x0
x_0
x
0
的初始值,则应使用一个
x0
x_0
x
0
的邻域上的均匀分布(或者狄氏分布的相关分布)来进行初始化。
贝叶斯滤波的数学推导
机器人判断门的开闭的示例就不赘述了,接下来看贝叶斯滤波的数学推导。
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(x_t|z_{1:t},…
由第 1 行到第 2 行的变化是由于
x
t
x_t
x
t
是一个完整的状态变量,且跟其他两个条件条件独立,所以可以忽略其他条件。
第 2 行到第 3 行是一个简单的全概率公式。
最后,要注意,对于任意所选的控制,可以从条件变量集
p
(
x
t
−
1
∣
z
1
:
t
−
1
,
u
t
)
p(x_{t-1}|z_{1 : t-1},u_t)
p
(
x
t
−
1
∣
z
1
:
t
−
1
,
u
t
)
中安全地将控制
u
t
u_t
u
t
省略,因此,上述方程可以写作
p
(
x
t
∣
z
1
:
t
,
u
1
:
t
)
=
η
p
(
z
t
∣
x
t
)
∫
p
(
x
t
∣
x
t
−
1
)
p
(
x
t
−
1
∣
z
1
:
t
−
1
,
u
1
:
t
−
1
)
d
x
t
−
1
p(x_t|z_{1:t},u{1:t})=\eta p(z_t|x_t)\int p(x_t|x_{t-1})p(x_{t-1}|z_{1:t-1},u_{1:t-1})dx_{t-1}
p
(
x
t
∣
z
1
:
t
,
u
1
:
t
)
=
η
p
(
z
t
∣
x
t
)
∫
p
(
x
t
∣
x
t
−
1
)
p
(
x
t
−
1
∣
z
1
:
t
−
1
,
u
1
:
t
−
1
)
d
x
t
−
1
这个递归更新方程在贝叶斯滤波算法的第三行得到了实现。
总之,贝叶斯滤波算法以到时间
t
t
t
的测量和控制数据为条件来计算状态
x
t
x_t
x
t
的后验。推导假设世界是马尔可夫的,也就是状态是完整的。
可以看到,该算法的任意具体实现都需要三个条件概率分布,分别是:
初始置信度分布
p
(
x
0
)
p(x_0)
p
(
x
0
)
、测量概率分布
p
(
z
t
∣
x
t
)
p(z_t|x_t)
p
(
z
t
∣
x
t
)
和状态转移概率
p
(
x
t
∣
u
t
,
x
t
−
1
)
p(x_t|u_t,x_{t-1})
p
(
x
t
∣
u
t
,
x
t
−
1
)
。
PS:这一章内容其实不算少,但是除了前面的基础知识,核心的算法也就几页,看明白了之后,其实也就那么回事,但是在这之前,会觉得很难很烦。这里建议,首先要克服这种负面情绪,其实原理很简单,静下心来慢慢看。另外很重要的一点就是,书后面的习题真的很好,认真做一做,非常非常非常有帮助。但是刚开始做其实会比较迷惑,一个是不知道自己做的对不对,另一个是这对于低年级本科生来说,还是一个比较陌生的模式,难免会有一点不适应。对于习题答案这个问题,网上很少有完整的一套答案,即便有也只是零零散散几道题,而且很可能你哪道题不会了,恰好就找不到那一道题,这里推荐一个大佬分享的这本书完整的
答案