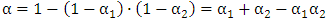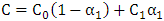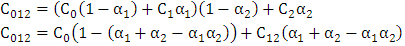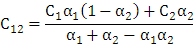叠加算法原理:
通过一些简单的实验外加一些逻辑推理,可以成功的找到 Alpha 混合的方法。这里为了计算上的方便,全部颜色分量值的取值范围都是 0 ~ 1。
首先是透明度值的计算。颜色在本质上是光的产物,假设把透明度理解为玻璃的透光性,则一切就变得很easy。比如一个 alpha = 0.2 的颜色,就能够将其想像为透光率为 80% 的彩色玻璃。我们透过这块玻璃看去,因为 80% 的光都透过了,因此留下来的颜色仅仅剩 20%,即所谓 0.2 的 alpha。如今我们来做一个混合:将 alpha 为 0.2 和 0.6 的颜色进行叠加。这时,我们有了两块玻璃,一块透光率为 80%,还有一块为 40%。一道光束穿过,经过 80% 透光率的玻璃时,光线强度剩下 80%,再经过 40% 透光率的玻璃时,光线进一步被削弱,仅仅剩下 80% * 40% = 32%。这意味着有 32% 的透明性,即 alpha = 0.68。
总结上面的算法,我们能够得出:
下一步,是依据已有的透明度来计算每一个通道的颜色分量。这其有用数学推导的方法更easy一些。我们已经知道,在背景色上怎样叠加半透明色,其 RGB 颜色分量的计算方法为:
那么,我们能够通过在背景色上叠加两个半透明颜色的不同方法来进行公式推导。第一种叠加方式:先在背景色上叠上第一个半透明颜色,再在叠好的结果上叠上第二个半透明颜色;另外一种方式则是先将两个半透明颜色叠好,再与背景色混合。即:
这两种混合方式的结果应当是全然一致的,则有
整理,得
这即是 RGB 模式下的 Alpha 混合公式。对于 CMYK 等其它模式,也能够用类似的方式推导。
代码实现:
class CColor
{
public:
CColor(unsigned char a, unsigned char r, unsigned char g, unsigned char b)
{
m_alph = a;
m_red = r;
m_green = g;
m_blue = b;
}
// others...
private:
unsigned char m_alph;
unsigned char m_red;
unsigned char m_green;
unsigned char m_blue;
}
float crCalculateBlend(float a1, float a2, float c1, float c2)
{
return (c1 * a1 * (1.0 - a2) + c2 * a2) / (a1 + a2 - a1 * a2);
}
const CColor crColorBlend(const CColor& cor1, const CColor& cor2)
{
float fAlp1 = cor1.GetAlpha() / 255.0;
float fAlp2 = cor2.GetAlpha() / 255.0;
float fAlpBlend = fAlp1 + fAlp2 - fAlp1 * fAlp2;
float fRed1 = cor1.GetRed() / 255.0;
float fRed2 = cor2.GetRed() / 255.0;
float fRedBlend = crCalculateBlend(fAlp1, fAlp2, fRed1, fRed2);
float fGreen1 = cor1.GetGreen() / 255.0;
float fGreen2 = cor2.GetGreen() / 255.0;
float fGreenBlend = crCalculateBlend(fAlp1, fAlp2, fGreen1, fGreen2);
float fBlue1 = cor1.GetBlue() / 255.0;
float fBlue2 = cor2.GetBlue() / 255.0;
float fBlueBlend = crCalculateBlend(fAlp1, fAlp2, fBlue1, fBlue2);
return CColor(fAlpBlend * 255, fRedBlend * 255, fGreenBlend * 255, fBlueBlend * 255);
}