注:为了简化代码,提高语义,本文将HashMap很多核心代码抽出并根据代码含义为代码片段取名,完全是为了方便读者理解。
哈希函数的作用与本质
HashMap
用来存储具有映射关系的数据对
{key, value}
,在内部通过构造复合数据结构来封装数据对,即
//伪代码,非源码
class Pair<K, V> {
public K key;
public V value;
}
假设用来存储数据对的哈希数表为
table
,数据对
Pair
的存储位置通过计算
key
得到,
key => index
,则
Pair
将存储在
table[index]
处。
哈希函数就是用来计算哈希索引的工具。
fun(key,table) = index, 0 <= index < table.length
入参
key
为整数,若
key
不为整数,则需要先将
key
转化为整数再参与计算。在
Java
中,每个对象都有一个
public int hashCode();
方法,起的就是这样的转化作用。
哈希函数设计
构造哈希函数最常见的策略是取余法,即
index = int_key % table.length
。
HashMap
也是采用取余法构造哈希函数,并强制哈希表的容量
table.length
为2的整数次幂,即2^n,这样便可采用位运算计算余数以提高运算效率:
(table.length - 1) & key.hashCode()
。
因为当
table.length = 2^n
时,其二进制形式只有第(n + 1)位为1,其余皆为0。任何一个整数对
table.length
求余,实际上就是取这个整数的低n位的值。
例如
table.length = 16 = 2^4
,直接通过模运算将得到
18 % 16 = 2
。

而
table.length - 1 = 2^n -1
,其二进制形式低n位均为1,其余比特位皆为0。
以
table.length = 16 = 2 ^ 4
为例,
table.length - 1 = 15
,即
0000 0000 0000 0000 0000 0000 0000 1111
,低4位均为1,其余比特位皆为0
table.length - 1
恰好是对任意一个整数低n位的遮罩, 当用这个遮罩与任意一个整数进行位与操作时,恰好得到这个整数对table.length求余的余数。
那么18 & (16 -1) = 18 % 16 = 2,

哈希表初始容量的校正
创建
HashMap
时,允许指定哈希表的初始容量,即
table.length
。
HashMap
没有强制要求使用者传入的初始容量为2的整数次幂,而是在内部自动转化。若使用者传入的初始容量为
capacity
,那么转化后的哈希表容量为大于等于
capacity
的最小的一个2的整数次幂。如,9~15都会转为为
16 = 2^4
,17~31都会转成
2^5 = 32
,以此类推。
从二进制的角度看,使用者传入的初始容量为
capacity
(先不考虑
capacity
恰好是2的整数次幂的情况),如果它比特值为1的最高位处在第k位,那么转化后的值就是2^k。
以
129 = 2 ^7 + 1
为例,
比特值为1的最高位处在第8位,那么转化后的值便是2^8 = 256。

HashMap
采用的策略是,如果初始容量
capacity
的比特值为1的最高位处在第k位,那么将低(k – 1)位全部置为1,再把结果值 + 1,恰好得到转换后的目标容量。以
129 = 2 ^7 + 1
为例,比特值为1的最高位处在第8位,那么将低7位全部置为1得到255,255再加1等于256。

具体计算方法上,将
capacity
不断进行无符号右移再与原值进行位或操作,我们还是通过
capacity = 129
,
k = 8
来一步步说明。
第一步,将129无符号右移一位,得到结果64,结果的第k-1位必定为1。

然后将129与64做位或操作得到结果193,由于位或操作中,两个比特为只要有一个为1,那么结果必为1,如此,确保了最终结果第k – 1位变为1。

第二步,经过第一步,第k位,k – 1位都为1,所以我们可以把193无符号右移2位,得到结果48,结果的第k-2位及第k-3位必定为1。

然后将193与48做位或操作,得到结果241,最终结果第k位到第(k – 3)位,总共四位都变为1。

第三步,经过前面的操作,得到的结果241的第k位到(k-3)位,总共四位均变为1,所以将241无符号右移4位,得到结果15,其低4位均为1。

再将241与15进行位或操作,得到结果255,至此目标结果的低8位全部置为1。

因为用户传入的初始容量
capacity
,其比特值为1的最高位可能是第31位,所以为了囊括所有的可能,会继续无符号右移,直至移够31位,每次移动的位数恰好是上一次的2倍。
对于上面的例子,接下来要无符号右移8位。将255 无符号右移8位得到0。

将255与0进行位或,结果不变还是255。

接下来,位移16位,结果为0,再与255位或,结果还是255。至此已经总共无符号右移了
(1 + 2 + 4 + 8 + 16) = 31
位,位移结束。
最后,
255 + 1 = 256
。

按照上面的算法,哈希表初始容量的校正代码如下:
int adjustCapacity(int cap) {
int n = cap;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return n
}
我们还有遗留的一个问题没有讨论,假如使用者传入的初始容量
capacity
本来就是2的整数次幂,如
capacity = 128 = 2^(k - 1)
,
k = 8
,那么将低
(k - 1) = 7
位全部置为1,将得到255。这是完全没必要的,因为我们可以直接采用128。

那么,如果想把这样的
capacity
也统一到我们的计算公式里,我们只需要在开始位移前,将初始容量减1,然后再开始位移。比如
capacity = 128
,
c - 1 = 127
,127的二进制表示法中,比特值为1的最高位处在第7位,将其低6位全部置为1,结果还是127,然后加1得到目标结果128。

对于初始容量
capacity
不是2的整数次幂的情况,将
capacity - 1
再通过
adjustCapacity
计算,结果跟直接通过
capacity
计算的结果一致。
最后再考虑下边界值问题。
当
capacity = 0
,直接取
1 = 2^0
,
在java中,一个int值能表示的最大的2的整数次幂是2^(k -1),k = 31,即2^30,所以当
capacity
的二进制形式中,比特值为1最
高位处在第31位时,那么位移结束后目标结果将是
2^32 - 1
,
即除了符号位全是1,此时再加1将产生溢出,所以直接取2^30。
最终的adjustCapacity如下:
int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
哈希表容量为2的整数次幂的缺陷及解决办法
当哈希表容量为2的整数次幂时,即
capacity = 2^m
,那么任何整数对其求余,等同于取该整数二进制表示形式的低m位的值。
比如
capacity = 16 = 2^4
。
key = 65538
时,
65538 & (16 -1) = 2
,也就是取65538的低4位的值。

key = 2
时,
2 & (16 -1) = 2
,取低4位的值还是2。

通过这个例子我们可以发现,当哈希表容量为2的整数次幂时,即
capacity = 2^m
,只要key的低m位的值相同,他们通过求余法计算的哈希索引就相等,即产生了哈希冲突。
为了降低产生哈希冲突的概率,我们需要利用剩余比特位的值。
首先将key无符号右移16位,得到一个结果,这个结果的高16位为0,低16位为原先的高16的值,以65538为例,

接着将位移后的结果与key的原值进行位异或操作,由于比特值0与任何比特值位异或得到都是后者本身,比热值1与任何比热值位异或得到都是后者取反后的值。那么原高16位中值为1的比特位就会改变低16位中对应位置的比特值。

再将这个结果作为新的key代入哈希函数计算,
65539 & (16 - 1) = 3
。

当
key = 2
,2无符号右移16位,得到0。

2跟0进行位异或还是2。

最后将2作为最终结果代入哈希函数计算,得到结果0。
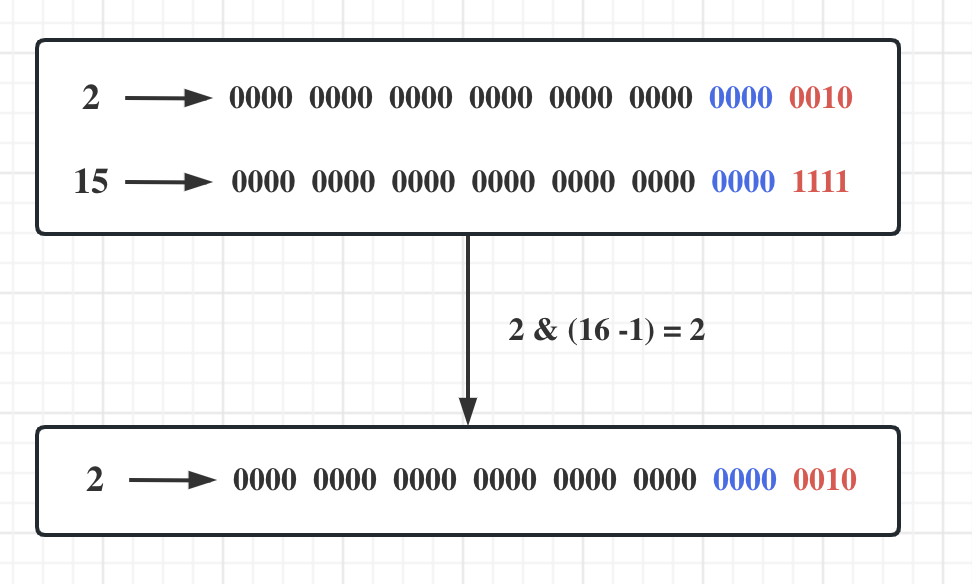
通过这样的操作,虽然2和65538的低4位相同,但得出的哈希索引却不同,从而降低了哈希碰撞的概率。
最终的哈希函数变为:
//先对key进行转化,降低哈希碰撞的概率
int transformKey(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
int hash(int key){
//table.length为2的整数次幂,所以可通过位运算取代模运算,提高运算效率
return (table.length - 1) & key;
}