陈宝林《最优化理论与算法》超详细学习笔记 (一)————第十章 使用导数的最优化方法(最速下降法、牛顿法、阻尼牛顿法)
写在前面
最优化理论与算法是一个重要的数学分支,顾名思义,这是一门研究在众多解决方案中确定什么样的方案是最优方案以及如何找到最优方案的学科。现如今,随着计算机科学的飞速发展,最优化理论与算法也迅速发展起来,成为了求解的有力工具,发挥着越来越来的作用。于是,为了给机器学习提供有力的理论支撑,现以清华大学出版社出版、
陈宝林编著的《最优化理论与算法》
为教材,开始学习这门课。学习的顺序根据同时在学习的《机器学习》的需要有所调整。
第十章 使用导数的最优化方法
在解决无约束问题的算法中,大致可以分为两类:一类要利用目标函数的导数,另一类只用到目标函数,称为
直接方法
。本章学习的是前一类
使用导数的最优化方法
中的
最速下降法
、
牛顿法
、
阻尼牛顿法
。
最速下降法
为了求解目标函数的最小值时,从点
x
0
x_0
x
0
出发,我们可以自然地想到沿着函数值在
x
0
x_0
x
0
点下降最快的方向有利于尽快找到极小值点,于是数学家们根据这一思想提出了
最速下降法
。
对于刚刚说的“下降最快方向”,根据高等数学知识,一般地(指欧式度量意义)在
负梯度方向
下为
最速下降方向
,即:
d
=
−
∇
f
(
x
)
\textbf{d}=-∇f(\textbf{x})
d
=
−
∇
f
(
x
)
回到刚开始的设想,现在我们找到了下降最快的方向来寻找最小值点,显然我们要经过多次寻找来逐渐逼近极小值点,所以要从
x
0
\textbf{x}_0
x
0
沿最速下降方向搜索多远找到下一个点
x
1
\textbf{x}_1
x
1
呢?
我们不妨假设变量?,称为
一维搜索的步长
:
x
1
=
x
0
+
λ
d
0
\textbf{x}_1=\textbf{x}_0+\lambda \textbf{d}_0
x
1
=
x
0
+
λ
d
0
也就是说
x
1
x_1
x
1
是关于?的变量,那么
f
(
x
1
)
f(\textbf{x}_1)
f
(
x
1
)
也是关于?的变量,由于求目标函数的最小值,所以我们在此令
f
(
x
1
)
f(\textbf{x}_1)
f
(
x
1
)
取最小值,求此时的?,即:
λ
0
=
argmax
λ
f
(
x
1
)
\mathop{\lambda _0=\underset{\lambda}{\operatorname{argmax}} f(x_1)}
λ
0
=
λ
a
r
g
m
a
x
f
(
x
1
)
于是,我们可以得到,以此类推:
x
2
=
x
1
+
λ
1
d
1
\textbf{x}_2=\textbf{x}_1+\lambda _1 \textbf{d}_1
x
2
=
x
1
+
λ
1
d
1
…
…
……
…
…
当最速下降方向的模足够小时,我们认为已经足够逼近最小值点,即:
∥
d
k
∥
<
ϵ
\| \textbf{d}_k\|<\epsilon
∥
d
k
∥
<
ϵ
停止迭代,最小值点为
x
k
\textbf{x}_k
x
k
。
所以,最速下降算法步骤为:
-
给定初始点
x0
\textbf{x}_0
x
0
,允许误差
ϵ>
0
\epsilon>0
ϵ
>
0
,置
k=
0
k=0
k
=
0
; -
计算搜索方向
dk
=
−
∇
f
(
x
k
)
\textbf{d}_k=-∇f(\textbf{x}_k)
d
k
=
−
∇
f
(
x
k
)
; -
如果
∥d
k
∥
<
ϵ
\| \textbf{d}_k\|<\epsilon
∥
d
k
∥
<
ϵ
,则停止运算;否则,从
xk
\textbf{x}_k
x
k
出发,沿
dk
\textbf{d}_k
d
k
进行一维搜索
xk
+
1
=
x
k
+
λ
k
d
k
\textbf{x}_{k+1}=\textbf{x}_k+\lambda _k \textbf{d}_k
x
k
+
1
=
x
k
+
λ
k
d
k
,其中
λk
=
argmax
λ
f
(
x
k
)
\mathop{\lambda _k=\underset{\lambda}{\operatorname{argmax}} f(x_k)}
λ
k
=
λ
a
r
g
m
a
x
f
(
x
k
)
-
得到
xk
+
1
\textbf{x}_{k+1}
x
k
+
1
,置
k=
k
+
1
k=k+1
k
=
k
+
1
;转到步骤2;
牛顿法
第二种方法是牛顿法,我们先来看下图。
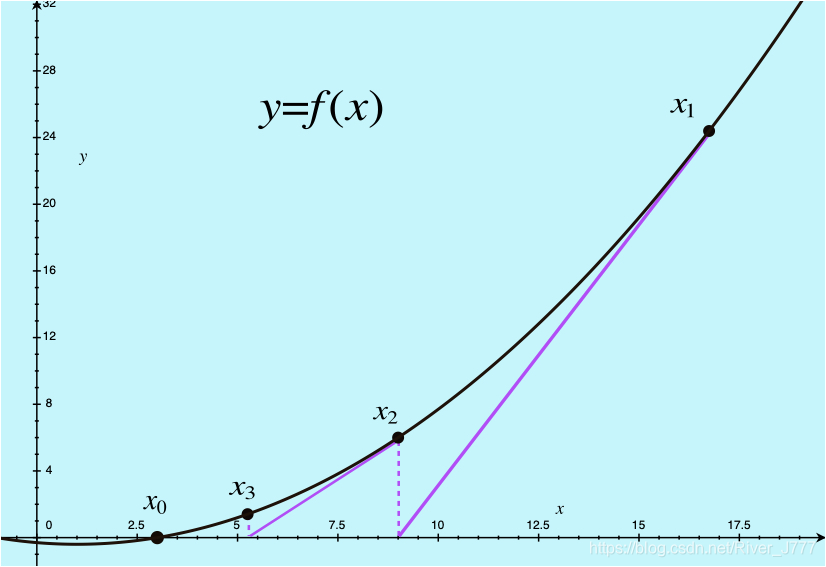
对于函数
y
=
f
(
x
)
y=f(x)
y
=
f
(
x
)
,我们希望找到它的其中一个零点
x
0
x_0
x
0
。
于是我们从任意一点
x
1
x_1
x
1
出发,
从点
x
1
x_1
x
1
作曲线的切线,切线与
y
y
y
轴交于
x
=
x
2
x=x_2
x
=
x
2
;
再从点
x
2
x_2
x
2
作曲线的切线,切线与轴交于
x
=
x
3
x=x_3
x
=
x
3
;
…
…
…
…
…………
…
…
…
…
可以看到
x
1
,
x
2
,
x
3
,
.
.
.
,
x
n
x_1,x_2,x_3,…,x_n
x
1
,
x
2
,
x
3
,
.
.
.
,
x
n
逐渐向
x
0
x_0
x
0
逼近。
我们根据切线的表达式
y
−
f
(
x
k
)
=
f
′
(
x
k
)
(
x
−
x
k
)
y-f(x_k)=f'(x_k)(x-x_k)
y
−
f
(
x
k
)
=
f
′
(
x
k
)
(
x
−
x
k
)
令
y
=
0
y=0
y
=
0
,可以解得:
x
k
+
1
=
x
k
−
f
(
x
k
)
f
′
(
x
k
)
x_{k+1}= x_k- {
{f(x_k)}\over {f'(x_k)}}
x
k
+
1
=
x
k
−
f
′
(
x
k
)
f
(
x
k
)
这就是牛顿法的图形解释,下面是数学推导。
数学推导:
对于函数
f
(
x
)
f(x)
f
(
x
)
,假设
x
k
x_k
x
k
是
f
(
x
)
f(x)
f
(
x
)
极小值点的一个估计,我们将
f
(
x
)
f(x)
f
(
x
)
在
x
=
x
k
x=x_k
x
=
x
k
处展开,得到:
f
(
x
)
≈
ϕ
(
x
)
=
f
(
x
k
)
+
f
′
(
x
k
)
(
x
−
x
k
)
+
1
2
f
′
′
(
x
k
)
(
x
−
x
k
)
2
f(x)\approx \phi(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2}f”(x_k)(x-x_k)^2
f
(
x
)
≈
ϕ
(
x
)
=
f
(
x
k
)
+
f
′
(
x
k
)
(
x
−
x
k
)
+
2
1
f
′
′
(
x
k
)
(
x
−
x
k
)
2
为求
ϕ
(
x
)
\phi(x)
ϕ
(
x
)
的平稳点,便要使一阶导数等于零,令:
ϕ
′
(
x
)
=
0
\phi'(x)=0
ϕ
′
(
x
)
=
0
即:
ϕ
′
(
x
)
=
f
′
(
x
k
)
+
f
′
′
(
x
k
)
(
x
−
x
k
)
=
0
\phi'(x)=f'(x_k)+f”(x_k)(x-x_k)=0
ϕ
′
(
x
)
=
f
′
(
x
k
)
+
f
′
′
(
x
k
)
(
x
−
x
k
)
=
0
整理出
x
x
x
的表达式,为:
x
=
x
k
−
f
′
(
x
k
)
f
′
′
(
x
k
)
x= x_k- {
{f'(x_k)}\over {f”(x_k)}}
x
=
x
k
−
f
′
′
(
x
k
)
f
′
(
x
k
)
我们将上式作为的迭代公式,即:
x
k
+
1
=
x
k
−
f
′
(
x
k
)
f
′
′
(
x
k
)
x_{k+1}= x_k- {
{f'(x_k)}\over {f”(x_k)}}
x
k
+
1
=
x
k
−
f
′
′
(
x
k
)
f
′
(
x
k
)
这里的
f
′
(
x
)
f'(x)
f
′
(
x
)
其实就相当于图形中的
f
(
x
)
f(x)
f
(
x
)
即需要找到零点的函数,且表达式与切线方程推导出的是相同的。
我们将其推广到高维函数,得:
x
k
+
1
=
x
k
−
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
\textbf{x}_{k+1}= \textbf{\textbf{x}}_k- {\nabla ^2f(\textbf{x}_k)}^{-1}{\nabla f(\textbf{x}_k)}
x
k
+
1
=
x
k
−
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
并且可以证明牛顿法是收敛的。(略)
阻尼牛顿法
阻尼牛顿法与牛顿法的区别在
x
k
+
1
=
x
k
−
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
\textbf{x}_{k+1}= \textbf{\textbf{x}}_k- {\nabla ^2f(\textbf{x}_k)}^{-1}{\nabla f(\textbf{x}_k)}
x
k
+
1
=
x
k
−
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
的迭代公式中,仿照最速下降法的方法,加入参数
λ
\lambda
λ
作为一维搜索步长,即:
x
k
+
1
=
x
k
−
λ
k
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
\textbf{x}_{k+1}= \textbf{\textbf{x}}_k- \lambda_k{\nabla ^2f(\textbf{x}_k)}^{-1}{\nabla f(\textbf{x}_k)}
x
k
+
1
=
x
k
−
λ
k
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
这样看来拟牛顿法与最速下降法的区别就只是将最速下降下降方向-∇?(?
k
_k
k
)替换成牛顿方向
−
λ
k
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
– \lambda_k{\nabla ^2f(\textbf{x}_k)}^{-1}{\nabla f(\textbf{x}_k)}
−
λ
k
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
。
类似最速下降法,我们得到阻尼牛顿法的算法步骤:
-
给定初始点
x0
\textbf{x}_0
x
0
,允许误差
ϵ>
0
\epsilon>0
ϵ
>
0
,置
k=
0
k=0
k
=
0
; -
计算搜索方向
dk
=
−
λ
k
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
\textbf{d}_k=-\lambda_k{\nabla ^2f(\textbf{x}_k)}^{-1}{\nabla f(\textbf{x}_k)}
d
k
=
−
λ
k
∇
2
f
(
x
k
)
−
1
∇
f
(
x
k
)
; -
如果
∥d
k
∥
<
ϵ
\| \textbf{d}_k\|<\epsilon
∥
d
k
∥
<
ϵ
,则停止运算;否则,从
xk
\textbf{x}_k
x
k
出发,沿
dk
\textbf{d}_k
d
k
进行一维搜索
xk
+
1
=
x
k
+
λ
k
d
k
\textbf{x}_{k+1}=\textbf{x}_k+\lambda _k \textbf{d}_k
x
k
+
1
=
x
k
+
λ
k
d
k
,其中
λk
=
argmax
λ
f
(
x
k
)
\mathop{\lambda _k=\underset{\lambda}{\operatorname{argmax}} f(x_k)}
λ
k
=
λ
a
r
g
m
a
x
f
(
x
k
)
-
得到
xk
+
1
\textbf{x}_{k+1}
x
k
+
1
,置
k=
k
+
1
k=k+1
k
=
k
+
1
;转到步骤2;
另外一篇对数几率回归的博客中,使用 python实现了牛顿法以计算目标函数最小值
周志华《机器学习》西瓜书 小白Python学习笔记(二)————第三章 线性模型 (对数几率回归)附课后题3.3详解
阻尼牛顿法相比牛顿法的优势在于,阻尼牛顿法可以保证每次迭代后函数值下降或不变。可以证明阻尼牛顿法在适当的条件下具有全局收敛性,且为2级收敛。
注:教材中一般表示为
x
(
k
)
\textbf{x}^{(k)}
x
(
k
)
,本文表示为
x
k
\textbf{x}_k
x
k
.