目录
LASSO
此算法通过构造一个一阶惩罚函数获得一个精炼的模型,
通过最终确定一些指标(变量)的系数为0
(
岭回归估计系数等于0的概率微乎其微
,造成筛选变量困难),解释力很强。LASSO算法擅长处理具有多重共线性的数据,与岭回归一样是有偏估计。
岭回归代价函数:
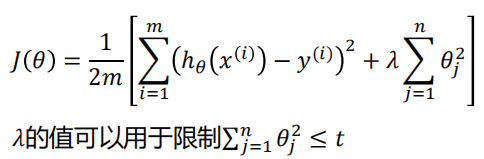
LASSO代价函数:
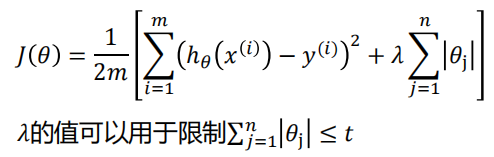
LASSO回归和岭回归最大的区别就是LASSO回归更容易使一些对回归没有贡献的系数等于0,直接可以去掉为0的系数,模型的输出不会改变。但是岭回归只能让系数趋于0,如果去掉这些系数,会对模型的效果有所损伤。
sklearn—-LASSO回归代码实现
- 需要用到的库导入
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
%matplotlib inline- 将数据导入,进行数据处理
data = np.genfromtxt(r'longley.csv',delimiter=',')
print(data)
x_data =data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)- 创建模型
model = linear_model.LassoCV()
model.fit(x_data,y_data)
print(model.alpha_) #lasso 系数
print(model.coef_) #相关的系数 从打印的结果可以看出 lasso可以通过最终确定一些指标为0,这样可以减小计算量
创建模型结束后,打印出弹性系数以及其他相关系数

我们可以看到相关系数的后三个都是0,这也就是对回归没有贡献的系数,我们可以去掉。
- 做预测
#做预测 和y_data的值比较
model.predict(x_data[-2,np.newaxis])
上边的代码表示我们对x_data的倒数第2行数据进行预测,它的真实值对应的是y_data的倒数第二个数据,由上边的数值图我们可以看到真实值为115.7,我们的预测结果显示
![]()
数值很接近,模型训练成功!
弹性网
弹性网是一种使用L1和L2先验作为正则化矩阵的线性回归模型,是综合LASSO回归和岭回归的一种回归算法。弹性网将代价函数中的后半部分处理成了以下的形式:
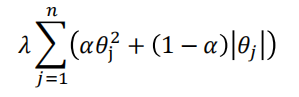
sklearn—-弹性网回归代码实现
- 需要用到的库导入
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
%matplotlib inline- 将数据导入,进行数据处理
data = np.genfromtxt(r'longley.csv',delimiter=',')
print(data)
x_data =data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)- 创建模型
model = linear_model.ElasticNetCV()
model.fit(x_data,y_data)
print(model.alpha_) #弹性往系数
print(model.coef_) #相关系数 - 做预测
#做预测
model.predict(x_data[-2,np.newaxis])
上边的代码表示我们对x_data的倒数第2行数据进行预测,它的真实值对应的是y_data的倒数第二个数据,由上边的数值图我们可以看到真实值为115.7,我们的预测结果显示
![]()
数值很接近,模型训练成功!