一、背包九讲总述
关于动态规划问题,最典型的就是背包九讲,先理解背包九讲后再总结关于动态规划的问题。
1、01背包问题
2、完全背包问题
3、多重背包问题
4、混合背包问题
5、二维费用的背包问题
6、分组背包问题
7、背包问题求方案数
8、求背包问题的方案
9、有依赖的背包问题
往前三篇博客分别介绍了01背包、完全背包和多重背包,有需要的可以看一下。
二、混合背包问题
混合背包问题就是混合01背包、完全背包和多重背包,可供选择的物体i可能有一个、或者无数个、或者有限个。
所以,就不要考虑这么多了,直接分这三种情况考虑就行!!
#include<iostream>
#include<algorithm>
using namespace std;
int C, n;
int w[35], v[35], k[35], f[205] = { 0 };//h,much,num,a
int main()
{
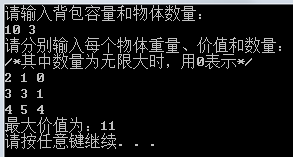
cout << "请输入背包容量和物体数量:" << endl;
cin >> C >> n;
cout << "请分别输入每个物体重量、价值和数量:" << endl;
cout << "/*其中数量为无限大时,用0表示*/" << endl;
for (int i = 1; i <= n; i++)
{
cin >> w[i] >> v[i] >> k[i];
}
for (int i = 1; i <= n; i++)
{
//01背包问题
if (1 == k[i])
{
for (int j = C; j >= w[i]; j--)
{
f[j] = max(f[j], f[j - w[i]] + v[i]);
}
}
//完全背包问题
else if (0 == k[i])
{
for (int j = w[i]; j <= C; j++)
{
f[j] = max(f[j], f[j - w[i]] + v[i]);
}
}
//多重背包问题
else
{
for (int j = C; j >= w[i]; j--)
{
for (int l = 1; l < k[i] && l*w[i] <= j; l++)
{
f[j] = max(f[j], f[j - l*w[i]] + l*v[i]);
}
}
}
}
cout << "最大价值为:"<<f[C] << endl;
system("pause");
}
版权声明:本文为weixin_42579072原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。