提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
前言
提示:这里可以添加本文要记录的大概内容:
ESPRIT算法记录
提示:以下是本篇文章正文内容,下面案例可供参考
一、ESPRIT算法什么?
ESPRIT算法是一种基于子空间的角度估计算法
对于均匀线阵模型,显然有
Y
=
A
x
+
n
Y = Ax + n
Y
=
A
x
+
n
其中A是导向矢量构成的矩阵,
A
=
[
a
(
θ
1
)
,
a
(
θ
2
)
.
.
.
,
a
(
θ
k
)
]
A = [a(\theta_1) ,a(\theta_2)…,a(\theta_k)]
A
=
[
a
(
θ
1
)
,
a
(
θ
2
)
…
,
a
(
θ
k
)]
,
a
(
θ
)
=
[
e
i
π
∗
0
∗
s
i
n
(
θ
)
,
.
.
,
e
i
π
∗
(
N
−
1
)
s
i
n
(
θ
)
]
T
a(\theta) = [e^{i\pi*0*sin(\theta)},..,e^{i\pi*(N-1)sin(\theta)}]^T
a
(
θ
)
=
[
e
iπ
∗
0
∗
s
in
(
θ
)
,
..
,
e
iπ
∗
(
N
−
1
)
s
in
(
θ
)
]
T
,其中N为阵元数,k为用户数。
二、ESPRIT算法
1.计算理论协方差矩阵
C
=
E
[
Y
Y
H
]
=
A
P
A
H
+
σ
2
C = E[YY^H] = APA^H+\sigma^2
C
=
E
[
Y
Y
H
]
=
A
P
A
H
+
σ
2
,P为一个对角阵,所以可以得到A构成了信号子空间。
2.旋转不变性
可以看出A具有一些特性,即A的每一行和上面都是成比例的,所以我们有
J
1
A
d
i
a
g
(
e
i
π
∗
Δ
∗
s
i
n
(
θ
l
)
)
l
−
1
k
=
J
2
∗
A
J_1Adiag(e^{i\pi*\Delta*sin(\theta_l)})_{l-1}^{k} = J_2*A
J
1
A
d
ia
g
(
e
iπ
∗
Δ
∗
s
in
(
θ
l
)
)
l
−
1
k
=
J
2
∗
A
,其中
J
1
,
J
2
J_1,J_2
J
1
,
J
2
定义为从N行中取n行,
J
2
J2
J
2
与
J
1
J1
J
1
相差行数为
Δ
\Delta
Δ
,实际上主要是A导向矢量的特性。
实际上如果我们能够估计的很好那么显然
U
s
=
A
∗
Q
Us=A*Q
U
s
=
A
∗
Q
,因为如果估计的很好
U
s
Us
U
s
和
A
A
A
就是一个空间,所以存在一个变换,将两者联立起来,Q是一个满秩矩阵。
所以我们有下面式子
Q
d
i
a
g
(
e
i
π
∗
Δ
∗
s
i
n
(
θ
l
)
)
l
−
1
k
Q
−
1
=
(
J
1
U
s
)
+
J
2
U
s
Qdiag(e^{i\pi*\Delta*sin(\theta_l)})_{l-1}^{k}Q^{-1} = (J_1U_s)^{+}J_2U_s
Q
d
ia
g
(
e
iπ
∗
Δ
∗
s
in
(
θ
l
)
)
l
−
1
k
Q
−
1
=
(
J
1
U
s
)
+
J
2
U
s
其实也就是
d
i
a
g
(
e
i
π
∗
Δ
∗
s
i
n
(
θ
l
)
)
l
−
1
k
diag(e^{i\pi*\Delta*sin(\theta_l)})_{l-1}^{k}
d
ia
g
(
e
iπ
∗
Δ
∗
s
in
(
θ
l
)
)
l
−
1
k
与
(
J
1
U
s
)
+
J
2
U
s
(J_1U_s)^{+}J_2U_s
(
J
1
U
s
)
+
J
2
U
s
,相似,而我们要求的角度就在左边这个矩阵的对角线元素上(其实也就是特征值),而由于相似,我们可以直接去求右边矩阵的特征值,然后通过反变换
θ
=
a
r
c
s
i
n
(
a
r
g
(
λ
(
(
J
1
U
s
)
+
J
2
U
s
)
)
/
(
p
i
∗
Δ
)
)
,
θ= arcsin(arg(λ( (J_1U_s)^{+}J_2U_s))/(pi*\Delta)),
θ
=
a
rcs
in
(
a
r
g
(
λ
((
J
1
U
s
)
+
J
2
U
s
))
/
(
p
i
∗
Δ
))
,
3.Code
%% ESPRIT theory, k =1 error
close all; clear; clc
coeff = 1;
N = 100*coeff;
T = 2*N*coeff;
c= N/T;
p = N;
e = @(index) [zeros(index-1,1);1;zeros(p-index,1)];
% theta_true = -10/180*pi; % should belong to (-pi, pi)
clear i
theta_true = [10];
k = length(theta_true);
A = exp(pi*1i*(0:N-1)'*sind(theta_true))/sqrt(N);
P = diag([1]);
S = 1*randn(k,T);
Z = complex(randn(N,T), randn(N,T))/sqrt(2); %% 噪声功率为1
X = A*S + Z;
SCM = X*(X')/T;
[U,eigs_SCM] = eig(SCM,'vector');
[eigs_SCM, index] = sort(eigs_SCM,'descend');
U = U(:, index);
u_S = U(:,1:k);
J_tmp = eye(N);
n = round(N/2);
Delta = 5;
index = 30;
J1 = J_tmp(index:n+index,:);
J2 = J_tmp(index+Delta:n+index+Delta,:);
test1 = u_S'*(J1'*J2)*u_S;
test2 = u_S'*(J1'*J1)*u_S;
test1_estim = A'*(J1'*J2)*A;
test2_estim = A'*(J1'*J1)*A;
Res = inv(test2_estim) * test1_estim;
[EigenVector,EigenValue] = eig(Res,'vector');
res1 = asind(angle(EigenValue)/pi/Delta)
figure;
plot(res1,0,'.','Color','g','MarkerSize',30)
hold on;
Res = inv(test2) * test1;
[EigenVector,EigenValue] = eig(Res,'vector');
res2 = asind(angle(EigenValue)/pi/Delta)
plot(res2,0,'.','Color','r','MarkerSize',30)
% xline(theta_true,0,'-')
% plot(theta_true,0,'.','Color','b','MarkerSize',30)

给出了协方差矩阵估计正确和误差近似的结果,因为实际上我们只能得到取样协方差矩阵,而不是真正的协方差矩阵,所以我们用
U
~
s
\tilde{U}_s
U
~
s
去替代真实的
U
s
U_s
U
s
,是有误差的,图上给出了误差实例
多角度
%% Estimation of the "direction of arrival" of signal from noisy observations
% MUSIC versus ESPRIT
close all; clear; clc
coeff = 2;
p = 256*coeff;
n = 3*p*coeff;
theta_true = [-10, 35, 37]./180*pi; % should belong to (-pi, pi)
%theta_true = [35, 37]./180*pi; % should belong to (-pi, pi)
%theta_true = [-10, 30]./180*pi; % should belong to (-pi, pi)
k = length(theta_true);
sigma2 = .1;
%P = eye(k);
P = diag([1 3 7]);
clear i
a = @(theta) exp(pi*1i*sin(theta)*(0:p-1)')/sqrt(p);
%a = @(theta) exp(pi*1i*sin(theta)*(0:p-1)');
A = [];
for tmp_index=1:length(theta_true)
A = [A a(theta_true(tmp_index))];
end
%theta_range = linspace(-180,180,500)./180*pi;
theta_range = linspace(-90,90,1000)./180*pi;
S = sqrtm(P)*randn(k,n);
Z = complex(randn(p,n), randn(p,n));
X = A*S + sqrt(sigma2/2)*Z;
SCM = X*(X')/n;
[U,eigs_SCM] = eig(SCM,'vector');
[eigs_SCM, index] = sort(eigs_SCM,'descend');
U = U(:, index);
U_S = U(:,1:k);
J_tmp = eye(p);
n = round(p/8);
J1 = J_tmp(1:n,:);
J2 = J_tmp(2:n+1,:);
test1 = U_S'*(J1'*J2)*U_S;
test2 = U_S'*(J1'*J1)*U_S;
Psi_test = inv(test2) * test1;
[EigenVector,EigenValue] = eig(Psi_test,'vector');
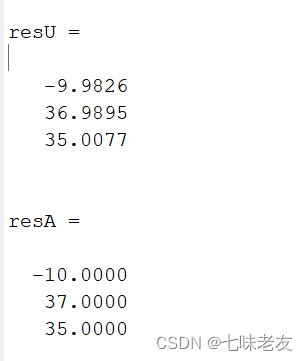
resU = asind(angle(EigenValue)/pi/1)
test1 = A'*(J1'*J2)*A;
test2 = A'*(J1'*J1)*A;
Psi_test = inv(test2) * test1;
[EigenVector,EigenValue] = eig(Psi_test,'vector');
resA = asind(angle(EigenValue)/pi/1)
总结
记录学习过程