博客

1. 题目描述

给定一个二叉树

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

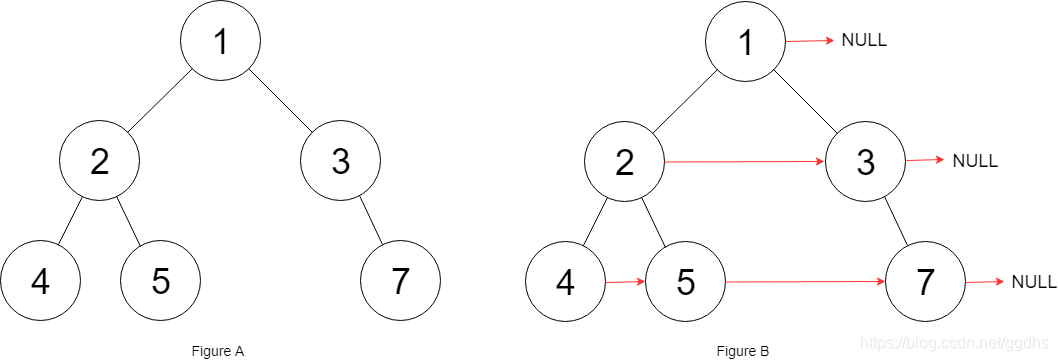
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

你只能使用常量级额外空间。

使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

2. 思路

这个题和上一个题的唯一不同就是树不是完美二叉树。因此需要子节点可能不存在的情况。

2.1 递归

"""
# Definition for a Node.
class Node:
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if root == None:
            return None
        if root.left:
            if root.right:
                root.left.next = root.right
            else:
                root.left.next = self.nextNode(root.next)  
                # 右子树不存在的话，左子树的next就是当前层的最近的那一个节点，
                # 因此这就要求再找当前节点的next时，右边的next的关系必须是完整的，
                # 要不然nextNode(root.next)明明有，但会返回None，会出现错误。
        if root.right:
            root.right.next = self.nextNode(root.next)
        self.connect(root.right)  
        # 注意这里要先递归右子树，因为如果父节点右子树不存在的话，
        # 左子树的next需要找父节点next的子树，
        # 因此必须先把右边的next关系理顺
        self.connect(root.left)
        return root
    def nextNode(self,node):   # 借助一个辅助函数，来寻找离着最近的节点
        if node == None:
            return None
        while node:
            if node.left:
                return node.left
            if node.right:
                return node.right
            node = node.next
        return None

2.2 非递归

队列进行层次遍历仍然是最简单的做法，但是空间复杂度又要求。

队列本质上是维护节点之间的先后顺序，因此可以用这个题目中的next来进行代替。

2.2 非递归代码

"""
# Definition for a Node.
class Node:
    def __init__(self, val, left, right, next):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""
class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if root == None:
            return None
        firstNode = root
        while firstNode:  
            while firstNode and firstNode.left == None and firstNode.right == None:
                firstNode = firstNode.next
                # firstNode是每一层中有子树的第一个节点，而firstNode这一层已经建立好next关系了
            if firstNode == None:
                break
            cur = firstNode
            pre = None   #pre = None  # 类似于链表的头结点
            # pre用来表示当前节点的之前信息，即 pre.next = cur.left(or right)
            while cur:  # 用next代替队列实现当前层节点之间的前后关系。
                if cur.left:
                    if pre:
                        pre.next = cur.left
                    pre = cur.left
                if cur.right:
                    if pre:
                        pre.next = cur.right
                    pre = cur.right
                cur = cur.next
            firstNode = firstNode.left if firstNode.left else firstNode.right
        return root